博弈论与强化学习实战——CFR算法——剪刀石头布
博弈论与强化学习实战——CFR算法——剪刀石头布
感谢：
浅谈德州扑克AI核心算法：CFR - 掘金 (juejin.cn)
虚拟遗憾最小化算法（CFR）基础知识详解 - 知乎 (zhihu.com)
一 游戏介绍
-
有两个参与者，
-
每个参与者有三个可选动作 剪刀石头布 ，分别用0，1，2表示
-
奖励：获胜奖励为1，失败奖励为-1，平局没有奖励，收益矩阵如下
-
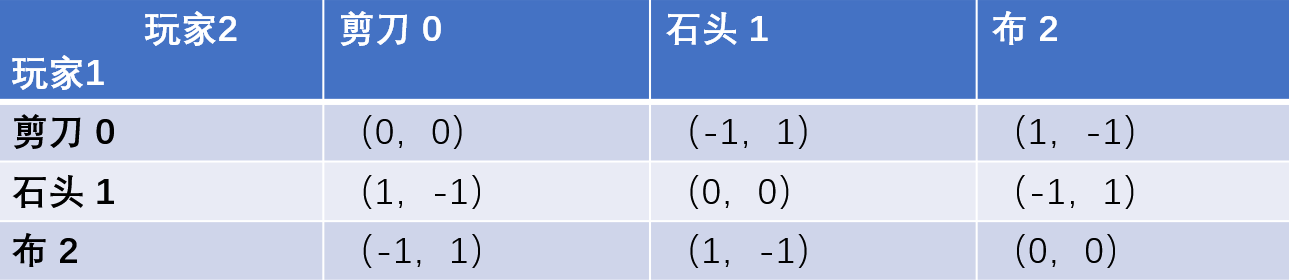
博弈过程用博弈树进行描述：
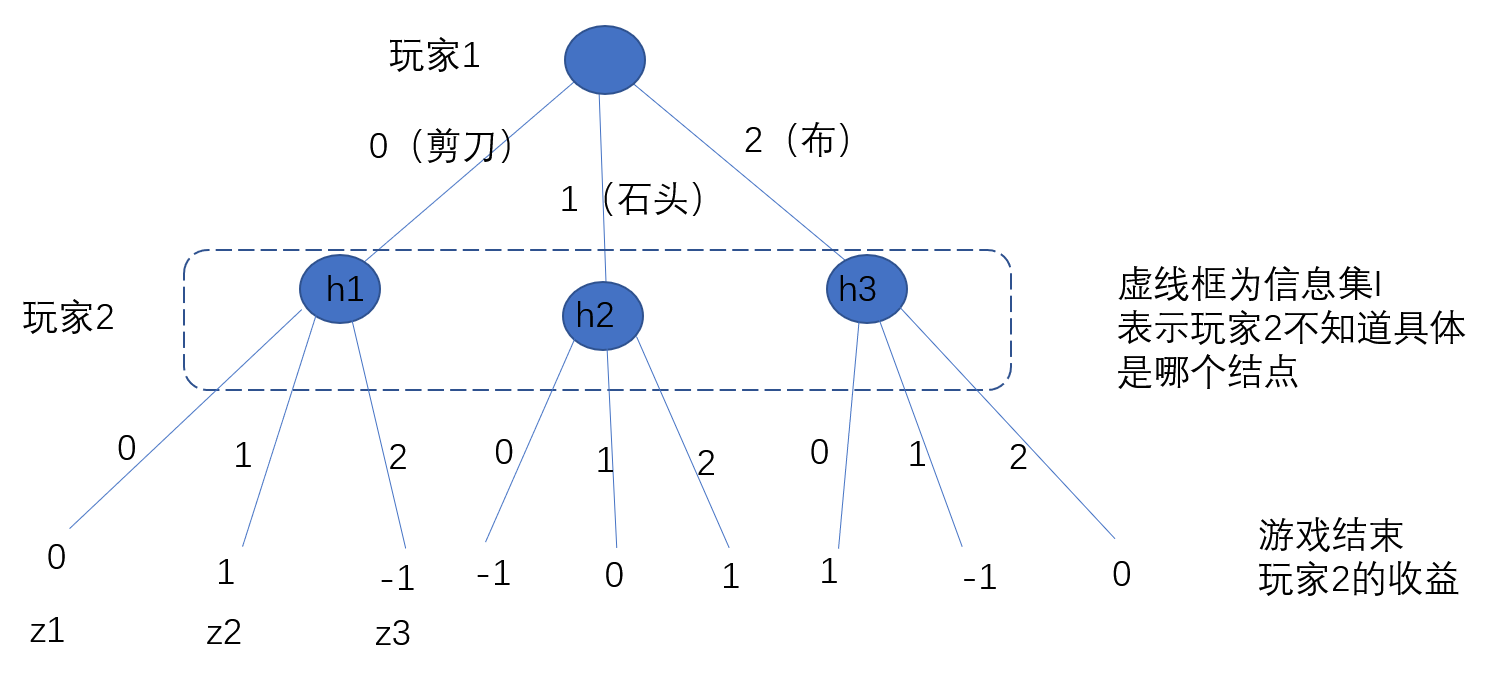
第二个玩家在决策的时候有三个可能的状态\(h1,h2,h3\)，但由于三个状态在同一个信息集中，所以玩家2在决策的时候并不知到具体处于哪个信息集，所以玩家2的决策并不依赖于玩家1的行动结果，从效果上来看就等同于两者同时划拳。
-
玩家的策略即玩家选择三个不同动作的概率，
使用代码将游戏流程
#游戏设置
NUM_ACTIONS = 3 #可选的动作数量
actions = [0,1,2] # 0代表剪刀scissors ， 1代表石头rock ，2 代表布 paper
actions_print=['剪刀','石头','布']
#动作的收益 ，两个人进行博弈，结果
utility_matrix = np.array([
[0,-1,1],
[1,0,-1],
[-1,1,0]
])
"""基本信息初始化"""
# 玩家，初始化
#策略
player1_strategy = np.array([0,0,1])
player2_strategy = np.array([0.4,0.3,0.3])
#动作收益
player1_utility = np.zeros(3)
player2_utility = np.zeros(3)
"""1局游戏的过程"""
print(f'----------------游戏开始-------------------')
# 使用当前策略 选择动作
action_p1 = np.random.choice(actions, p=player1_strategy)
action_p2 = np.random.choice(actions, p=player2_strategy)
print(f'玩家1 动作:{actions_print[action_p1]} ,玩家2 动作:{actions_print[action_p2]} .')
# 得到收益
reward_p1 = utility_matrix[action_p1, action_p2]
reward_p2 = utility_matrix[action_p2, action_p1]
# 输出游戏结果
print(f'----游戏结束-----')
print(f'玩家1 收益{reward_p1} ,玩家2 收益{reward_p2}.')
# 更新玩家的收益
player1_utility[action_p1] += reward_p1
player2_utility[action_p2] += reward_p2
# 输出一局游戏后的动作收益矩阵
print(f'收益更新---------动作:{actions_print[0]} {actions_print[1]} {actions_print[0]}')
print(f'玩家1的累计收益 收益:{player1_utility[0]}; {player1_utility[1]}; {player1_utility[2]} ')
print(f'玩家2的累计收益 收益:{player2_utility[0]}; {player2_utility[1]}; {player2_utility[2]} ')
二 问题引出
假定现在有一个玩家（玩家1）的策略（动作集合上的概率分布）为 0.4，0.3 ，0.3 ，那么玩家2的策略应该是怎样的呢？
方法一 ：求解期望奖励最大的策略
假定玩家2的概率分别为a,b,(1-a-b)
那么其期望收益（奖励乘以发生的概率）为：
要想使得收益最大，结果为\(b=1\),
所以玩家2的策略应为\([0，1，0]\)，此时能够获得的期望奖励为\(0.1\)
方法2 ： 使用CFR算法求解
方法3 ：使用强化学习方法求解
扩展问题：
- 当对战双方都使用相同的算法进行学习，最终结果会不会达到均衡？
- 当双方使用不同的学习算法进行学习，哪个算法达到均衡速度更快？
三 CFR算法求解
1 Regret matching 算法
1 遗憾值的定义
含义： 选择动作a和事实上的策略（概率\(\sigma\)）产生的收益的差别 ,也就是遗憾值(本可以获得更多) ;
遗憾值大于0表示动作\(a\)比当前策略更好，遗憾值小于0表示动作\(a\)不如当前策略
2 Regret matching 算法
上式中 \(R^{T-1}(a)\)表示动作\(a\)的历史遗憾值，然后对其和0取最大值。
和0取最大值目的是要得到累计正的遗憾值，因为只有正的遗憾值对应的动作才是改进的方向。
这个结果就是得到历史遗憾为正的动作，在所有的正的历史遗憾对应的动作计算其分布（也就是概率）然后作为下一次博弈的策略
3 算法流程
Regret matching算法流程为：
-
对于每一位玩家，初始化所有累积遗憾为0。
-
for from 1 to T(T:迭代次数)：
a)使用当前策略与对手博弈
b)根据博弈结果计算动作收益，利用收益计算后悔值
c)历史后悔值累加
d)根据后悔值结果更新策略
-
返回平均策略（累积后悔值/迭代次数）
作者：行者AI
链接：https://juejin.cn/post/7057430423499964424
来源：稀土掘金
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
4 代码实现
完整代码：
# -*- coding: utf-8 -*-
"""
@author : zuti
@software : PyCharm
@file : rock_cfr.py
@time : 2022/11/21 9:26
@desc ：
"""
import numpy as np
#动作设置
NUM_ACTIONS = 3 #可选的动作数量
actions = [0,1,2] # 0代表剪刀scissors ， 1代表石头rock ，2 代表布 paper
actions_print=['剪刀','石头','布']
#动作的收益 ，两个人进行博弈，结果
utility_matrix = np.array([
[0,1,-1],
[-1,0,1],
[1,-1,0]
])
"""基本信息初始化"""
# 玩家，初始化
#策略
player1_strategy = np.array([0.4,0.3,0.3])
player2_strategy = np.array([1/3,1/3,1/3])
#动作收益
player1_utility = np.zeros(3)
player2_utility = np.zeros(3)
#遗憾值
player2_regret = np.zeros(3)
#每一局策略(动作的概率分布)之和
player2_strategy_count = np.zeros(3)
for i in range(10000):
"""1局游戏的过程"""
#对策略进行计数
player2_strategy_count += player2_strategy
print(f'----------------游戏开始-------------------')
# 使用当前策略 选择动作
action_p1 = np.random.choice(actions, p=player1_strategy)
action_p2 = np.random.choice(actions, p=player2_strategy)
print(f'玩家1 动作:{actions_print[action_p1]} ,玩家2 动作:{actions_print[action_p2]} .')
# 得到收益
reward_p1 = utility_matrix[action_p2, action_p1]
reward_p2 = utility_matrix[action_p1, action_p2]
# 输出游戏结果
print(f'----游戏结束-----')
print(f'玩家1 收益{reward_p1} ,玩家2 收益{reward_p2}.')
# 更新玩家的收益
player1_utility[action_p1] += reward_p1
player2_utility[action_p2] += reward_p2
# 输出一局游戏后的动作收益矩阵
print(f'收益更新---------动作:{actions_print[0]} {actions_print[1]} {actions_print[2]}')
print(f'玩家1的累计收益 收益:{player1_utility[0]}; {player1_utility[1]}; {player1_utility[2]} ')
print(f'玩家2的累计收益 收益:{player2_utility[0]}; {player2_utility[1]}; {player2_utility[2]} ')
#
"""遗憾值更新"""
# 根据结果收益计算所有动作的遗憾值
for a in range(3):
# 事后角度 选择别的动作的收益
counterfactual_reward_p2 = utility_matrix[action_p1,a ] # 如果选择动作a(而不是事实上的动作action_p1) ,会获得的收益
regret_p2 = counterfactual_reward_p2 - reward_p2 # 选择动作a和事实上的动作action_p1产生的收益的差别 ,也就是遗憾值(本可以获得更多)
# 更新玩家的动作遗憾值,历史遗憾值累加
player2_regret[a] += regret_p2
print(f'遗憾值更新--------动作:{actions_print[0]} {actions_print[1]} {actions_print[0]}')
print(f'玩家2的累计遗憾值 {player2_regret[0]}; {player2_regret[1]}; {player2_regret[2]} ')
"""根据遗憾值更新策略"""
"""遗憾值归一化"""
# 归一化方法: 1 只看遗憾值大于0的部分，然后计算分布
palyer2_regret_normalisation = np.clip(player2_regret, a_min=0, a_max=None)
print(f'遗憾值归一化')
print(f'玩家1归一化后的累计遗憾值 {palyer2_regret_normalisation [0]}; {palyer2_regret_normalisation [1]}; {palyer2_regret_normalisation [2]} ')
"""根据归一化后的遗憾值产生新的策略"""
palyer2_regret_normalisation_sum = np.sum(palyer2_regret_normalisation) # 求和
if palyer2_regret_normalisation_sum > 0:
player2_strategy = palyer2_regret_normalisation / palyer2_regret_normalisation_sum
else:
player2_strategy = np.array([1 / 3, 1 / 3, 1 / 3]) #否则就采取平均策略
"""最终结果:得到平均策略"""
print(f'-----迭代结束,得到最终的平均策略---------')
#根据累计的策略计算平均策略
average_strategy = [0, 0, 0]
palyer2_strategy_sum = sum(player2_strategy_count)
for a in range(3):
if palyer2_strategy_sum > 0:
average_strategy[a] = player2_strategy_count[a] / palyer2_strategy_sum
else:
average_strategy[a] = 1.0 / 3
print(f'玩家2经过迭代学习得到的平均策略为')
print(f'玩家2的动作 \n 动作:{actions_print[0]} 概率:{average_strategy[0]};动作:{actions_print[1]} 概率:{average_strategy[1]};动作:{actions_print[2]} 概率:{average_strategy[2]} ')
2 CFR算法
1 博弈树中间结点的收益
概念
基于终止状态的收益\(u\)对博弈树中的每个节点都定义一个收益。
最主要的目的是给出博弈树中的中间非叶子结点的收益。
当玩家\(p\)遵循策略\(σ\)时，对于博弈树中任意的一个状态\(h\)，该状态的收益定义为：
式子中，\(u_p(z)\) 按着前面的定义即为 玩家\(p\)到达终止状态\(z\)（叶子节点）所获得的收益；
前面的\(\pi^\sigma(z)\)表示从初始状态出发，当所有玩家都遵循策略\(σ\)时，到达终止状态\(z\)的概率；
求和即表示从初始状态开始把所有包含路径\(h\)到达终点\(z\)的序列进行求和
这个收益即表示 玩家\(p\) 从博弈起点到中间状态\(h\) 再根据策略\(\sigma\)到达终点\(z\)得到的收益。
可以将右端前一项根据概率式1 进行拆分 ，得到
\[\begin{aligned} u_{p}^{\sigma}(h) &=\sum_{z \in Z, h \sqsubset z} \pi^{\sigma}(z) u_{p}(z) \\ &=\sum_{z \in Z, h \sqsubset z} \pi_{p}^{\sigma}(z) \pi_{-p}^{\sigma}(z) u_{p}(z) \ 参与者拆分(1) \\ &=\sum_{z \in Z, h \sqsubset z} \pi^{\sigma}(h) \pi^{\sigma}(z \mid h) u_{p}(z) \ 路径拆分(3) \\ &=\pi_{p}^{\sigma}(h) \sum_{z \in Z, h \sqsubset z} \pi_{-p}^{\sigma}(h) \pi^{\sigma}(z \mid h) u_{p}(z) 参与者+路径拆分(1)+(3) \end{aligned} \]
根据此定义，整局游戏的收益即为博弈树根节点的收益 $ u_{p}{\sigma}=u_{p}(\varnothing) $
当玩家\(p\)遵循策略\(σ\)时，对于博弈树中的一个信息集\(I \in \mathcal{I}\)的收益定义为：
算例
这里给出第二个问题作为一个计算的例子：
玩家\(p\)（为玩家2），其策略\(\sigma\)为\([a,b,1-a-b]\) ,其他玩家\(-p\)（也就是玩家1）的策略\(\sigma\)为\([0.4,0.3,0.3]\)，博弈树见上。
根据上述定义，我们来尝试计算博弈树中间结点\(h1\)的收益
首先，包含中间结点\(h1\)，从游戏开始到达最终结果\(z1,z2,z3\)的路径总共3条。
根据定义式：
第二项：玩家\(p\)玩家2在最终结果的收益分别为
\[u_{p2}(z1)=0 , u_{p2}(z2)= 1, u_{p2}(z3)= -1 \]第一项：从起点出发，经过中间结点\(h1\)，到达最终结果\(z1,z2,z3\)的概率，根据玩家\(p2\)和\(-p\)（也就是玩家1）的策略\(\sigma\)计算为
\[0.4a,0.4b,0.4(1-a-b) \]
概率乘以收益再求和便得到了博弈树中间结点\(h1\)的收益
同样的方法还可以得到博弈树中间结点\(h2,h3\)的收益
信息集\(I\)包含三个结点\(h1,h2,h3\)，因此信息集\(I\)的收益为
理解：信息集\(I\)的收益是基于玩家\(-p\)（玩家1）的策略\(\sigma\) 和 从开始到达最终结点的各条路径。
如果玩家\(p\)（玩家2）想使在信息集\(I\)的收益最大，那么玩家\(p\)（玩家2）的策略（动作集合上的概率）为\([0,1,0]\)，能够获得的期望收益为\(0.1\)
这个结果和我们之前的计算是一致的。由于信息集，所以遍历这个博弈树和矩阵博弈的效果是完全相同的。
2 反事实值
概念
看这个式子的定义：
右端第一项\(\pi_{-p}^{\sigma}(h)\) 表示 其他玩家\(-p\)选择策略\(\sigma\) 从起点到达中间结点\(h\)的概率 ；
第二项\(\pi^{\sigma}(z \mid h)\) 表示路径 经过中间结点\(h\)，然后根据策略\(\sigma\)到达最终结点\(z\)的概率 ，
右端第三项 表示 玩家\(p\)在最终结点\(z\)的收益 ， 然后对所有经过中间结点\(h\)到达最终结点\(z\)的路径进行求和。
结合第2小节中关于\(π\)概率的三个等式，我们可以很容易地推导出状态\(h\)的收益值与反事实值之间的关系：
玩家p在结点\(h\)的期望收益既与其他玩家\(-p\)的策略\(\pi_{-p}^{\sigma}(h)\)和到终点玩家\(p\)的收益\(u_{p}(z)\)，又和玩家p的策略\(\pi_{p}^{\sigma}(h)\)有关。
当终点收益和其他玩家的策略等其他因素是一定的时候，玩家\(p\)在结点\(h\)的期望收益就只与玩家\(p\)的策略有关，这时候把除玩家\(p\)的策略以外的因素（其他玩家的策略和收益的乘积），即不考虑玩家\(p\)的策略影响下玩家\(p\)在结点\(h31\)收益期望 称之为反事实值。
当除玩家\(p\)的策略以外的因素固定的情况下，玩家\(p\)在结点\(h\)的期望收益就只取决于玩家\(p\)的策略，当玩家选定自己的策略想要到达这个状态时候，玩家可以获得一个在这个状态的期望收益，如果玩家\(p\)特别想要到达这个状态，这时候\(\pi_{p}^{\sigma}(h)=1\)，这个时候有两个含义，一当结点\(h\)实在玩家选择动作之前的结点，其含义为是玩家\(p\)的策略不影响这个中间状态期望的收益，二当结点\(h\)实在玩家选择动作之前的结点，其含义为玩家选择策略\(\sigma\)，想要尽力促成这个结果，获得一个在结点\(h\)的收益。
当\(\pi_{p}^{\sigma}(h)=0\)的时候，这时只有结点\(h\)在玩家\(p\)之后才有这个情况，这个时候玩家采取策略\(\sigma\)（动作分布为\([0,a,\cdots,z]\)）的目的是来尽量避免到达中间结点\(h\)。
反事实值实际上就反映了不考虑玩家\(p\)采取策略\(\sigma\)对到达中间结点\(h\)的影响的时候，事实上玩家\(p\)的期望收益。
同样的，将概念扩展到信息集上有 the counterfactual value for player $p $ of an information set \(I \in \mathcal{I}_p\) is
算例
同样给出第二个问题作为一个计算的例子：
玩家\(p2\)（为玩家2），其策略\(\sigma\)为\([a,b,1-a-b]\) ,其他玩家\(-p\)（也就是玩家1）的策略\(\sigma\)为\([0.4,0.3,0.3]\)，博弈树见上。
根据上述定义，我们来尝试计算博弈树中间结点\(h1\)的收益
首先，包含中间结点\(h1\)，从游戏开始到达最终结果\(z1,z2,z3\)的路径总共3条，
根据定义式
右端第一项\(\pi_{-p}^{\sigma}(h)\) 表示 其他玩家\(-p\)（也就是玩家1）选择策略\(\sigma\) 从起点到达中间结点\(h1\)的概率 :
\[\pi_{-p}^{\sigma}(h1) = 0.4 \]第二项\(\pi^{\sigma}(z \mid h)\) 表示路径 经过中间结点\(h\)，然后根据策略\(\sigma\)到达最终结点\(z\)的概率 ;右端第三项 表示 玩家\(p\)（玩家2）在最终结点\(z\)的收益 ;两者相乘表示经过中间结点的收益
\[u_p(z1)=0 , u_p(z2)= 1, u_p(z3)= -1 \\ \pi^{\sigma}(z1 \mid h1) = a,\pi^{\sigma}(z2 \mid h1) =b ,\pi^{\sigma}(z3 \mid h1) = 1-a-b \]
相乘求和就得到了中间结点\(h1\)的反事实值
这里计算出来的反事实值与前面计算出来的收益值相等，而两者其实是有如下关系的
在这里也就是
根据我们的计算又有
所以唯一的解释就是
这里怎么来理解呢：
玩家\(p2\)选择策略\(\sigma\)到达中间结点\(h1\)的概率为1，也就是到达中间结点\(h1\)和玩家\(p2\)的策略无关。这是因为结点\(h1\)是在玩家\(p2\)采取行动之前的结点，所以玩家采取的策略不影响这个结点的期望收益。
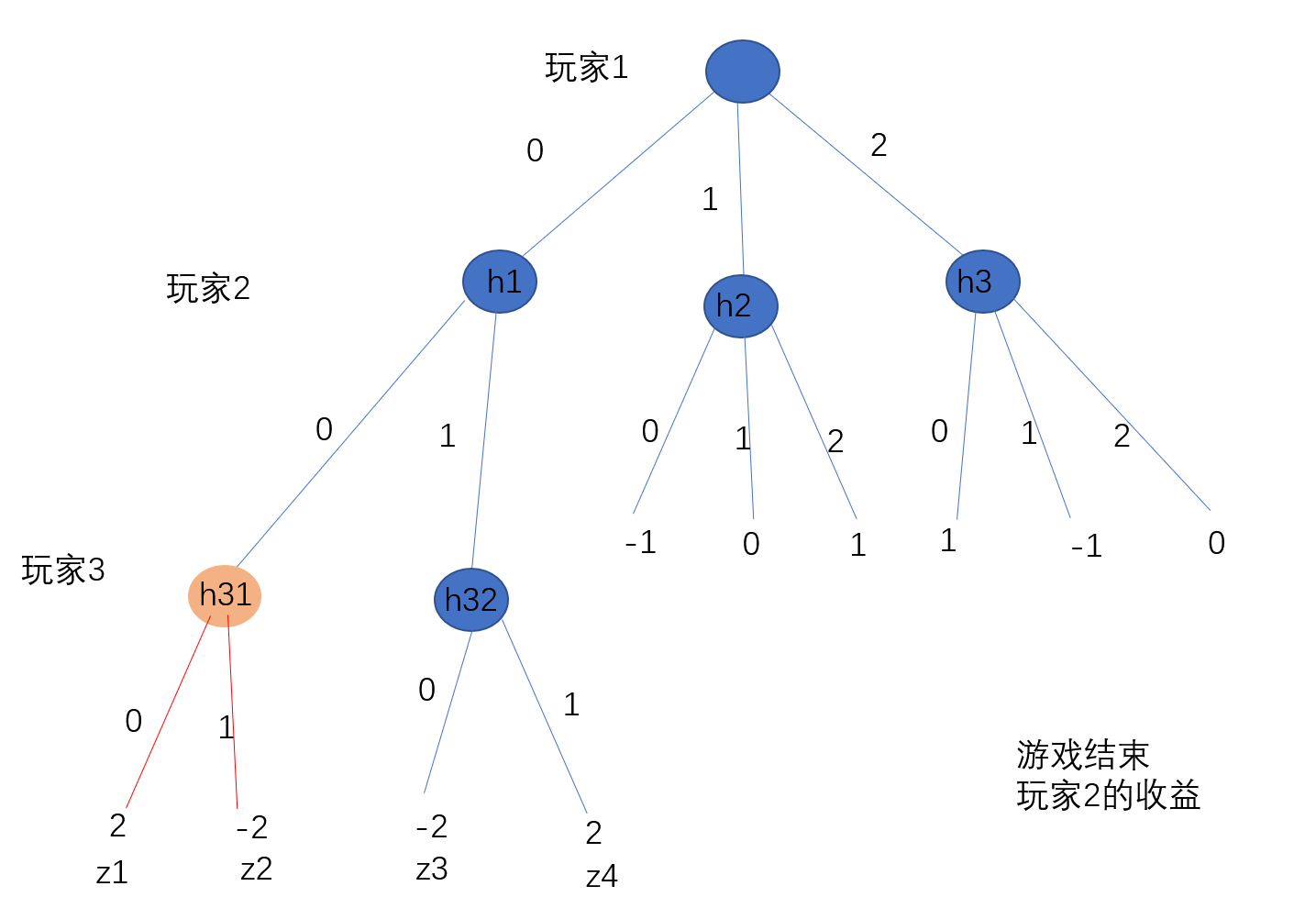
只有当玩家\(p\)的策略选择影响到后续中间结点\(h\)的时候，玩家\(p\)在中间结点\(h\)的收益和玩家\(p\)在中间结点\(h\)的反事实值会有差别，差别就是玩家选择的策略\(\pi^\sigma_p(h)\)（动作概率），选择该动作的概率越小，反事实值越大。下面给出一个示例进行说明.。
博弈树如上图所示，有三个参与者：玩家1，玩家2，玩家3 ，博弈的过程为玩家1，玩家2，玩家3依次行动。
玩家1有三个动作\([0，1，2]\)，其策略（动作概率）为\([0.4,0.3,0.3]\)。玩家2有两个动作，其策略为\([a,1-a]\)。玩家3有两个动作，其策略为\([b,1-b]\)。
可以参照上面的过程来计算玩家2在结点\(h31\)的收益\(u^\sigma_{p2}(h31)\)和反事实值\(v^\sigma_{p2}(h31)\)。
收益计算：把所有从游戏起点经过中间结点\(h31\)的路径的概率乘以收益求和
\[\begin{aligned} u^\sigma_{p2}(h31) &= \sum_{z1,z2} \pi^{\sigma}(z) u_{p2}(z) \\ & = (0.4 \cdot a \cdot b) *r1 +(0.4 \cdot a \cdot 1-b) *r2 \\ \end{aligned} \]反事实值计算：除玩家p2以外的人遵循策略到达中间结点\(h31\)的概率 乘以 从中间结点\(h31\)到结果\(z1,z2\)的不同路径的分布及收益
\[\begin{aligned} v_{p2}^{\sigma}(h31) &= \sum_{z1,z2} \pi_{-p}^{\sigma}(h31) \pi^{\sigma}(z \mid h31) u_{p2}(z) \\ &= 0.4 *b* r1 + 0.4 *1-b * r2 \\ \end{aligned} \]两者的差别就是
\[\pi_{p2}^{\sigma}(h31) = a \\ u^\sigma_{p2}(h31) = a * v_{p2}^{\sigma}(h31) \]当其他玩家的策略和结点收益是既定的时候，后面这一项是事实既定，它不随玩家\(p2\)的策略改变。
当\(p2\)想要到达结点\(h2\)时，它可以提高选择动作\(0\)的比重，即当策略为\([1,0]\)时，玩家\(p2\)在结点\(p2\)的收益为\(1 * v_{p2}^{\sigma}(h31)\)，
当\(p2\)不想要到达结点\(h2\)时，它可以降低选择动作\(0\)的比重，即当策略为\([0,1]\)时，玩家\(p2\)在结点\(p2\)的收益为\(0\)，这个时候也就是由于玩家\(p2\)的策略选择，结点\(h2\)是永远不可能到达的，即这个结点事实上是不存在的。
当玩家\(p2\)的策略和结点的收益是固定的时候，其他玩家的策略选择就决定了玩家\(p2\)在结点\(h31\)的收益。这时侯，反事实值越大，反映其他玩家通过选择策略，想要到达这个结点。反事实值越小，反映其他玩家选择策略，想要尽量避免到达这个结点，其他玩家可以调整策略使得$v_{p2}^{\sigma}(h31) =0 \(，这个时候结点\)h31$就是不存在的。
当玩家2选择动作0的概率a越大，玩家2在中间结点\(h31\)获得的期望奖励值就越大。因为只有到达结点\(h31\)才会有中间这个结点的奖励，如果不到达结点\(h31\)（此时，动作a的概率为0），那么自然玩家2在结点\(h31\)就不会有收益。
玩家p2在结点\(h31\)的期望收益既与其他玩家的策略和终点收益，又和玩家p2的策略有关。当其他因素是一定的时候，就只与玩家p2的策略有关，把从其他玩家的策略和收益的乘积即不考虑\(p2\)的策略影响下结点\(h31\)收益期望 称之为反事实值。
把结点收益固定，那么玩家\(p2\)选择动作0的概率（也就是玩家2的策略）会影响反事实值的大小。
\(a\)越大，反事实值越小。如果\(a\)是1，此时反事实值和收益相等，就说明此时玩家2的动作是固定的或者玩家2的策略不影响状态\(h2\)出现的概率，这个时候说明玩家2采取策略\(\sigma=[1,0]\)一定能够到达状态\(h31\)。
\(a\)越小，反事实值越大。如果\(a\)是0.0001，此时反事实值比上述情况大得多，说明当玩家2采取策略\(\sigma=[0.0001,0.9999]\)时，能够到达状态\(h31\)的可能性很小。
反事实值\(v_{p2}^{\sigma}(h31)\)就说明了玩家\(p2\)选择策略\(\sigma\)对到达状态\(h31\)的可能性，反事实值越大，说明在玩家2使用策略\(\sigma\)时越不可能到达状态\(h31\) ，当反事实值与收益相等的时候就说明玩家\(p2\)选择策略\(\sigma\)不影响到达状态\(h31\)的可能性或者所选择的策略能够一定到达状态\(h31\)。
3 反事实遗憾
概念
其定义是基于某个信息集\(I\)和在这个信息集上的特定动作来定义的。
右端后面一项，是对在该信息集上动作期望遗憾值的累和，右端第一项选取该动作的遗憾值。
算例
同样给出第二个问题作为一个计算的例子：
玩家\(p2\)（为玩家2），其策略\(\sigma\)为\([a,b,1-a-b]\) ,其他玩家\(-p\)（也就是玩家1）的策略\(\sigma\)为\([0.4,0.3,0.3]\)，博弈树见上。
根据上述定义，我们来尝试计算博弈树在第一次迭代时候，玩家\(p2\)在信息集\(I=\{h1,h2,h3\}\)采取动作\(a=0\)的反事实遗憾\(R^1(I,a)\)
由于是第一次迭代，没有历史信息
首先计算反事实收益
同样还可以得到
在信息集\(I\)上选择动作\(0,1,2\)的概率分别为
因此在信息集\(I\)上的期望反事实值为
经过上述计算我们会发现此时计算出来的玩家\(p2\)在信息集\(I\)上的期望反事实值和在第一部分计算出来的信息集\(I\)上玩家\(p2\)的期望收益是一样的。其原因就是信息集\(I\)的出现并不依赖于玩家\(p2\)的动作。
反事实遗憾为
因此。第一次迭代时，玩家\(p2\)在信息集\(I\)上采取动作\(0\)的反事实遗憾为\(- (0.1a+0.2b-0.1)\)
4 原始CFR算法
算法步骤：
-
Generate strategy profile σt from the regrets, as described above.
根据regret-matching算法计算本次博弈的策略组
For all $ I \in \mathcal{I}, a \in A(I) $, and $ p=p(I) $:
\[\sigma_{p}^{t}(I, a)=\left\{\begin{array}{ll}R^{t}(I, a)^{+} / \sum_{b \in A(I)} R^{t}(I, b)^{+} & \sum_{b \in A(I)} R^{t}(I, b)^{+}>0 \\ \frac{1}{|A(I)|} & \text { otherwise }\end{array}\right. \]因为动作\(a\)的遗憾值为正表示该动作正确，在下次迭代中无需更改，体现了遗憾匹配算法“有错就改，无错不改”的特点。
其中如果所有动作的遗憾值为0，则在下次迭代中采取每一种动作的概率相同。
-
Update the average strategy profile to include the new strategy profile.
使用上一步中新计算的策略组更新平均策略组
For all $ I \in \mathcal{I}, a \in A(I) $, and $ p=p(I) $:
\[\begin{aligned} \bar{\sigma}_{p}^{t}(I, a) &=\frac{1}{t} \sum_{t^{\prime}=1}^{t} \pi_{p}^{\sigma^{t}}(I) \sigma_{p}^{t^{\prime}}(I, a) \\ &=\frac{t-1}{t} \bar{\sigma}_{p}^{t-1}(I, a)+\frac{1}{t} \pi_{p}^{\sigma^{t}}(I) \sigma_{p}^{t}(I, a) \end{aligned} \]上式表示玩家\(p\)的平均策略\(\bar{\sigma}_{p}^{t}(I, a)\)，即为前\(t\)次的即时策略的平均值
-
Using the new strategy profile, compute counterfactual values.
使用第一步计算的新策略组计算双方参与者的反事实收益值
For all $ I \in \mathcal{I}, a \in A(I) $, and $ p=p(I) $:
\[\begin{aligned} v_{p}^{\sigma^{t}}(I, a) &=\sum_{h \in I \cdot a} v_{p}^{\sigma^{t}}(h) \\ &=\sum_{h \in I \cdot a} \sum_{z \in Z, h \sqsubset z} \pi_{-p}^{\sigma^{t}}(h) \pi^{\sigma^{t}}(z \mid h) u_{p}(z) \end{aligned} \] -
Update the regrets using the new counterfactual values.
使用反事实收益值更新遗憾值
For all $ I \in \mathcal{I}, a \in A(I) $, and $ p=p(I) $:
\[R^{t}(I, a)=R^{t-1}(I, a)+v_{p}^{\sigma^{t}}(I, a)-\sum_{a \in A(I)} \sigma^{t}(I, a) v_{p}^{\sigma^{t}}(I, a) \]
-
对于每一位玩家，初始化反事实遗憾值\(R^t(I,a)\)为0 平均策略\(\bar{\sigma}_p(I,a)\)为0 ，初始化策略为随机策略
-
for from 1 to T(T:迭代次数)：
a) 根据regret-matching算法计算本次博弈的策略组\(\sigma_p^t(I,a)\)
a)使用当前策略更新平均策略\(\bar{\sigma}^t_p(I,a)\)
c)计算反事实收益值\(v^{\sigma^t}_p(I,a)\)
d) 使用反事实收益值计算遗憾值\(R^t(I,a)\)
-
返回平均策略（累积后悔值/迭代次数）
伪代码：
算法分析：
通过上述算法步骤我们可以得到：
对于每个信息集\(I\)和动作\(a\) , \(R\)和\(\bar{\sigma}\)都相当于一个历史列表，存储了过去迭代过程中的累计遗憾值和累计平均策略 。 \(\sigma\)和\(v\)是临时列表，用来存储当前的策略和反事实值。
值得注意的是，虽然 CFR 处理的都是行为策略（即在每个信息集上动作的概率分布），但求平均策略的过程，是在混合策略或序列形式策略的空间中进行的。使用序列形式进行描述， 维持一个玩家\(p\)的平均策略， 是通过在每个信息集\(I \in \mathcal{I}\)和动作\(a \in A(I)\)上 增量地更新$ \bar{\sigma}{p}(I, a)=\sum^{T} \pi_{p}^{t}(I) \sigma^{t}(I, a) $完成的。这里，我们忽略了上面给出的算法步骤第二种把和转化为平均的形式，这是因为在将序列形式的策略转化为行为形式的策略 其实是涉及到了 在每个信息集上的概率的正则化。
通过在博弈树的状态深度优先遍历中结合策略计算、平均策略更新和价值计算，可以提高 CFR 的实现效率。算法在下一部分
代码实现
# -*- coding: utf-8 -*-
"""
@author : zuti
@software : PyCharm
@file : rockpaperscissors_cfr_1.py
@time : 2022/11/24 15:51
@desc ：
尝试使用CFR算法来实现剪刀石头布游戏
第一次尝试，使用算法流程进行
"""
import numpy as np
"""游戏设置"""
# 动作设置
NUM_ACTIONS = 3 # 可选的动作数量
actions = [0, 1, 2] # 0代表剪刀scissors ， 1代表石头rock ，2 代表布 paper
actions_print = ['剪刀', '石头', '布']
# 动作的收益 ，两个人进行博弈，结果
utility_matrix = np.array([
[0, 1, -1],
[-1, 0, 1],
[1, -1, 0]
])
""" 游戏基本情况"""
# 玩家1 策略固定 [0.4,0.3,0.3]
# 玩家2，初始化策略为随机策略[1/3,1/3,1/3],的目的是通过CFR算法，学习得到一个能够获得最大收益的策略
# 整个游戏只有一个信息集，其中包含三个结点，在这个信息集合上可选的动作有3个
# 玩家，初始化
# 策略
player1_strategy = np.array([0.4, 0.3, 0.3])
player2_strategy = np.array([1 / 3, 1 / 3, 1 / 3])
# 玩家2在信息集I上关于三个动作的累计的遗憾值
player2_regret_Information = np.zeros(NUM_ACTIONS)
# 玩家2在信息集I上关于三个动作的累计的平均策略
player2_average_strategy = np.zeros(NUM_ACTIONS)
def RegretToStrategy(regret):
"""
使用遗憾值匹配算法 ，根据累计的遗憾值，来确定新的策略
:return: 新的策略 strategy
"""
# 归一化方法: 1 只看遗憾值大于0的部分，然后计算分布
regret_normalisation = np.clip(regret, a_min=0, a_max=None)
#print(f'归一化后的累计遗憾值 {regret_normalisation[0]}; {regret_normalisation[1]}; {regret_normalisation[2]} ')
"""根据归一化后的遗憾值产生新的策略"""
regret_normalisation_sum = np.sum(regret_normalisation) # 求和
strategy = np.zeros( NUM_ACTIONS)
if regret_normalisation_sum > 0:
strategy = regret_normalisation / regret_normalisation_sum
else:
strategy = np.array([1 / 3, 1 / 3, 1 / 3]) # 否则就采取平均策略
return strategy
def UpdateAverage(strategy , average_strategy ,count ):
"""
根据本次计算出来的策略，更新平均策略
进行历史累计，然后对迭代次数进行平均
:param strategy:
:param average_strategy:
:return:
"""
average_strategy_new = np.zeros( NUM_ACTIONS)
#不管玩家p2选择哪个动作，信息集I 的出现概率为 1
for i in range(NUM_ACTIONS):
average_strategy_new[i] = (count -1) / count * average_strategy[i] + 1/count * 1 * strategy[i]
return average_strategy_new
def StrategyToValues(strategy):
"""
计算反事实收益值 v
:param strategy:
:return:
"""
#首先计算信息集I上所有动作的反事实收益 ，见第三节算例
#计算每个动作的反事实收益
counterfactual_value_action = np.zeros(NUM_ACTIONS)
for i in range(NUM_ACTIONS) :
counterfactual_h1 = player1_strategy[0] * 1 * utility_matrix[0][i]
counterfactual_h2 = player1_strategy[1] * 1 * utility_matrix[1][i]
counterfactual_h3 = player1_strategy[2] * 1 * utility_matrix[2][i]
counterfactual_value_action[i] = counterfactual_h1 + counterfactual_h2 +counterfactual_h3
return counterfactual_value_action
def UpdateRegret( regret , strategy , counterfactual_value_action):
"""
更新累计反事实遗憾
:param regret:
:param strategy:
:param counterfactual_value_action:
:return:
"""
# 每个动作的反事实值 乘以 策略（每一个动作的概率） 求和 得到 期望
counterfactual_value_expect = np.sum(counterfactual_value_action * strategy)
for i in range(NUM_ACTIONS):
regret[i] = regret[i] + counterfactual_value_action[i] - counterfactual_value_expect
return regret
def NormaliseAverage(average_strategy):
"""
归一化得到最后结果
:param average_strategy:
:return:
"""
strategy_sum = sum(average_strategy)
strategy = np.zeros(NUM_ACTIONS)
for i in range( NUM_ACTIONS):
strategy[i] = average_strategy[i] / strategy_sum
return strategy
#使用CFR求
for count in range(10):
print(f'玩家2 当前策略 ：{player2_strategy}')
#2 根据当前策略，更新平均策略
player2_average_strategy = UpdateAverage(player2_strategy , player2_average_strategy ,count+1 )
print(f'累计平均策略 ：{player2_average_strategy}')
# 3 根据当前策略计算反事实收益
player2_counterfactual_value_action = StrategyToValues(player2_strategy)
print(f'当前策略对应的反事实收益 ：{player2_counterfactual_value_action}')
#4 更新累计反事实遗憾
player2_regret_Information = UpdateRegret(player2_regret_Information, player2_strategy, player2_counterfactual_value_action)
print(f'累计反事实遗憾 ：{player2_regret_Information}')
# 1 用遗憾值匹配算法 ，根据累计的遗憾值，来确定新的策略
player2_strategy = RegretToStrategy(player2_regret_Information)
print(f'-------------迭代次数{count+1}------------')
result = NormaliseAverage(player2_average_strategy)
print(f'最终结果：{result}')
本文来自博客园，作者：{珇逖}，转载请注明原文链接：https://www.cnblogs.com/zuti666/p/16955436.html
