博弈论与强化学习——基础1 扩展型博弈
博弈论与强化学习——基础1 扩展型博弈
表示形式—— 博弈树
使用树状图来表示行动的次序和执行动作时的信息状态
-
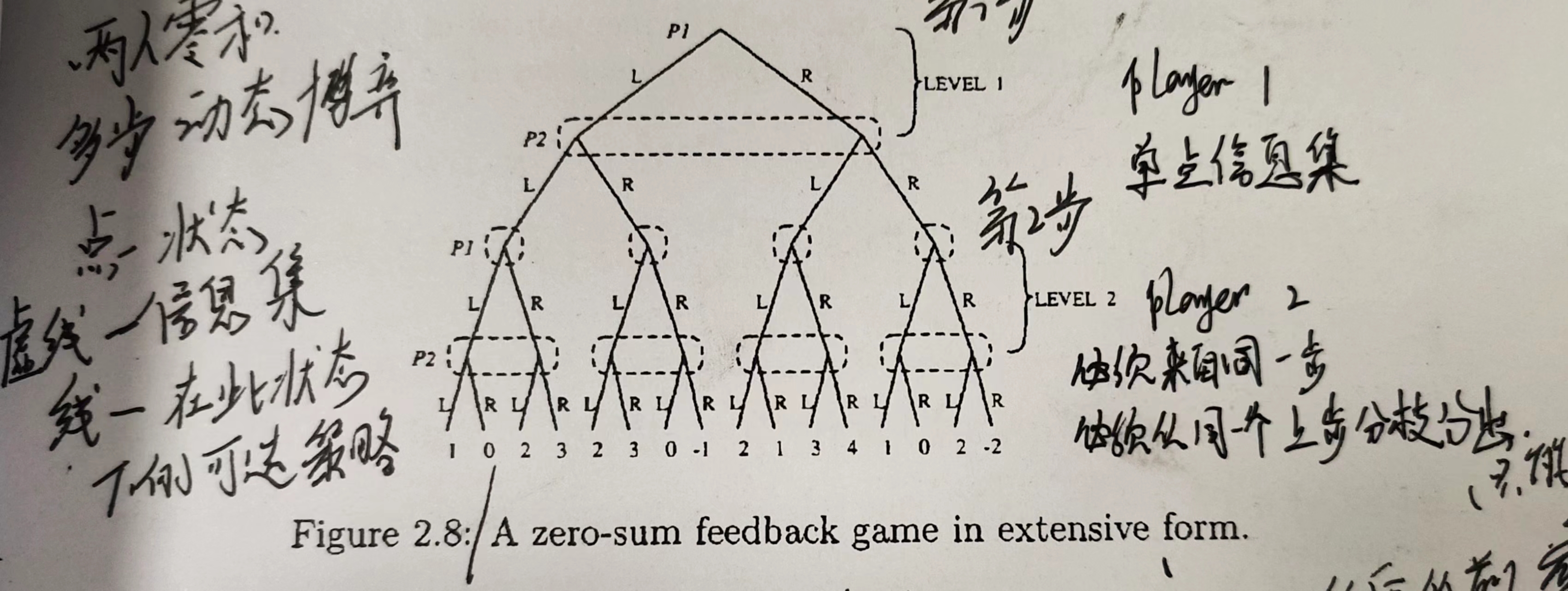
图中有两个参与者 ,进行了两个阶段的博弈
-
结点:表示博弈的状态,
- 根节点:博弈的起点,玩家进行决策。关于博弈怎么开始,博弈的顺序,可以有预定的顺序也可以通过掷色子、投硬币决定等。
- 非叶子结点:决策结点:表示这个时候哪个博弈玩家做出决策。****
- 叶子结点:代表每个玩家在此时的收益。收益只存在于叶子结点
-
虚线框:信息集 ,同一信息集下可以执行的策略是一致的
-
实线、边:在此信息集下可以选择的策略,同一信息集下可以执行的策略是一致的
-
路径:从根结点到当前决策结点的路径中经过的决策的序列(有序集)
信息集 information set
以上虚线框就代表一个信息集。简单来说,虚线框下面的人不知道虚线框里的信息。也就是下一个玩家并不知道前一个玩家干了啥
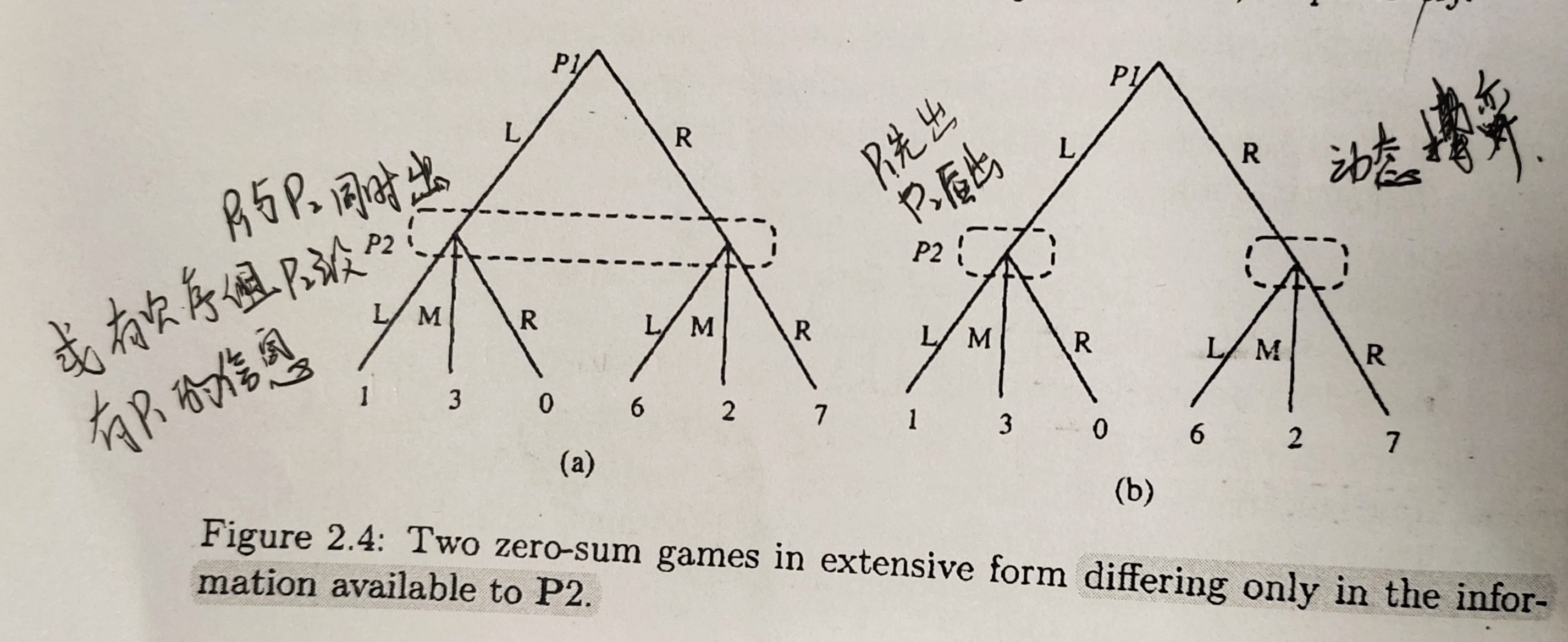
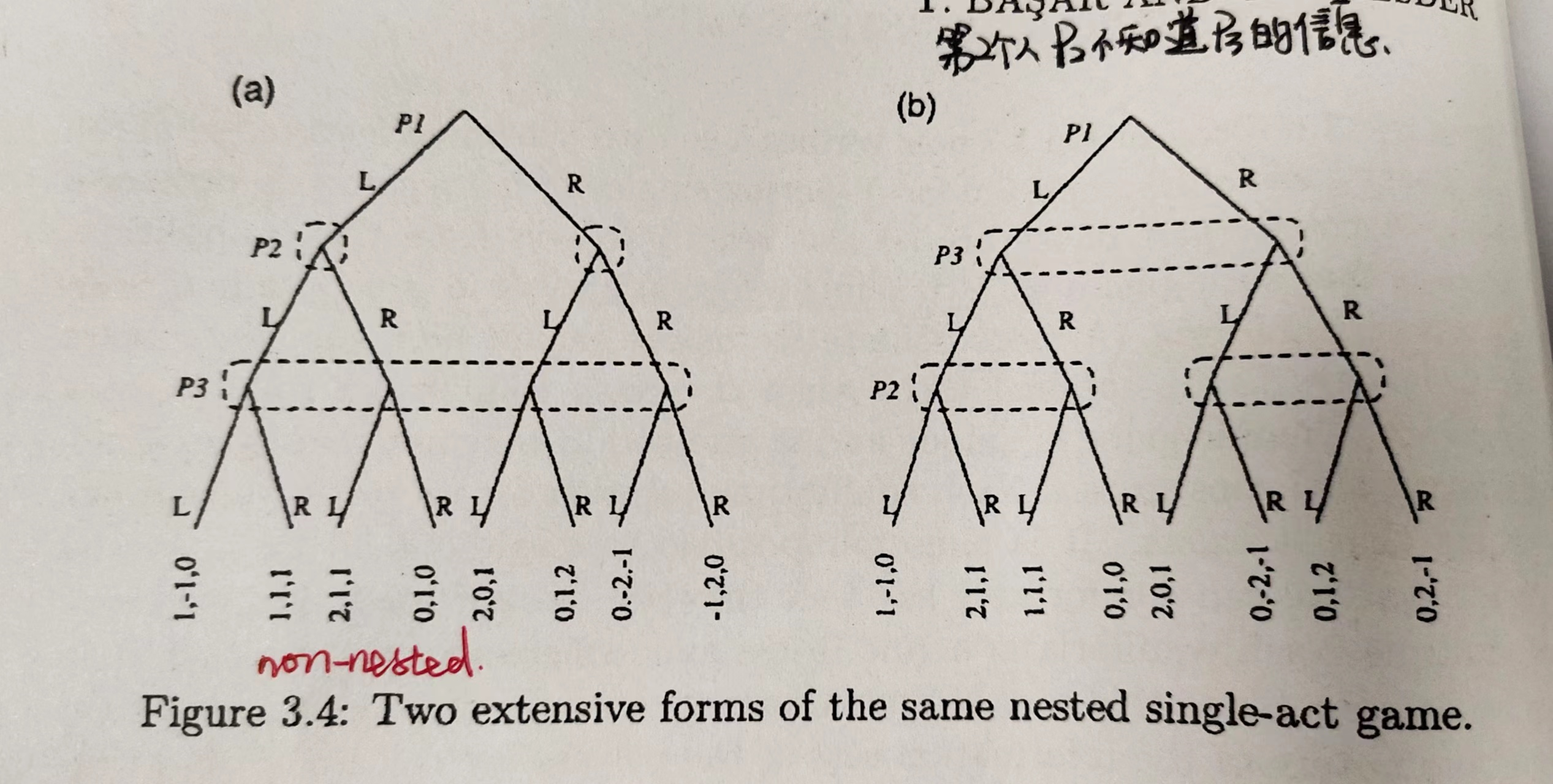
上图是一个二人单步行动的博弈。玩家P1 有两个可选行动,玩家P2有三个可选行动。P1先执行动作,P2后执行动作。收益是零和的,表示P2的收益,也就是P1的损失。
上图a和b的区别就只有信息集的不同。在图a中,P2的两个决策结点在同一个虚线框中,表示P2在决策的时候并不知道P1选择的动作及结果,即P2在决策并没有获得额外信息。 在图b中,P2的决策结点在不同的虚线框中,因此P2观察到了P1选择了哪个行动,也就是从根节点到当前决策结点的路径是P2所知道的,此时P2有着完美信息。
完美信息与不完美信息
上图b清楚地表示了参与者1先动,参与者2观察到参与者1的行动。然而,有些博弈并不是这样,如图a所示,参与者并不是一直能观察到另一 个人的选择(例如,同时行动或者行动被隐藏)。
信息集是决策节点的组合:
1、每个节点都属于一个参与者。
2、参与无法区分信息集里的多个节点。也就是说:如果信息集有多个节点,信息集所属的参与者就不知道能往哪个节点移动。
完美信息的博弈是指在博弈的任何阶段,每个参与者都清楚博弈之前发生的所有行动,也即每个信息集都是一个单元素集合。 没有完美信息的博弈就是不完美信息博弈。
博弈树的公理化表述:

扩展性博弈研究范围的逐步扩展
二人零和单步 —— 二人非零和单步——多人非零和单步
二人零和多步——二人非零和多步——多人非零和多步
-
参与者:二——多
-
行动:单步——多步,有限——无限
-
收益:零和——非零和
有限二人零和多步动态博弈
有限: 时间序列上有限 ,有中止结点
二人:两个参与者
零和:收益和为0
多步:多次采取行动
动态:有着信息集的概念,所谓的动态博弈,就体现在信息集的不唯一
1 feedback
图示
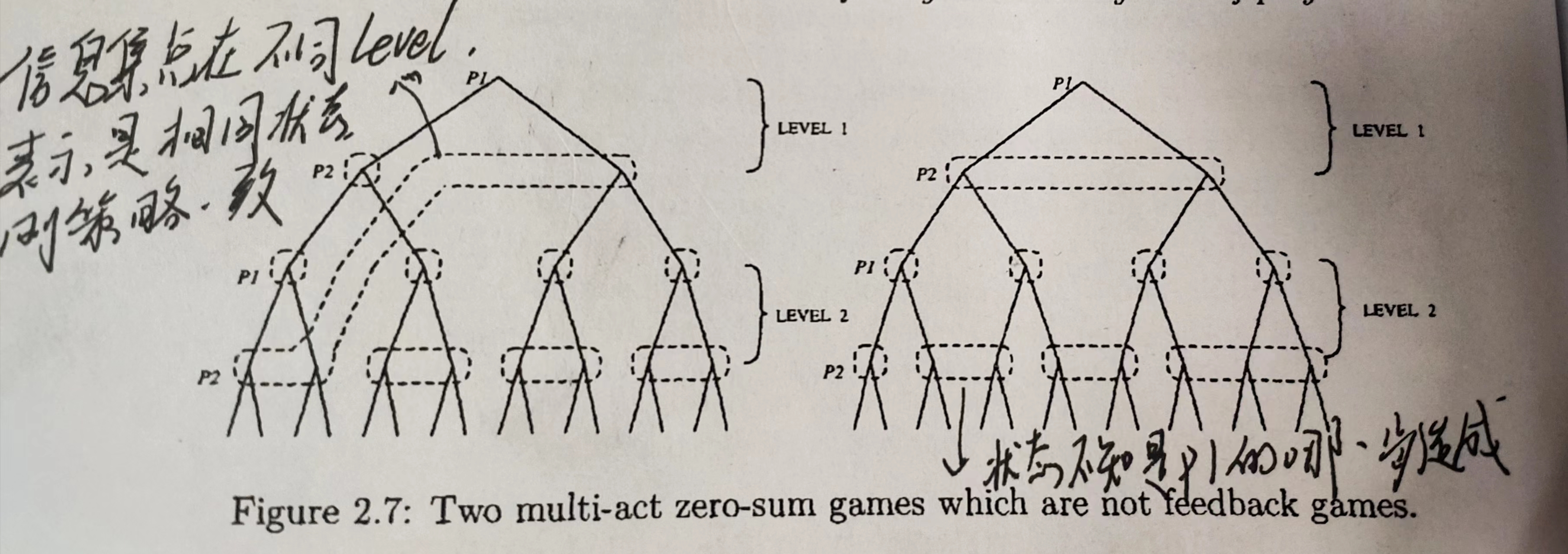
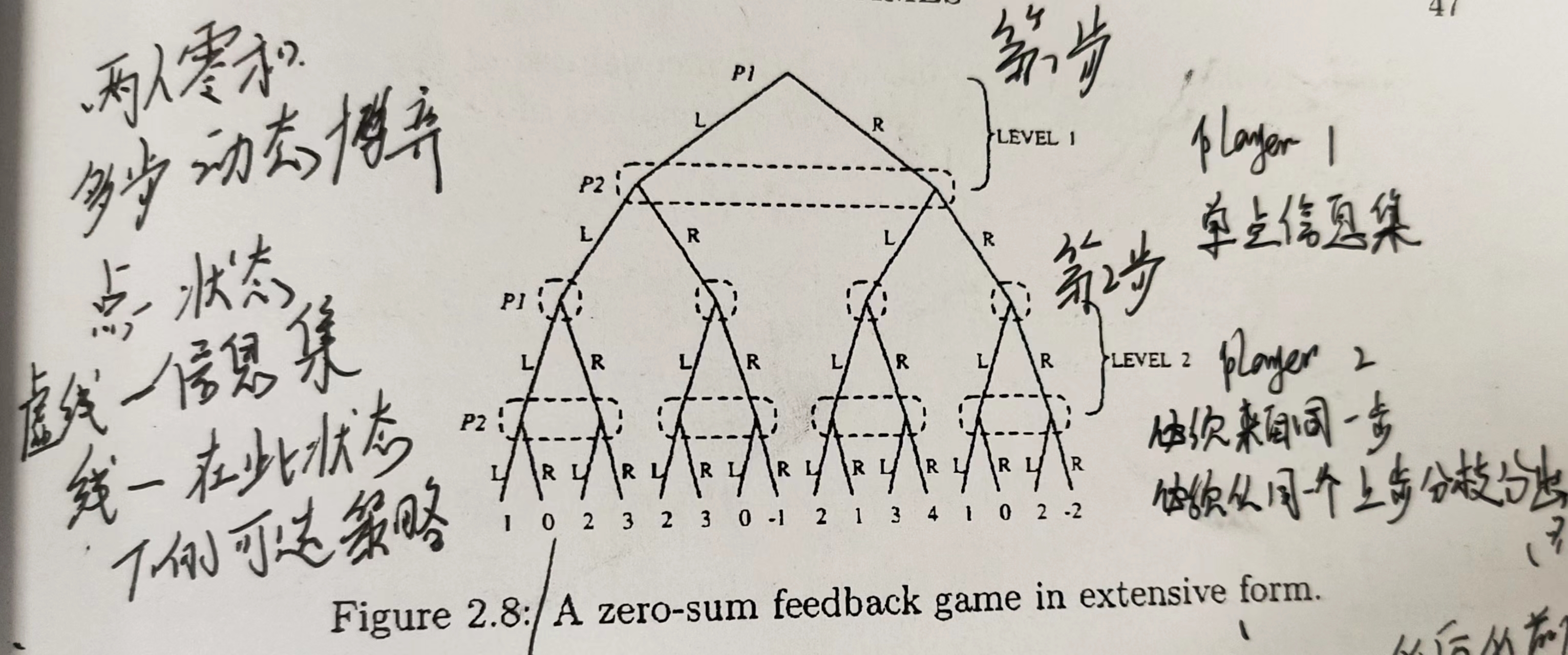
如上图2.8 所示的博弈为二人零和 feed back 博弈,需要满足两个条件:
-
每个参与者都有当前博弈阶段的完美信息。
从图中来看就是信息集都在同一层级,不会出现图2.7左边信息集跨越不同博弈阶段的情况;
-
每个阶段的博弈,后一玩家得信息集的结点不能来自前一玩家不同信息集结点的分支。
从图中来看就是,后面的信息集是从前一玩家的单个信息集延申出来的,如同图2.8所示,而不是2.7右边产生交叉的样子。
所以形如2.8所示的博弈树就是feedback型博弈,这样定义的目的是在之后的剪枝操作能够完全落下去。
求解saddle point 的方法
从最后的叶子结点,也就是最后一层开始,求解这一单步策略交互的 鞍点均衡策略 ,计算收益值。将这一步的博弈剪枝操作,剪下来,用计算的均衡收益替换掉这个博弈树。
也就是将k步的博弈转换为k个1步的博弈。
2 openloop
图示
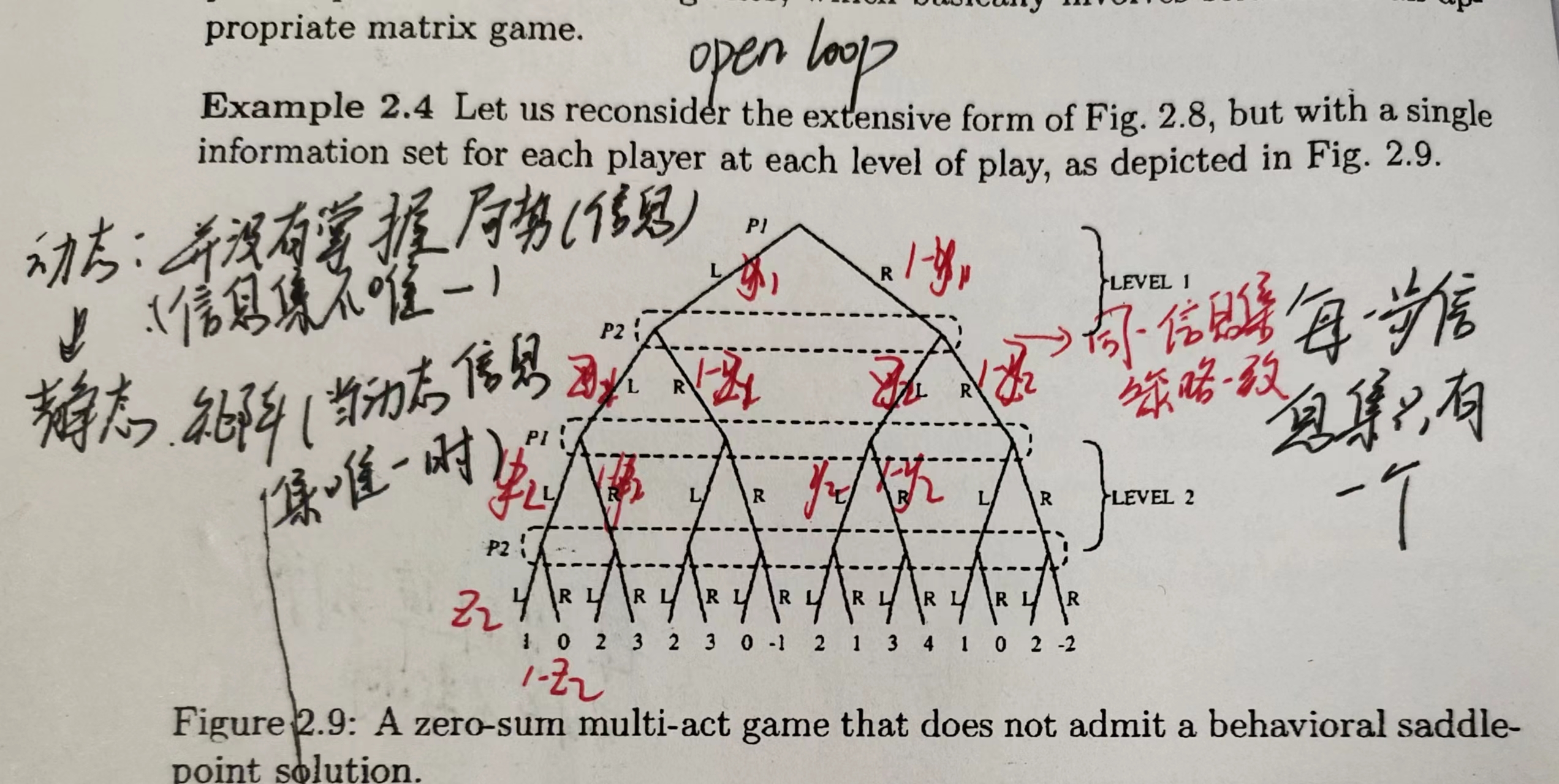
如上图所示,在博弈的每个阶段,所有决策结点都在同一个信息集中,这是一个完全的不完美信息博弈,也就是博弈的任何阶段,每个参与者都不清楚博弈之前发生的行动,这个时候也就没有任何额外的信息,其效果相当于一个静态博弈。
这种对于每个参与者每个阶段都只有一个信息集的博弈称之为 openloop型的扩展性博弈。
求解方法
由于信息集没有提供任何额外信息,其决策效果等同于博弈,所以可以将其多阶段的决策进行组合转换为一个单阶段的静态博弈。
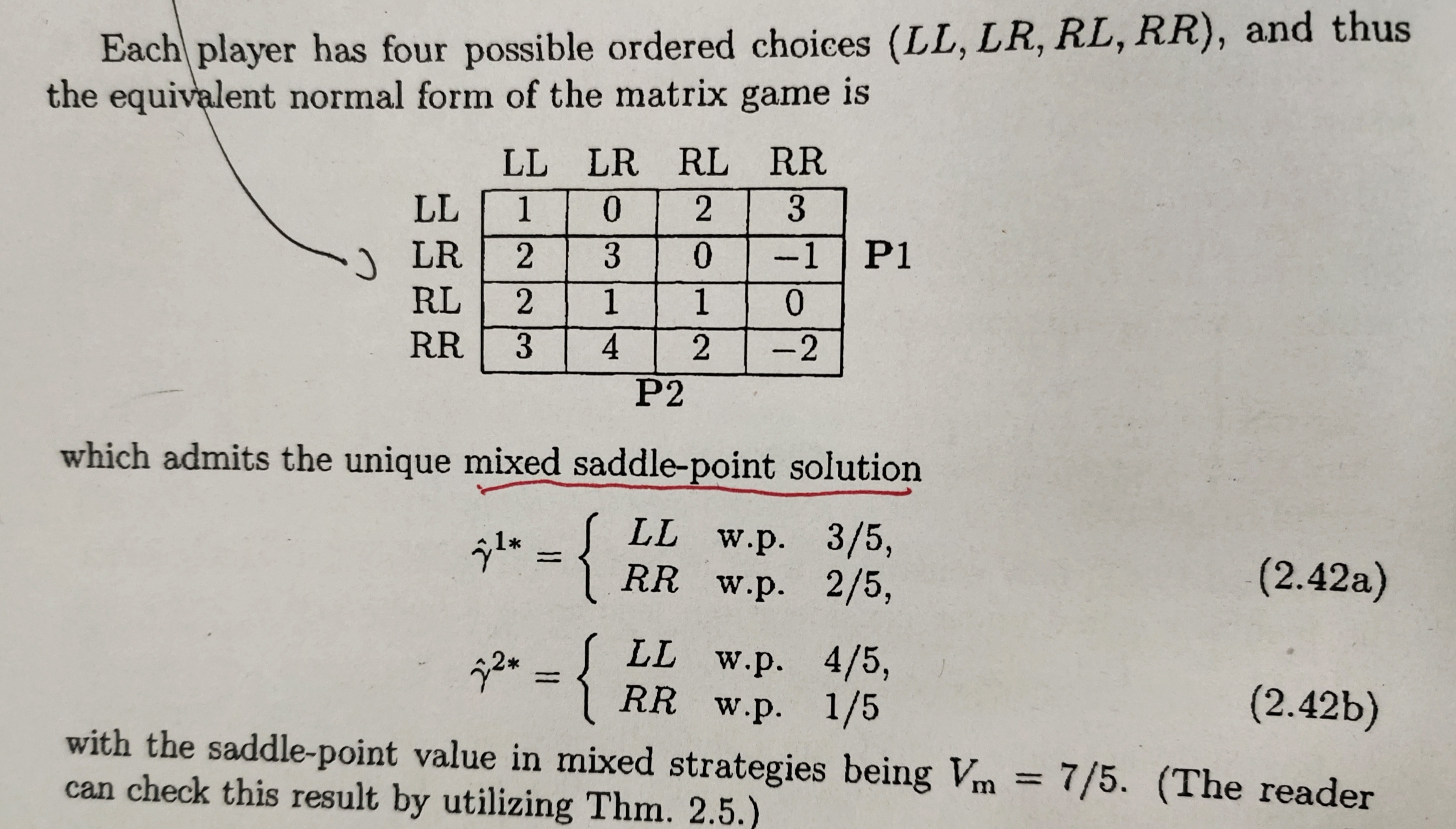
如将上图的openloop型博弈进行转换得到的标准型博弈矩阵如下,然后再求解其鞍点即可。
N 人博弈
定义 Definition 3.10 extensive form tree structure
Definition 3.10 An extensive form of an N-person nonzero-sum finite game without chan moves is a tree structure with
- a specific vertex indicating the starting point of the game
- cost functions , each one assigning a real number to each terminal vertex of the tree,where the th cost dunction determines the loss to be incurred to 。
- a partition of the nodes of the tree into player sets
- a subpartition of each player set into information sets ,such that the same number of branches emanates from every node belonging to the same information set and no node follows another node in the same information set .
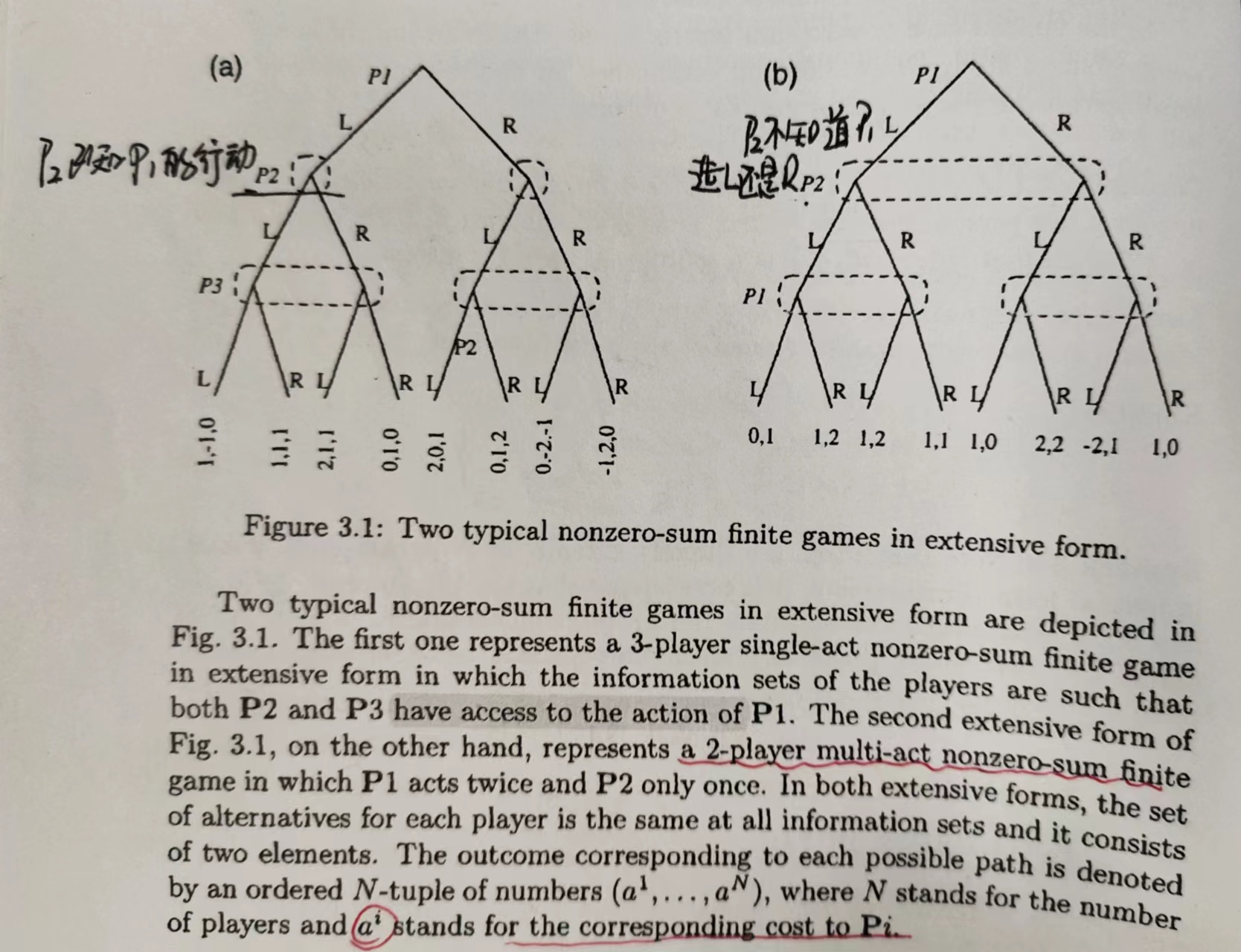
图示 Figure3.1
Two typical nonzero-sum finite games in extensive form are depicted in Fig. 3.1.
The first one represents a 3-player single act nonzero sum finite game in extensive form in which the information sets of the players are such that both P2 and P3 have access to the action of P1.
左边的图是三人单步博弈,P2,P3在决策结点都知道P1所采取的行动,但P3在决策的时候只知道P1的行动而并不知道P2的决策内容
The second extensive form of Fig. 3.1, on the other hand, represents a 2-player multi-act nonzero-sum fnite game in which P1 acts twice and P2 only once.
右边的图是二人多步博弈,其中P1有两次行动。在P2进行决策的时候并不知道P1的行动,P1第二次进行决策时知道自己第一步的行动但不知道P2的行动。
In both extensive formns, theset of alternatives for each player is the same at all information sets and it consise of two elements.
The outcome corresponding to each possible path is denotes by an ordered N-tuple of numbers , wherestands for the number of players and a' stands for the corresponding cost to .
单步博弈
图示 Figure3.2 3.3
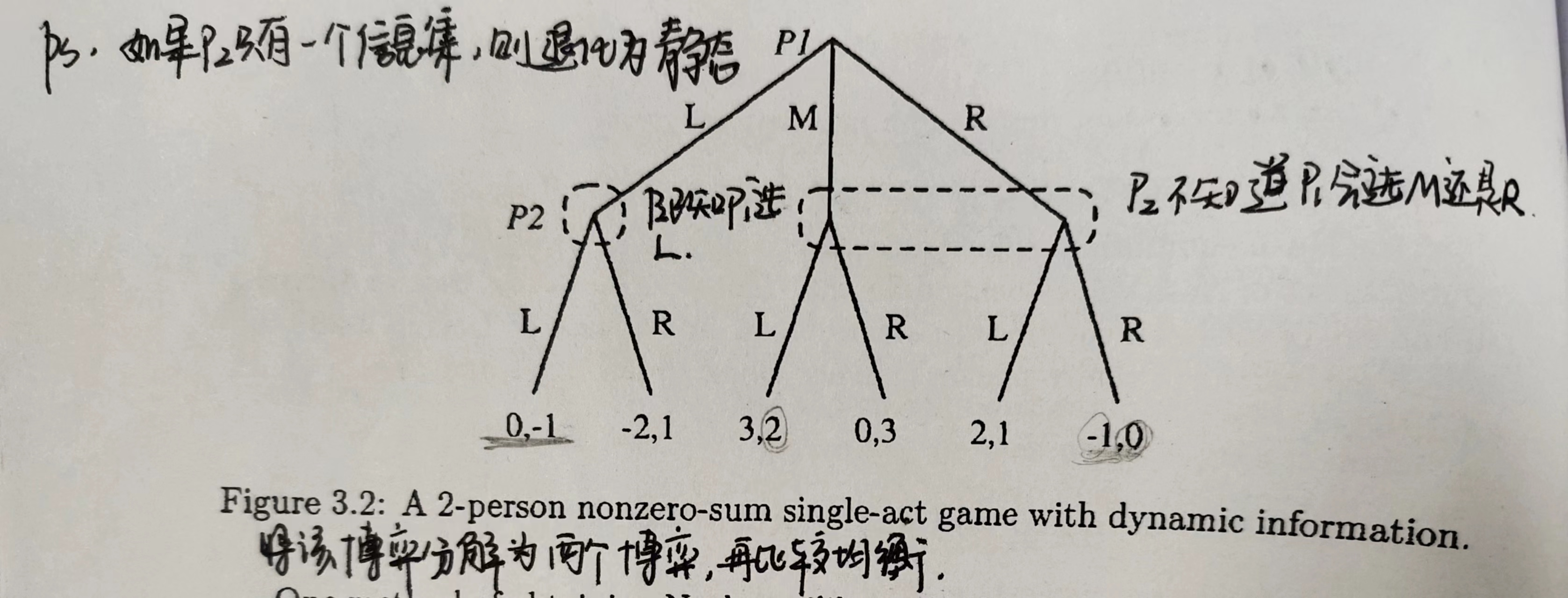
上图时二人单步博弈,P1先行动P2后行动,P1有3个可选择行动,P2有2个可选择行动。
重点关注一下信息集,在P2进行决策时候,如果P1选择行动L,那么P2在决策时是能够观察这个信息的;但如果P1选择行动M/R,这时候P2就不能确定是哪个,也就是这时候P2不知道P1选的是M/R,只知道P1没有选择L。
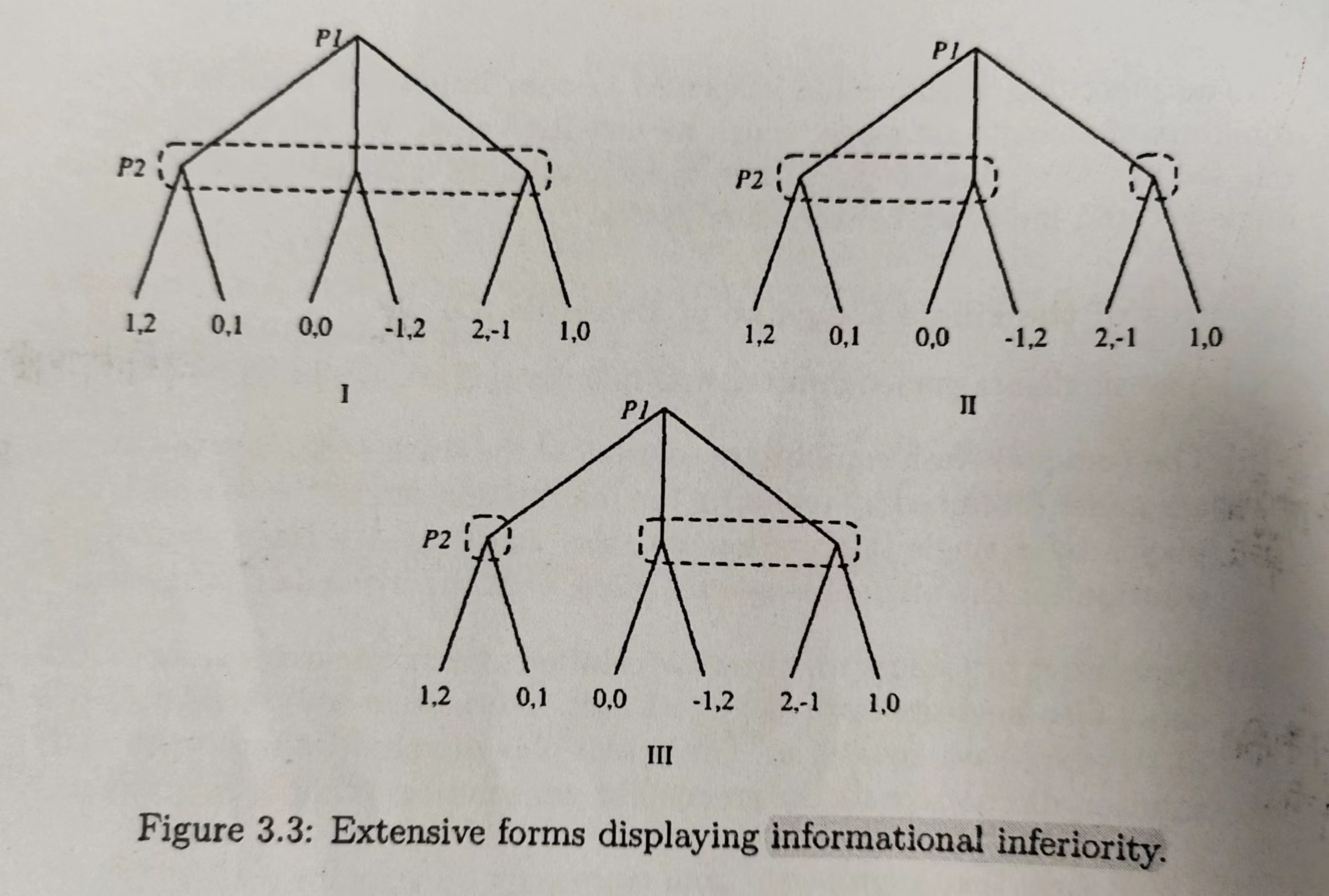
上图中三个差别就是在信息集的区别,显然,2和3与1相比,有着更多的信息。我们称博弈1信息低于2,3。而2,3之间并没有这种关系。
实际上,我们有博弈之间信息集“低于”的定义如下。
Definition 3.14 inferior
Definition 3.14 Let and be two single-act -person games in extensive form ,and further let and denote the strategy sets of in and ,respectively. Then , is said to be informationally inferior to if for all ,with strict inclusion for at least one .
两个博弈在均衡关系有以下定理。
Proposition 3.7 Let be an -person single-act game that informationally inferior to some other single-act -person game ,say . Then
- any Nash equilibrium solution of also constitues a Nash equilibrium solution for ,
- if is a Nash equilibrium solution of so that for all ,then it also constitues a Nash equilibrium solution for
ladder-nested
定义 Definition 3.15 nested/ladder-nested
Definition 3.15
In an extensive form of a single act nonzero-sum finite game with a fixed order of play, a player is said to be a precedent of another player if the former is situated closet to the vertex of the tree than the latter.
The extensive forrm is said to be nested if each player has access to thei nformation acquired by all his precedents.If, furthermore, the only diference(if any) between the information available to a player () and his closest (immediate) precedent (say ) involves only the actions of , and only at those nodes corresponding to the branches of the tree emanating from singleton information sets of , and this so for all players, the extensiuve form is said to be ladder-nested.
A single- act nonzero-sum finite gameis said to be nested(respectively, ladder-nested) if it admits an extensive form that is nested
(respectively, ladder-nested).17:Note that in 2-person single-act games the concepts of “nestednes" and "ladder-nstetes" coincide, and every extensive form is, by defnitin, ldder-nested
图示
Remark 3.7
The single act extensive forms of Figs. 3.1(a) and 3.2 are both ladder-nested.
If the extensive form of Fig. 3.1(a) is modified so that both nodes of P2 are included in the same information set, then it is only nested, but not ladder-nested, since P3 can differentiate between different actions of P1 but P2 cannot.
Finally, if the extensive form of Fig.3.1(a) is modified so that this time P3 has a single information set (see Fig. 3.4(a)), then the resulting extensive form becomes non-nested, since then even though P2 is a precedent of P3 he actually knows more than P3 does.
The single-act game that this extensive form describes is, however, nested since it also admits the extensive form description depicted in Fig. 3.4(b).
One advantage of dealing with ladder-nested extensive forms is that they can recursively be decomposed into simpler tree structures which are basically static in nature. This enables one to obtain a class of Nash equilibria of such games recursively, by solving static games at each step of the recursive procedure.
Before providing the details of this recursive procedure, let us introduce some terminology.
子集定义 Definition 3.16
Definition 3.16
For a given single- act dynamic game in nested extensive forrm (say, ), let denote a singleton information set of 's immediate follower (say ); consider the part of the tree structure of , which is cut off at , has as its vertex and has as immediate branches only those that enter into that inforrmation set of .
Then, this tree structure is called a sub-extensive form of. (Here, we adopt the convention that the starting vertex of the original extensive form is the singleton inforrmation set of the first-acting player. )
拆解1 将ladder-nested 拆解为静态的
Definition 3.17
A sub-extensive form of a nested extensive form of a single-act game is static if every player appearing in this tree structure has a single information set.
图示:
Remark 3.8 The single act game depicted in Fig3.2 admits two sub-extensive forms which are as follows:
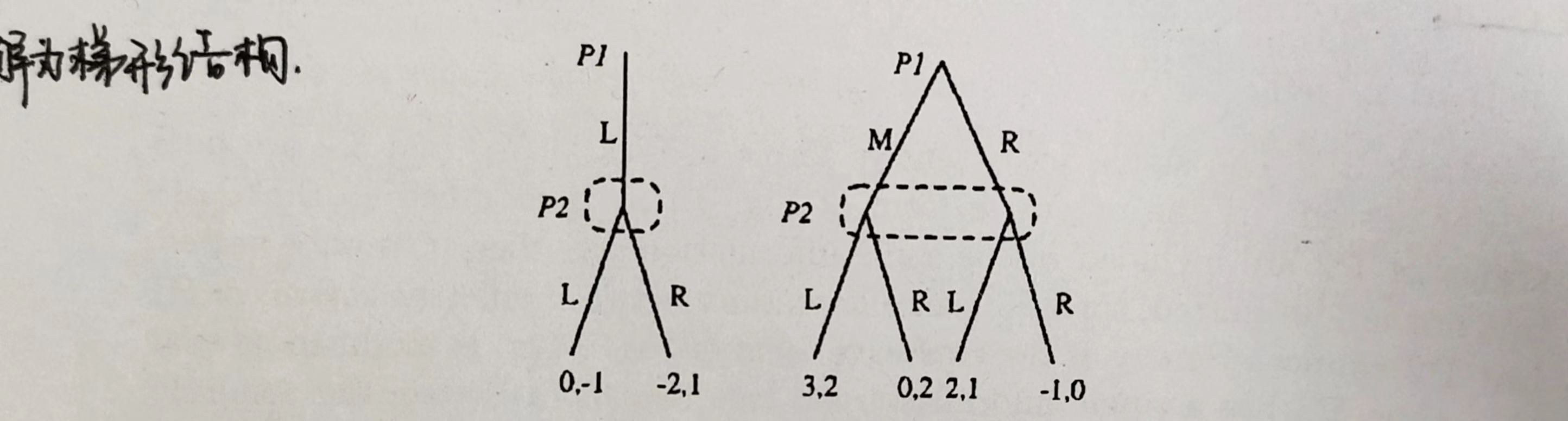
The extensive form of Fig. 3.1(a), on the other hand, admits a total of for sub-extensive forms which we do not display here. It should be noted that each sub-extensive form is itself an extensive form describing a simpler game. The first one displayed above describes a degenerate 2-player game in which P1 has only one alternative. The second one again describes a 2-player game in which the players each have two alternatives. Both of these sub-extensive forms will be called static since the first one is basically a one player game and the second one describes a static 2-player game.
也就是说可以对信息集进行分解,将梯形结构拆解为简单的静态博弈。
下面给出一个例子
拆解2 将nested拆解为动态的 Definition 3.19
Definition 3.19 A nested extensive (or sub-extensive) form of a single-act game is said to be undecomposable if it does not admit any simpler sub-extensive form. It is said to be dynamic, if at least one of the players has more than one information set.
图示:
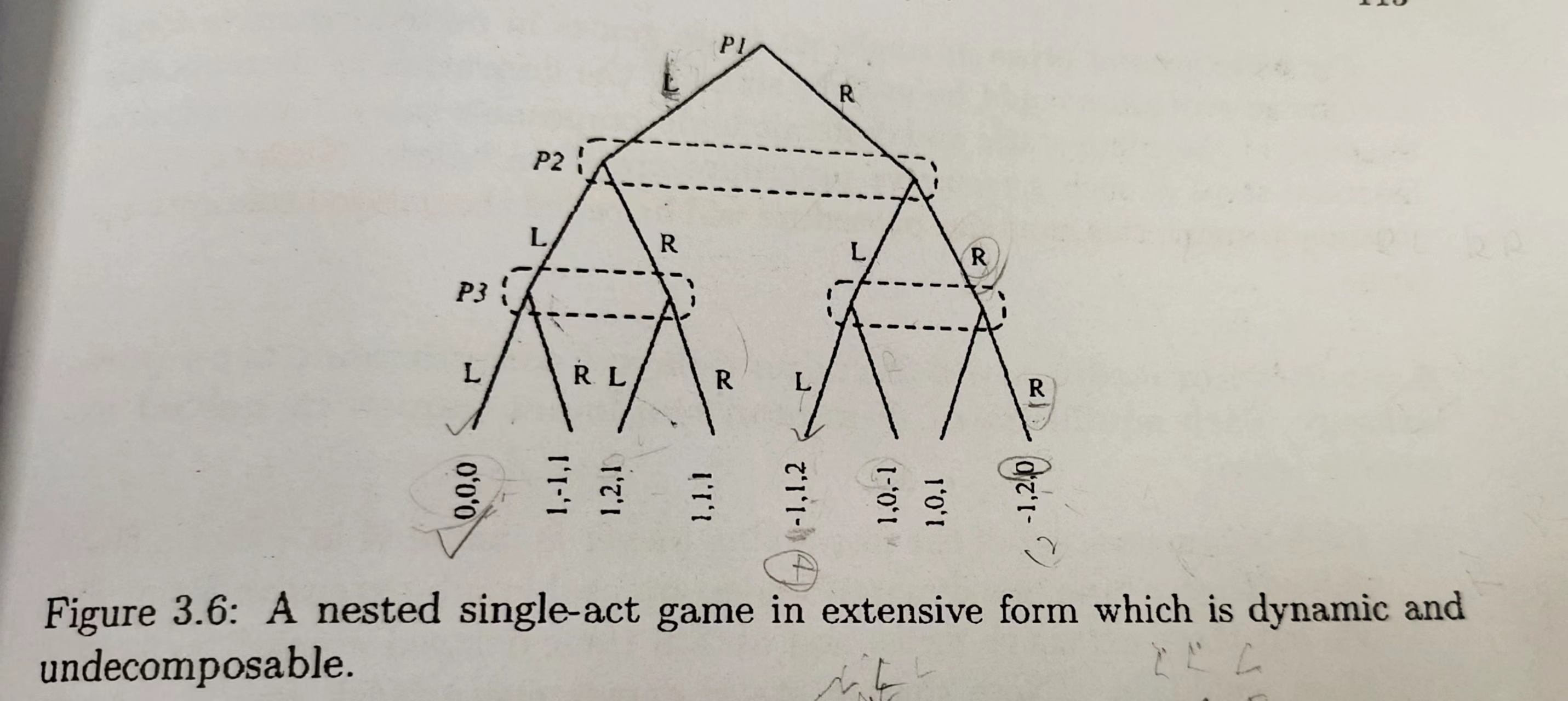
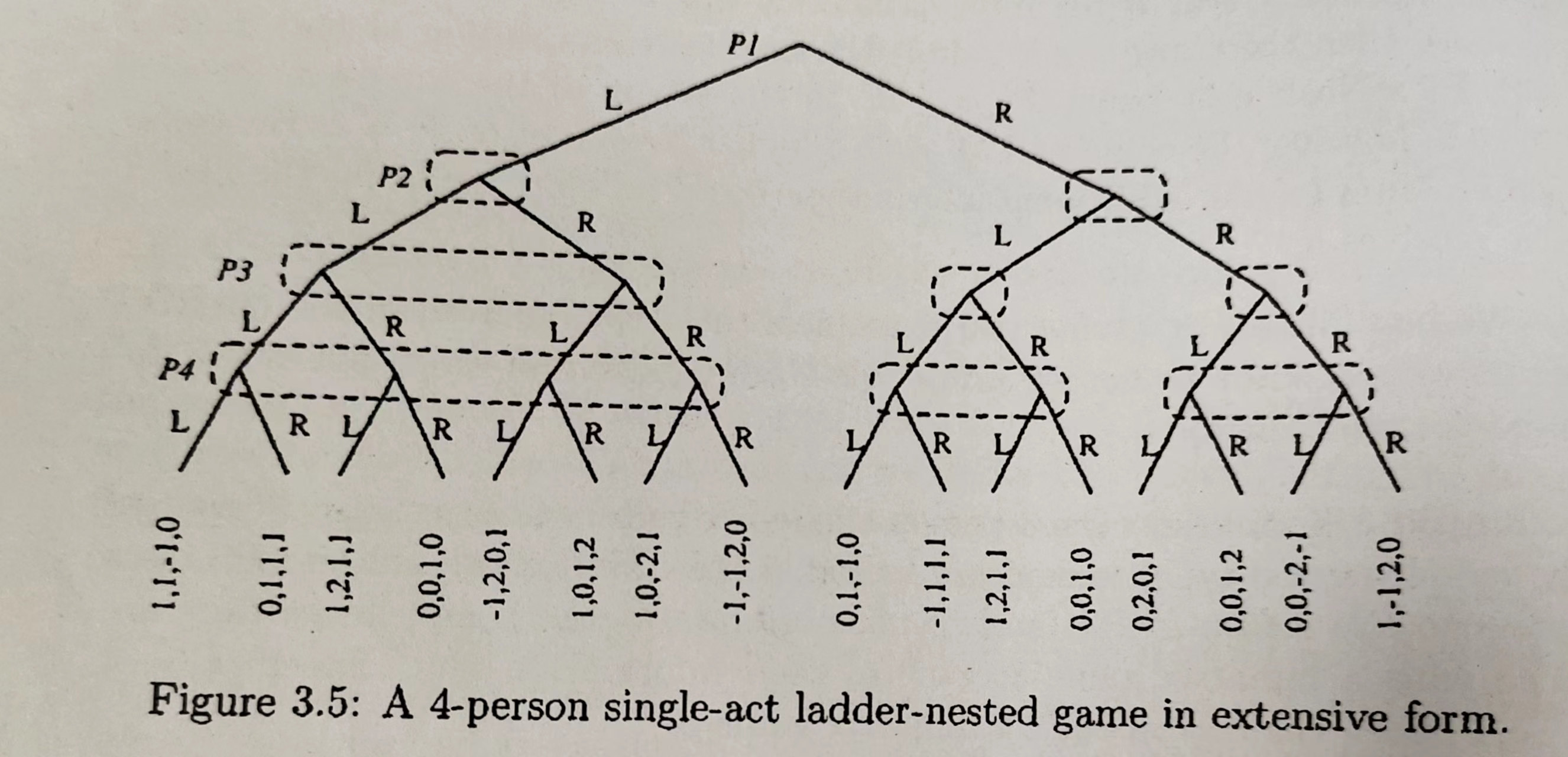
N人非零和feedback型的扩展型
定义 Definition 3.21
Definition 3.21 A muiti-act N -person nonzero-sum game in extensive form with a fixed onder of play is called an N-person
nonzero-sum feedback game Jin extensive form, if
at the time of his act, each player has perfect information concerning the current level of play, i.e.,no information set contains nodes of the tree belonging to different levels of play,
information sets of the first- acting player at every level of play are singletons, and the information sets of the other players at every level of play are such that none of them includes nodes corresponding to branches emanating from two or more different information sets of the first-acting player, i.e., each player knows the state of the game at every level of play.
If, furthermore,
the single-act games corresponding to the information sets of the first-acting player at each level of play are of the ladder-nested (respectively nested) type (cf. Def. 3.15), then the multi-act game is clled an N-person nonzer-sum fedack game in ladder nested (eseptivele, neste) extensive form.
Background
扩展型博弈 Extensive Form Games
an extensive form game is a tuple .
-
is a set of states, including , the initial state of the game. A state can alsobe called a history, because a game state is exactly history of the sequence of actions taken from the initial state. I will use to indicate concatenation,so is the sequence of actions in , followed by action .
:状态序列的集合
对于任何一个在集合中的序列,它是一个在某一次游戏中发生状态的序列,将此次博弈中发生的所有动作按照时间先后依次排列起来即得到。从博弈树的角度来讲,是从根节点到达博弈树中任意某个节点的路径。基于此我们可以做如下定义: 表示是的子串, 表示是的真子串。对应到博弈树中则表示是的一个孩子节点。
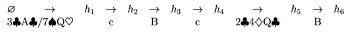
图1表示的是德州扑克中的一个包含动作和状态的序列,箭头下方的字符表示每个玩家做出的动作,小写字母表示玩家1的动作,大写字母表示玩家2的动作,描述牌型的字符串是机会玩家的动作(可理解为发牌员做出的动作)。字母c是call动作的缩写,字母b是bet动作的缩写。
在图1中,状态h5为状态h6的子串,状态h6是状态h5在博弈树中的孩子节点;状态h1为状态h2、h3、h4、h5、h6的子串,状态h2、h3、h4、h5、h6都是状态h1在博弈树中的孩子节点。
-
is the set of terminal (leaf) states, and gives the payoff to player p if the game ends at state .
: 终止状态的集合(对应博弈树中的叶子节点)
:一个由终止状态到实数的映射,表示某个玩家到达终止状态时可以获得的奖励
-
is a set of all players acting in the game,
:参与游戏的所有玩家的集合
and is a function which describes which player is currently acting at a non-terminal state .
:一个非终止状态到中某一玩家的映射,表示当前状态应该由哪位玩家采取行动
The actions available at a non-terminal state are defined implicitly by the set of histories , so that .
注意这个 $ h\cdot aha$
For a history where a stochastic event is about to happen, like a die roll or card deal, is a special“ chance player” . The value gives the probability of chance event occurring if the game is in state .
:机会玩家(可理解为发牌员)做出所有合法动作的概率分布,可进一步用 来表示当游戏处于状态时,机会事件发生的概率
-
describes what information is hidden from the players in a game, defined by a partition of all non-terminal, non-chance states.
must satisfy the constraints that and , we have and .
A set is called an information set, and for every state the player will only know that the current state of the game is one of the states in, but not exactly which one.
:玩家的信息集,一个信息集中包含了若干个中的状态,当其他玩家通过观测历史时,只知道玩家处于集合上,但是并不清楚该玩家具体在的哪一个状态上。可以利用信息集的大小来衡量一个玩家在游戏中隐藏了多少信息
玩家策略
策略的描述
A player’s strategy, also known as their policy, determines how they choose actions at states where they are acting .The term strategy profile is used to refer to a tuple consisting of a strategy for each player.
策略是玩家在游戏中选择动作的准则,在非完备信息博弈中,策略是一个从当前信息集上所有合法动作到之间的一个映射,也可以说是一个基于信息集的动作的概率分布
I will use to refer to a strategy for player , and to refer to a strategy profile .
Given a strategy profile and some player strategy , I will use the tuple to refer to the strategy profile where player ’s strategy is , and their opponent plays according to their strategy in .
策略的概率 Strategy Probabilities
gives the probability of player making action given they have reached information set$ I \in \mathcal{I}{p} \sigma(I, a)=\sigma(I, a) $. I will use the vector to speak of the probability distribution over .
$ \sigma_{p}(I, a) pIa$的概率
:表示一个概率分布,即处于状态集时,做出所有合法动作的概率分布(将游戏中所有的信息集上的 组合起来,即可得到完整的策略
gives the probability of reaching state if all players follow profile .
gives the probability of reaching state if chance and ’s opponents make the actions to reach , and player acts according to .
We can also extend the notation by flipping which players are following and use to refer to the probability of reaching state if player makes the actions to reach , and chance and ’s opponents act according to .
All of these probabilities can also be extended to consider subsequences of actions. We can speak of as the probability of player making the actions needed to move from state to state .
:从初始状态出发,当所有玩家都遵循策略时,到达状态的概率
:玩家从初始状态出发,遵循策略,到达状态的概率
:从初始状态出发,除玩家外,其他所有玩家都遵循策略,到达状态的概率。
:玩家遵循策略,从状态出发,到达中止状态的概率
关于概率这一定义,有以下三个等式需要额外注意:
1. $ \pi{\sigma}(h)=\pi_{p}(h) \pi_{-p}^{\sigma}(h) $ :这个等式表明所有玩家遵循策略到达状态的概率等于每个玩家分别遵守策略到达状态的概率相乘;
这个式子是关于玩家的方向来看,多人游戏,想要到达某个状态不但取决于玩家的策略
2. $ \pi_{p}^{\sigma}(I, a)=\pi_{p}^{\sigma}(I) \sigma(I, a) πσ(I^k,a) $概率的乘积;
其中右边代表玩家从初始状态出发,遵循策略,到达到达信息集的概率 ,表示在信息集下做出动作的概率
左边的就表示代表玩家从初始状态出发,遵循策略,到达到达信息集,并做出动作的概率
3. $ \pi{\sigma}(z)=\pi(h) \pi^{\sigma}(z \mid h) $ :这个等式是等式2的推论,表明从初始状态出发,遵循策略到达状态的概率等于从初始状态出发,遵循策略到达状态(h是z的子串)的概率乘以遵循策略,从状态出发到达状态的概率。
这个式子是从路径的长度来看的,总路径和中间结点的关系
本文来自博客园,作者:{珇逖},转载请注明原文链接:https://www.cnblogs.com/zuti666/p/16909238.html







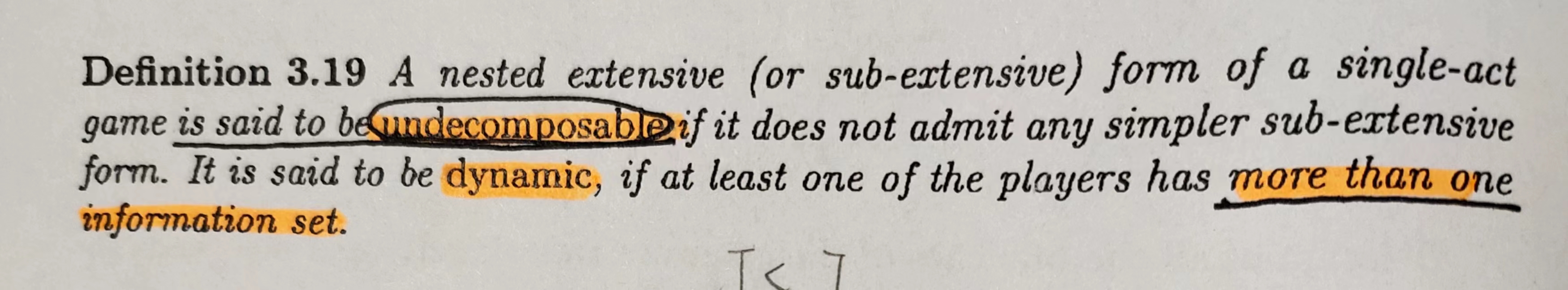



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律
2021-11-20 知识扩展4——拉格朗日乘数,KKT条件,对偶问题
2021-11-20 支持向量机 SVM