博弈论与强化学习 算法 一 MinimaxQ, NashQ ,FFQ
博弈解与强化学习
二 基础算法
2.1 引言
一个随机博弈可以看成是一个多智能体强化学习过程,但其实这两个概念不能完全等价,随机博弈中假定每个状态的奖励矩阵是已知的,不需要学习。而多智能体强化学习则是通过与环境的不断交互来学习每个状态的奖励值函数,再通过这些奖励值函数来学习得到最优纳什策略。通常情况下,模型的转移概率以及奖励函数为止,因此需要利用到Q-learning中的方法来不断逼近状态值函数或动作-状态值函数。
在多智能体强化学习算法中,两个主要的技术指标为合理性与收敛性。
合理性(rationality)是指在对手使用一个恒定策略的情况下,当前智能体能够学习并收敛到一个相对于对手策略的最优策略。
收敛性(convergence)是指在其他智能体也使用学习算法时,当前智能体能够学习并收敛到一个稳定的策略。通常情况下,收敛性针对系统中的所有的智能体使用相同的学习算法。
针对应用来分,多智能体强化学习算法可分为零和博弈算法与一般和博弈算法。
本文主要介绍四种多智能体强化学习算法,主要介绍每种算法的应用特性与应用公式,具体的收敛性证明后面每个算法单开一章讲。
2.2 Minimax-Q算法
相关论文
Littman, Michael L. "Markov games as a framework for multi-agent reinforcement learning." Machine learning proceedings 1994. Morgan Kaufmann, 1994. 157-163.
cited: 2970
Machine Learning Proceedings 1994 : Proceedings of the Eleventh International Conference, Rutgers University, New Brunswick, NJ, July 10–13, 1994
Michael Littman Michael Littman - Google Scholar
[本地](./Markov games as a framework for multi-agent reinforcement learning.pdf)
相关论文
Kaelbling, Leslie Pack, Michael L. Littman, and Andrew W. Moore. "Reinforcement learning: A survey." Journal of artificial intelligence research 4 (1996): 237-285.
cited: 9518
Journal of Artificial Intelligence Research (JAIR) dblp: Journal of Artificial Intelligence Research (JAIR) (uni-trier.de)
Leslie Kaelbling
Leslie Kaelbling - Google Scholar
https://www.youtube.com/watch?v=Er7Dy8rvqOc
[本地](./Reinforcement learning A survey.pdf)
简述
Minimax-Q算法应用于两个玩家的零和随机博弈中。
Minimax-Q中的Minimax指的是使用minimax方法构建线性规划来求解每个特定状态s的阶段博弈的纳什均衡策略。Q指的是借用Q-learning中的TD方法来迭代学习状态值函数或动作-状态值函数。
在两玩家零和随机博弈中,给定一个状态,则定义第个智能体的状态值函数为
表示智能体 的对手。$ Q_{i}^{}\left(s, a_{i}, a_{-i}\right) Q_{i}^{}(\cdot) s Q_{i}^{*}(\cdot) Q_{i}\left(s, a_{i}, a_{-1}\right) $ 值。
算法流程
整个算法流程如下

理想情况,如果算法能够对每一个状态-动作对访问无限次,那么该算法能够收敛到纳什均衡策略。但是在上述算法中存在几个缺点:
- 在第5步中需要不断求解一个线性规划,这将造成学习速度的降低,增加计算时间。
- 为了求解第5步,智能体 需要知道所有智能体的动作空间,这个在分布式系统中将无法满足。
- 只满足收敛性,不满足合理性。Minimax-Q算法能够找到多智能体强化学习的纳什均衡策略,但是假设对手使用的不是纳什均衡策略,而是一个较差的策略,则当前智能体并不能根据对手的策略学习到一个更优的策略。该算法无法让智能体根据对手的策略来调节优化自己的策略,而只能找到随机博弈的纳什均衡策略。这是由于Minimax-Q算法是一个对手独立算法(opponent-independent algorithm),不论对手策略是怎么样的,都收敛到该博弈的纳什均衡策略。就算对手采用一个非常弱的策略,当前智能体也不能学习到一个比纳什均衡策略更好的策略。
2.3 Nash Q-Learning算法
相关论文
Hu J, Wellman M P. Nash Q-learning for general-sum stochastic games[J]. Journal of machine learning research, 2003, 4(Nov): 1039-1069.
cited: 1188
Journal of machine learning research, 机器学习顶刊 JMLR ,但中科院3区
[本地](.\Nash Q-learning for General-Sum Games.pdf)
简述
Nash Q-Learning算法是将Minimax-Q算法从零和博弈扩展到多人一般和博弈的算法。在Minimax-Q算法中需要通过Minimax线性规划求解阶段博弈的纳什均衡点,拓展到Nash Q-Learning算法就是使用二次规划求解纳什均衡点。
Nash Q-Learning算法在合作性均衡或对抗性均衡的环境中能够收敛到纳什均衡点,其收敛性条件是,在每一个状态s的阶段博弈中,都能够找到一个全局最优点或者鞍点,只有满足这个条件,Nash Q-Learning算法才能够收敛。
与Minimax-Q算法相同,Nash Q-Learning算法求解二次规划的过程也非常耗时,降低了算法的学习速度。
论文精读
在强化学习中,每个智能体的目标是学习使得价值函数最大化的策略,而单个智能体的收益依赖于联合策略,因为联合策略是包含了所有参与者的策略,所以需要考虑到随机博弈的Nash equilibrium
下面给出在多智能体随机博弈下纳什均衡的定义,
其中代表联合Nash equilibrium策略,代表除参与者以外的所有参与者的联合策略。
在Nash Equilibrium中,每个智能体都会采取最优反应策略 the best response)
已有证明,在N人随即博弈中,至少有一个静止策略的纳什均衡,于是,给定Nash equilibrium策略 ,就能够计算出一个在Nash equilibrium策略下的价值函数值。
下表说明了在多智能体的情形下Q-function与单智能体下Q-function的不同
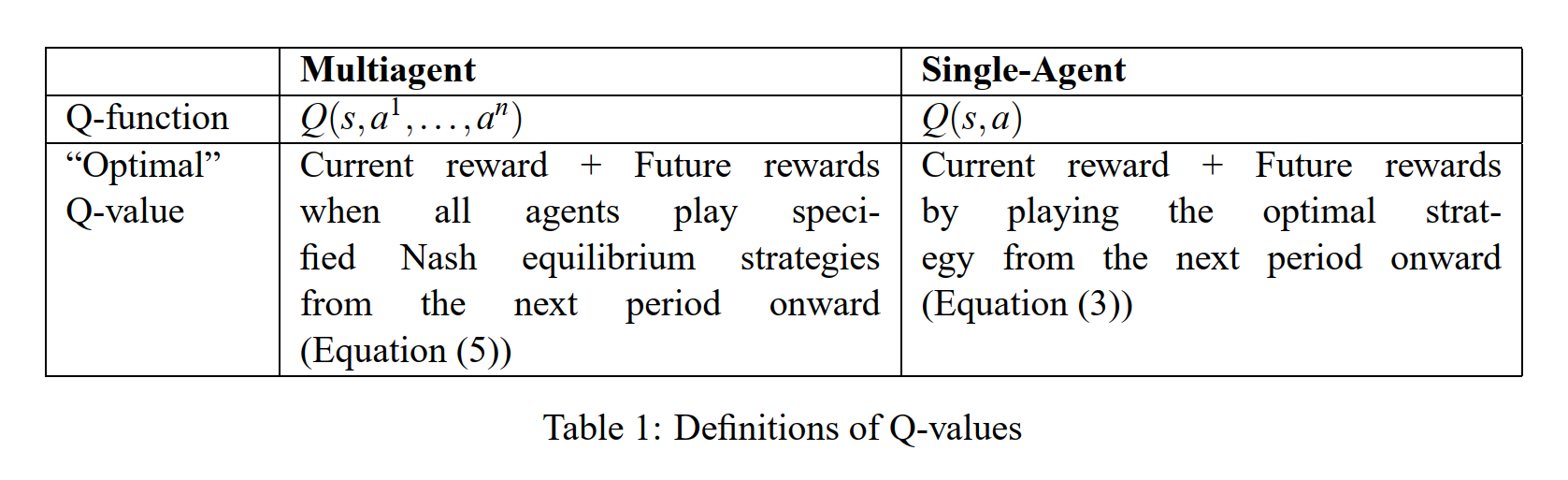
Nash Q-learning 把Q-larning从单智能体推广到多智能体的核心在于:
The Q-learning algorithm we propose resembles standard single-agent Q-learning in many ways, but differs on one crucial element: how to use the Q-values of the next state to update those of the current state. Our multi agent Q-learning algorithm updates with future Nash equilibrium payoffs,whereas single-agent Q-learning updates are based on the agent’s own maximum payoff. In order to learn these Nash equilibrium payoffs, the agent must observe not only its own reward, but those of others as well
Nash Q-learning 的更新过程:
Our learning agent, indexed by , learns about its Q-values by forming an arbitrary guess at time.One simple guess would be letting for all . At each time , agent observes the current state, and takes its action. After that, it observes its own reward, actions taken by all other agents, others’ rewards, and the new state . It then calculates a Nash equilibrium for the stage game , and updates its Q-values according to
where
Different methods for selecting among multiple Nash Equilibrium will in general yield different updates. is agent i’s payoff in state for the selected equilibrium. Note that $ π1(s')···πn(s')·
Q_t^i(s') $ is a scalar. This learning algorithm is summarized in Table 2.
In order to calculate the Nash equilibrium , agent would need to know
.Information about other agents’ Q-values is not given, so agent must learn about them too. Agent forms conjectures about those Q-functions at the beginning of play, for example, for all and all . As the game proceeds, agent observes other agents’ immediate rewards and previous actions. That information can then be used to update agent ’s conjectures on other agents’ Q-functions. Agent updates its beliefs about agent ’s Q-function, according to the same updating rule (6) it applies to its own
Note that for$ (s,a1,\cdots,an) \neq (s_t,a_t1,\cdots,a_tn)$. Therefore (8) does not update all the entries in the Q-functions. It updates only the entry corresponding to the current state and the actions chosen by the agents. Such updating is called asynchronous updating
收敛性证明
算法流程
其算法流程如下:

该算法需要观测其他所有智能体的动作 与奖励值
。并且与Minimax-Q算法一样,只满足收敛性,不满足合理性。只能收敛到纳什均衡策略,不能根据其他智能体的策略来优化调剂自身的策略。
2.4、Friend-or-Foe Q-Learning算法
相关论文
Littman, Michael L. "Friend-or-foe Q-learning in general-sum games." ICML. Vol. 1. 2001.
cited: 633
ICML :International Conference on Machine Learning (ICML) 机器学习顶会
Michael Littman Michael Littman - Google Scholar
[本地](./The Friend-or-Foe Q-learning (FFQ) algorithm.pdf)
简述
Friend-or-Foe Q-Learning(FFQ)算法也是从Minimax-Q算法拓展而来。
为了能够处理一般和博弈,FFQ算法对一个智能体,将其他所有智能体分为两组,一组为的帮助一起最大化其奖励回报,另一组为的对抗并降低的奖励回报,因此对每个智能体而言都有两组。
这样一个n智能体的一般和博弈就转化为了一个两智能体的零和博弈。其纳什均衡策略求解方法如下所示
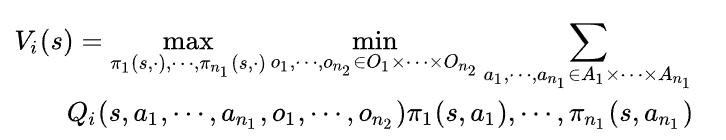
论文精读
收敛性证明
算法流程
算法流程如下:

有一种利用Minimax-Q算法进行多人博弈方法为,两队零和博弈,将所有智能体分成两个小组进行零和博弈。两队零和博弈中每一组有一个leader才控制这一队智能体的所有策略,获取的奖励值也是这一个小组的整体奖励值。
FFQ算法没有team learder,每个人选择自己动作学习自己的策略获得自己的奖励值,但是为了更新 值,每个智能体需要在每一步观测其他所有friend与foe的执行动作。
FFQ与Minimax-Q算法一样都需要利用线性规划,因此算法整体学习速度会变慢。
2.5、WoLF Policy Hill-Climbing算法
相关论文
Bowling, Michael, and Manuela Veloso. "Multiagent learning using a variable learning rate." Artificial Intelligence 136.2 (2002): 215-250.
cited: 962
Artificial Intelligence AIJ 人工智能顶刊
Michael Bowling
Michael Bowling - Google Scholar
Michael Bowling's Webpage (ualberta.ca)
[本地](./Multiagent learning using a variable learning rate.pdf)
简述
上述的三种方法都需要在学习过程中维护Q函数,假设动作空间 与状态空间 都是离散,假设每个智能体的动作空间相同,则对于每一个智能体都需要有一个 大小的空间来存储Q值,因此上述三种方法所需空间非常大。
为了解决上述问题,我们期望每个智能体只用知道自己的动作来维护Q值函数,这样空间就降到了 。WoLF-PHC就是这样的算法,每个智能体只用保存自己的动作来完成学习任务。WoLF-PHC是将“Win or Learn Fast”规则与 policy hill-climbing算法结合。
WolF是指,当智能体做的比期望值好的时候小心缓慢的调整参数,当智能体做的比期望值差的时候,加快步伐调整参数。
PHC是一种单智能体在稳定环境下的一种学习算法。该算法的核心就是通常强化学习的思想,增大能够得到最大累积期望的动作的选取概率。该算法具有合理性,能够收敛到最优策略。
论文精读
收敛性证明
算法流程
其算法流程如下

为了将PHC应用于动态环境中,将WoLF与PHC算法结合,使得智能体获得的奖励在比预期差时,能够快速调整适应其他智能体策略变化,当比预期好时谨慎学习,给其他智能体适应策略变化的时间。并且WoLF-PHC算法能够收敛到纳什均衡策略,并且具备合理性,当其他智能体采用某个固定策略使,其也能收敛到一个目前状况下的最优策略而不是收敛到一个可能效果不好的纳什均衡策略处。在WoLF-PHC算法中,使用一个可变的学习速率 来实现WoLF效果,当策略效果较差时使用 ,策略效果较好时使用 ,并且满足 。还有一个优势是,WoLF-PHC算法不用观测其他智能体的策略、动作及奖励值,需要更少的空间去记录Q值,并且WoLF-PHC算法是通过PHC算法进行学习改进策略的,所以不需要使用线性规划或者二次规划求解纳什均衡,算法速度得到了提高。虽然WoLF-PHC算法在实际应用中取得了非常好的效果,并且能够收敛到最优策略。但是其收敛性在理论上一直没有得到证明。其算法流程如下所示:

本文来自博客园,作者:{珇逖},转载请注明原文链接:https://www.cnblogs.com/zuti666/p/16909220.html




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律
2021-11-20 知识扩展4——拉格朗日乘数,KKT条件,对偶问题
2021-11-20 支持向量机 SVM