概率论3 随机变量及其分布

概率论3 随机变量及其分布

目录

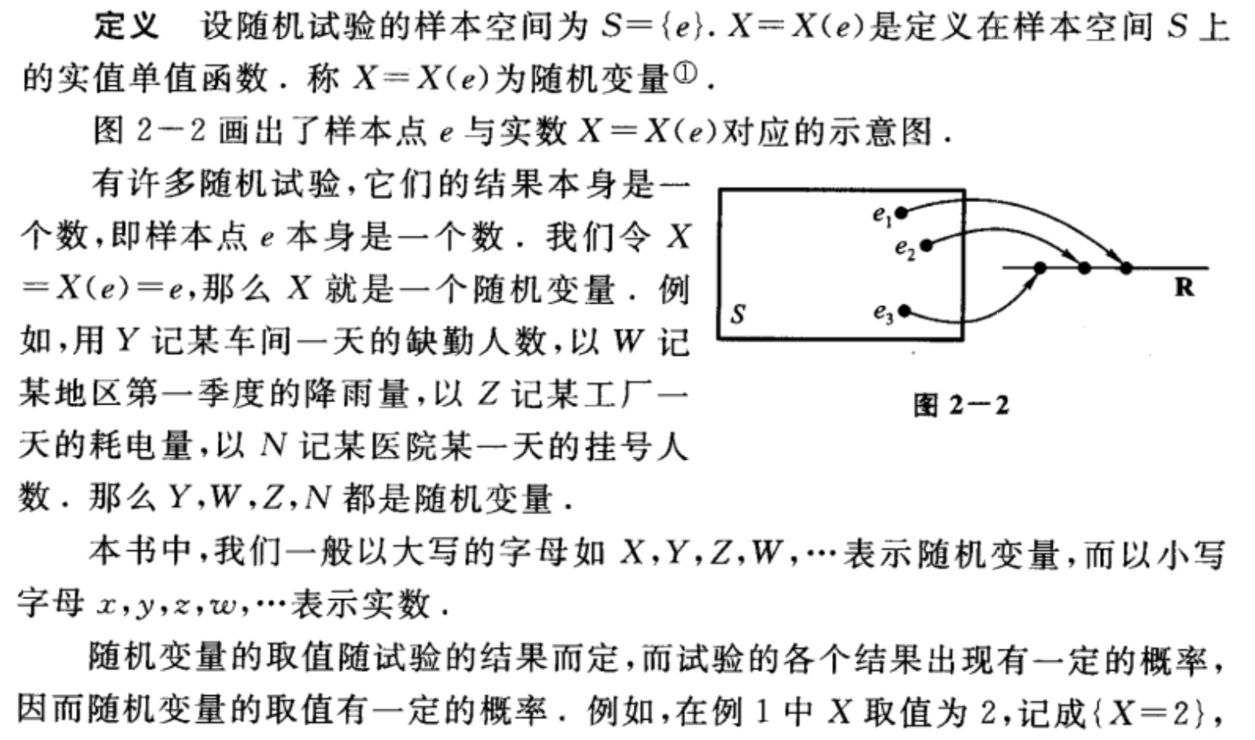
随机变量

image-20220316213553624

image-20220316213723403

离散型随机变量及其分布律

有些随机变量,它全部可能取到的值是有限个或可列无限多个,这种随机变量称为离散型随机变量。要掌握一个离散型随机变量X的统计规律,必须且只需知道X的所有可能取值以及取每一个可能值的概率。

image-20220316214034375

常见的离散型随机变量的分布律

一 （0-1）分布

image-20220316214232153

二 伯努利分布、二项分布

n次伯努利试验中事件\(A\)发生的次数

image-20220316214340253

image-20220316214352260

image-20220316214727437

image-20220316214750324

三 泊松分布

随机过程，第一个出现的时间

image-20220316215108895

分布函数

定义

image-20220318093857909

性质

image-20220318093922272

离散型随机变量的分布函数

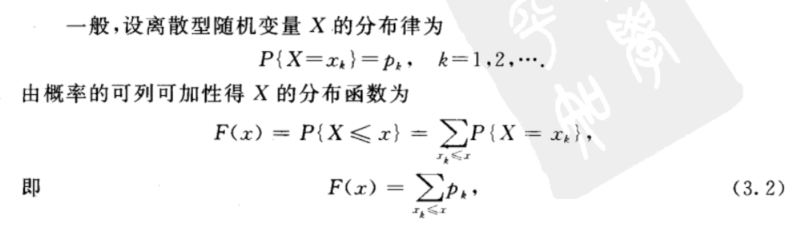
image-20220318093612743

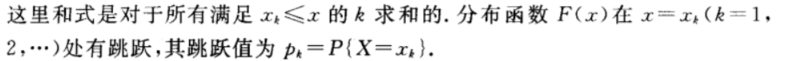
image-20220318093629527

连续型随机变量及其概率密度

定义

image-20220318094107036

性质

image-20220318094233507

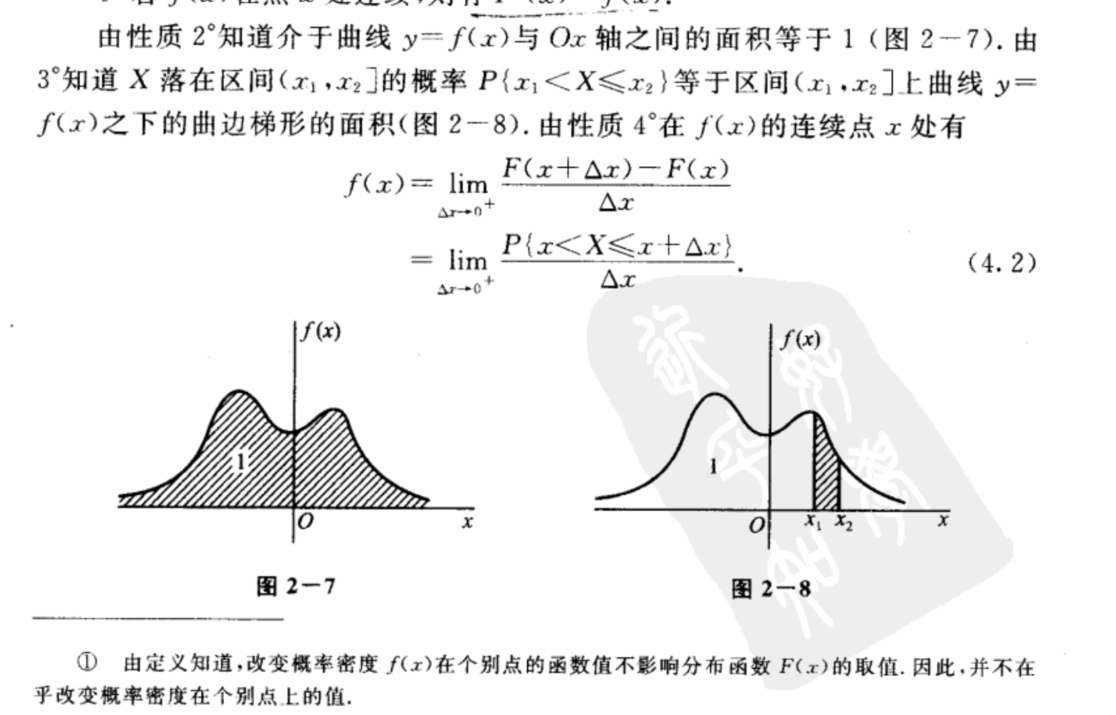
image-20220318094354437

image-20220318094442309

image-20220318094535309

常见的连续型随机变量的概率密度

一 均匀分布 \(X \sim U(a,b)\)

image-20220318094808945

image-20220318094848100

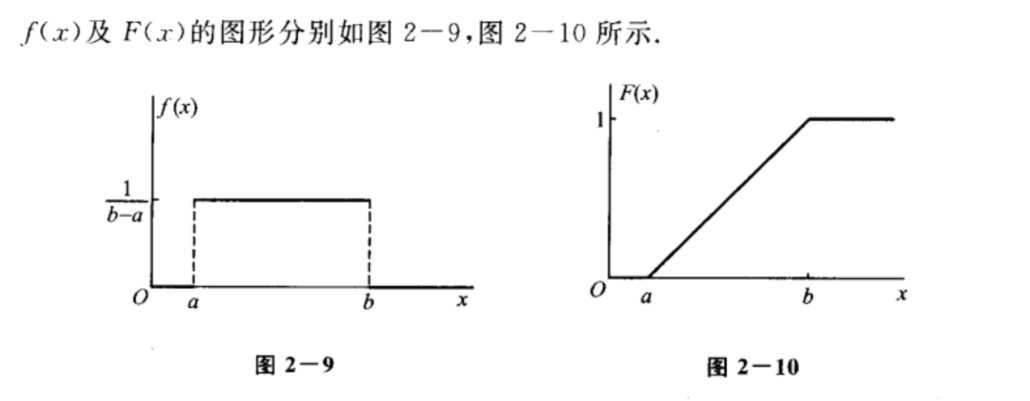
image-20220318094902222

二 指数分布

image-20220318095238332

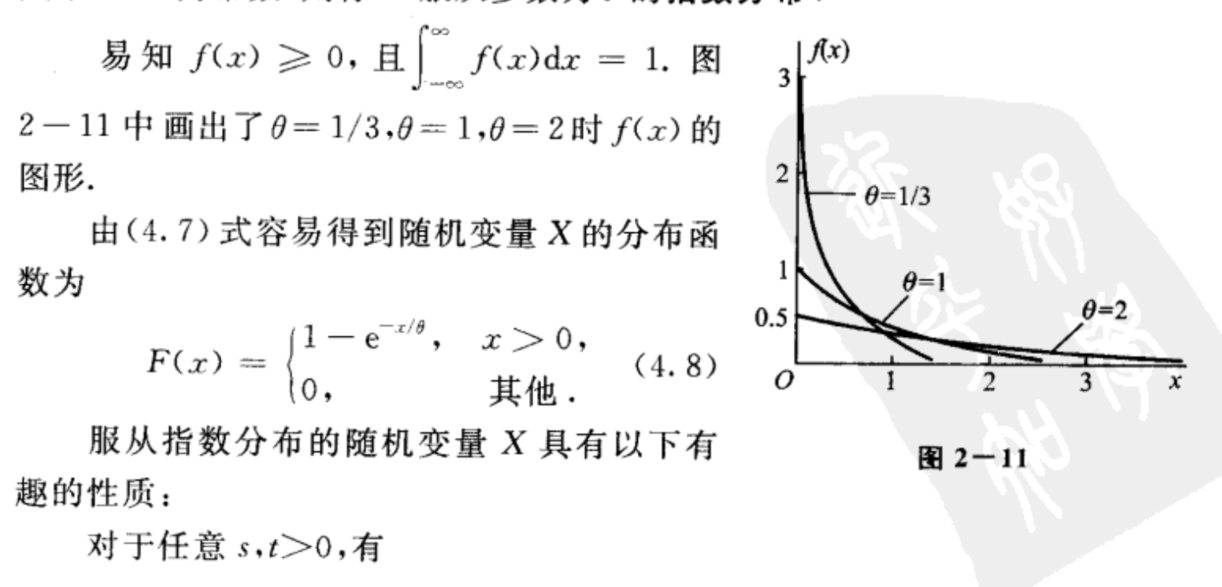
image-20220318095313989

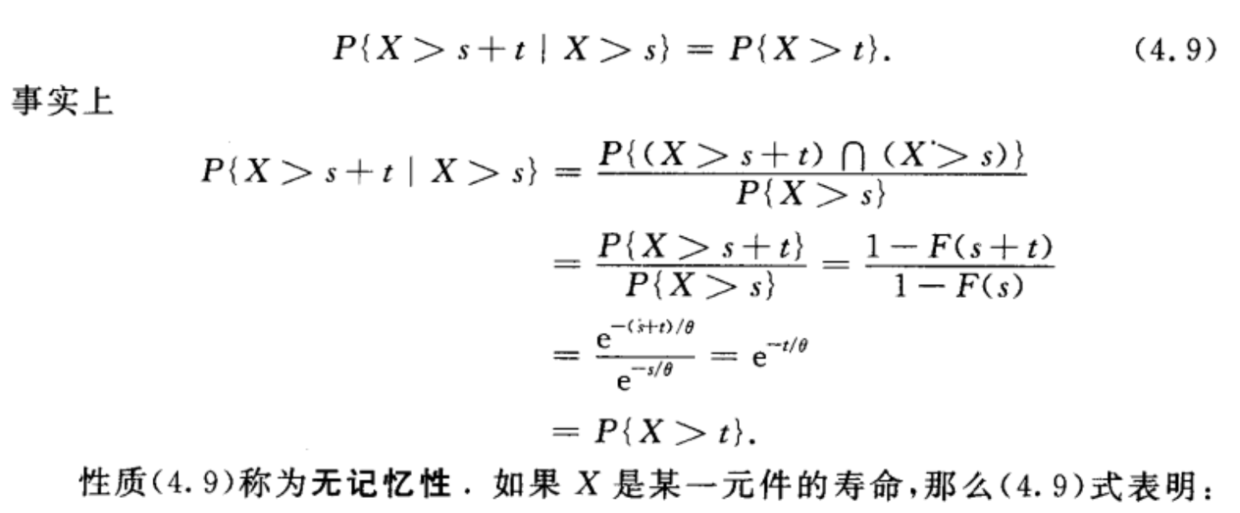
image-20220318095325788

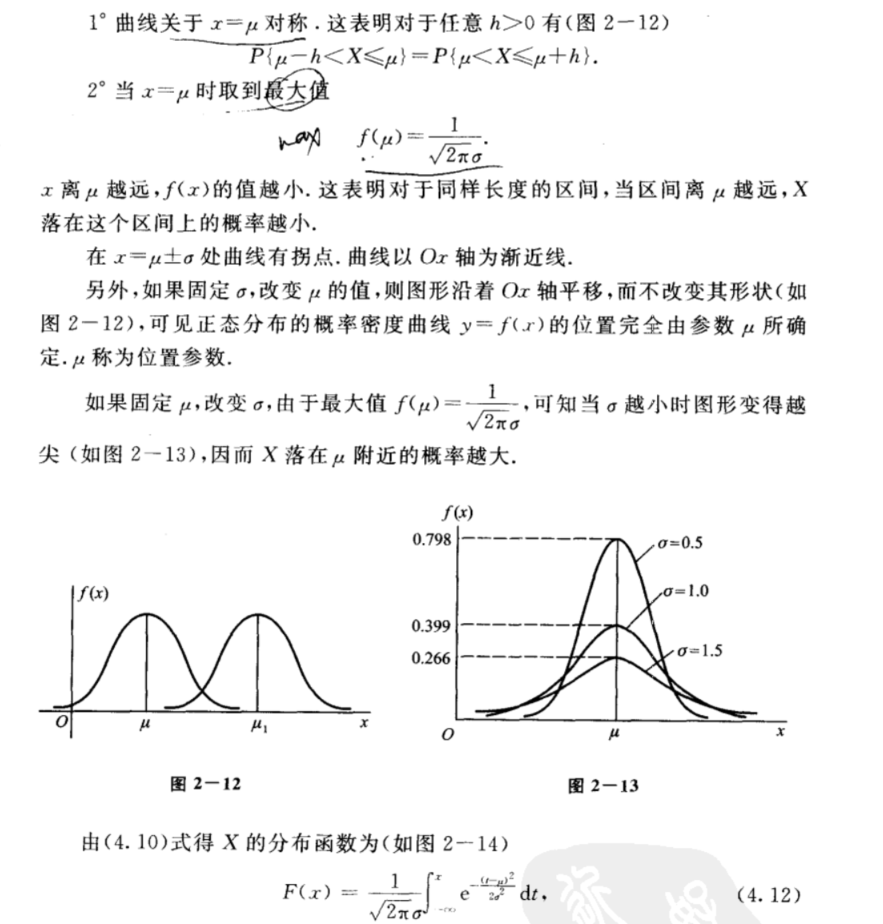
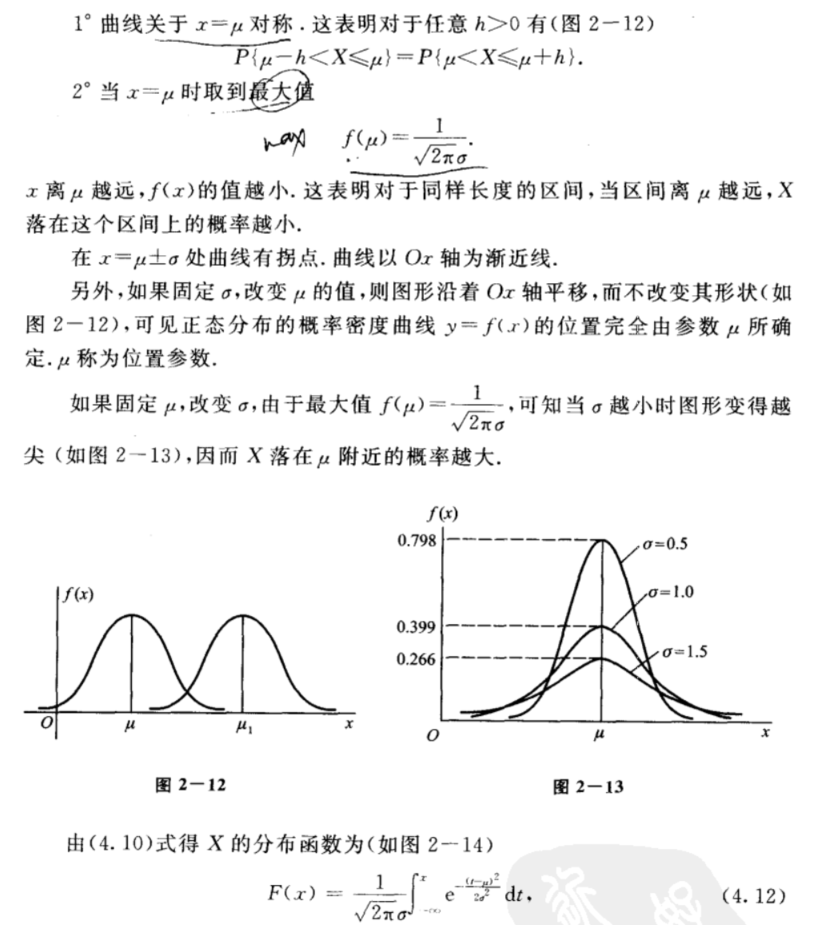
三 正态分布 （高斯分布）\(X \sim N(\mu,\delta^2)\)

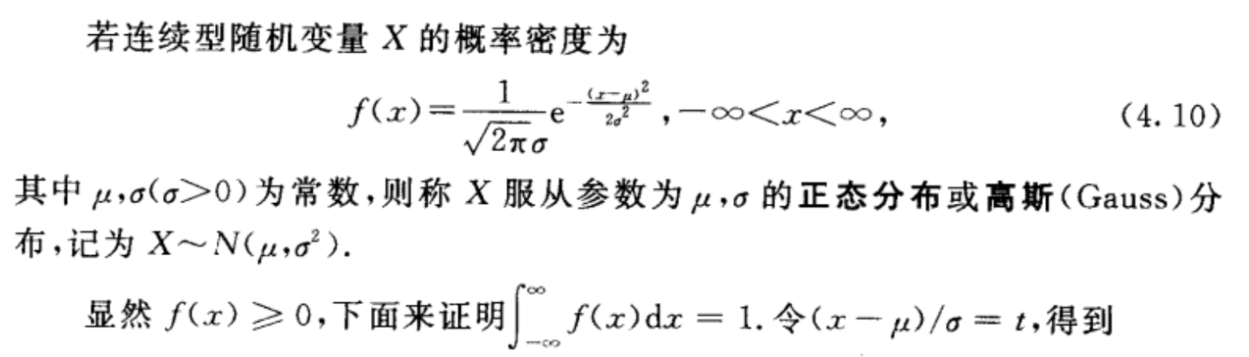
image-20220318095446349

正态分布函数的性质

image-20220318095806444

四 标准正态分布

image-20220318095606156

image-20220318100951094

正态分布转化为标准正态分布

image-20220318095709963

正态分布的线性组合也服从正态分布

image-20220318101426349

随机变量的函数分布

image-20220318101126525

image-20220318101222797

image-20220318101238602

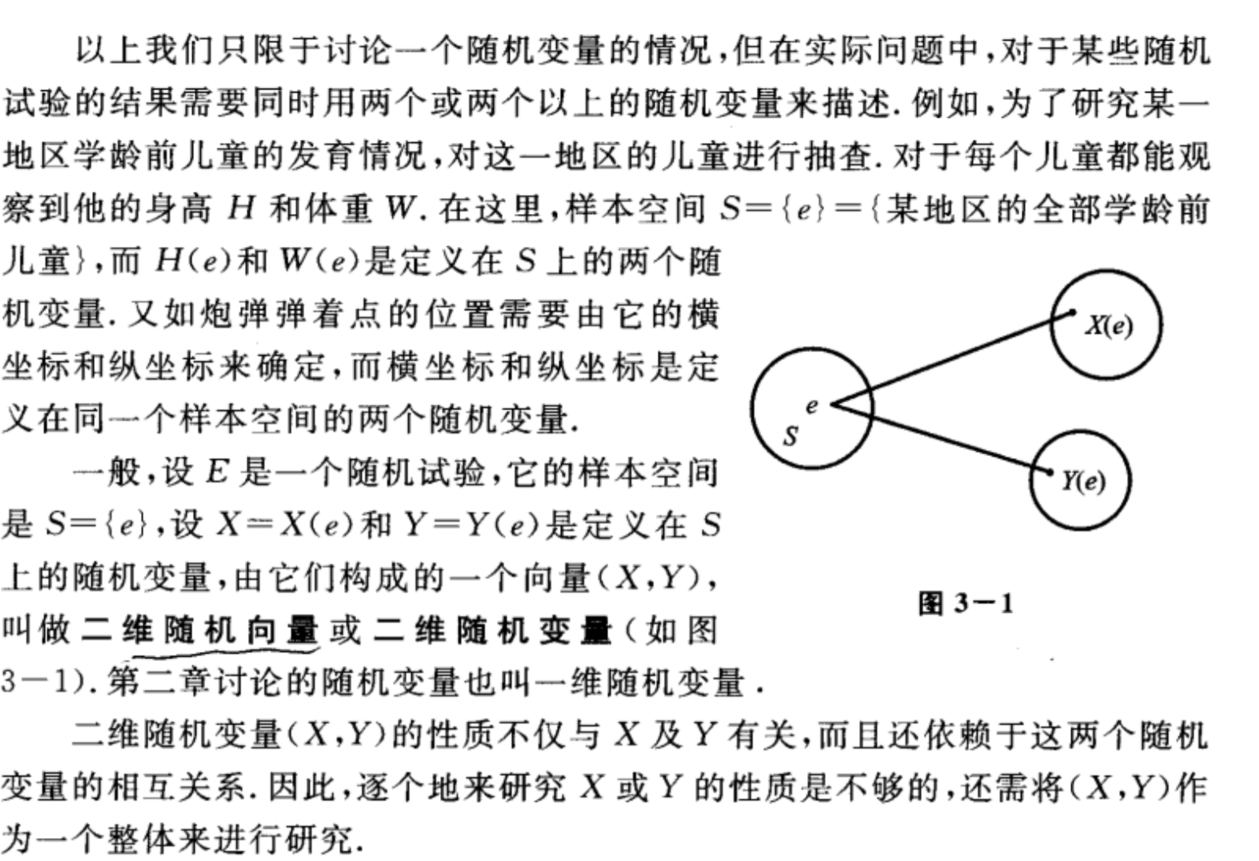
二维随机变量

二维随机变量的定义

image-20220318101534399

二维随机变量的分布函数

image-20220318101717955

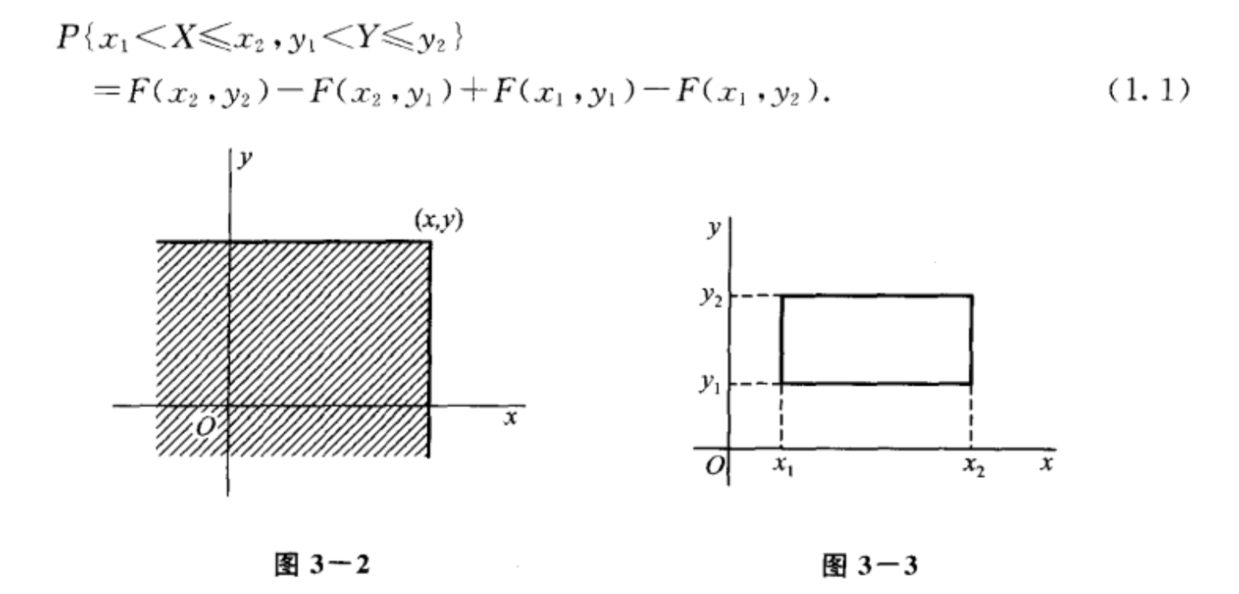
image-20220318101737532

分布函数的性质

image-20220318101827471

二维离散型随机变量的分布律

image-20220318102144979

image-20220318102156193

image-20220318102227800

连续型的二维随机变量的联合概率密度

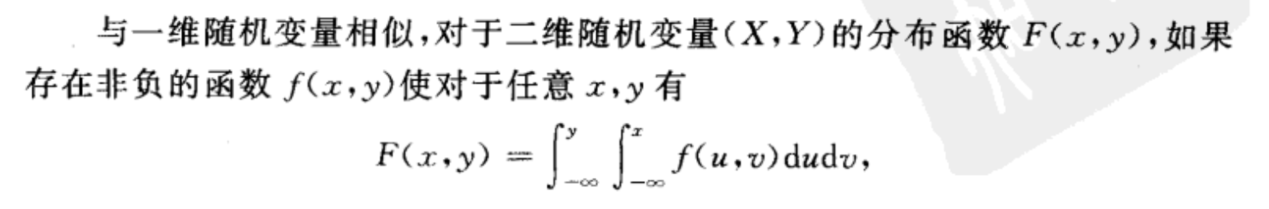
image-20220318102329623

image-20220318102349287

概率密度的性质

image-20220318102425347

n维随机变量

image-20220318102822169

边缘分布

边缘分布函数

image-20220318102942903

边缘分布律

image-20220318103000264

image-20220318103019415

边缘概率密度

image-20220318103033532

条件分布

条件分布律

image-20220318103253423

image-20220318103305657

image-20220318103212745

条件概率密度

image-20220318103424578

image-20220318103442783

image-20220318103459520

相互独立的随机变量

image-20220318111301278

image-20220318111312271

image-20220318111400186

两个随机变量的函数的分布

一 \(Z=X+Y\)

image-20220318111444727

相互独立的正态随机变量的线性组合仍然服从正态分布

image-20220318111522102

\(\Gamma\)的可加性

image-20220318111715408er

二 \(Z=\frac{Y}{X},Z=XY\)的分布

image-20220318112115958

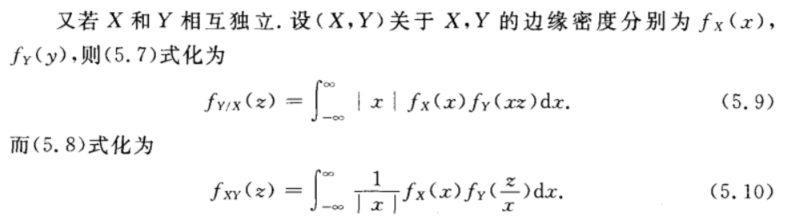
image-20220318112127220

三 \(M=max\{X,Y\},M=min\{X,Y\}\)的分布

image-20220318112231727

posted @ 2022-04-03 13:16  英飞  阅读(608)  评论(0)    收藏  举报