概率论1 随机试验与独立性

概率论1 随机试验与独立性

1 随机试验

随机试验

1. 可以再相同条件下重复进行
2. 每次试验的可能结果不止一个，并且能事先明确试验的所有可能结果；
3. 进行一次试验之前不能确定那一个结果会出现

2样本空间

（一）样本空间

对于随机试验，尽管在每次试验之前不能预知试验的结果，但饰演的所有可能结果组成的集合是已知的。

• 我们将随机试验\(E\)的所有可能结果组成的结果称为\(E\)​​的样本空间，记作\(S\).

• 样本空间的元素，即\(E\)​​的每个结果，称为样本点。

（二）随机事件

• 一般，我们称试验\(S\)的子集为\(E\)​​​​的随机事件，简称事件。在每次试验中，当且仅当这一子集的一个样本点出现时，称这一事件发生。

• 特别，由一个样本点组成的单点集，称之为基本事件。

• 样本空间\(S\)包含所有的样本点，它是\(S\)自身的子集，在每次试验中它总是发生的，\(S\)​​​称为必然事件。

• 空集\(\varnothing\)​不包含任何样本点，它也作为样本空间的子集，它在每次试验中都不发生，\(\varnothing\)称为不可能事件。

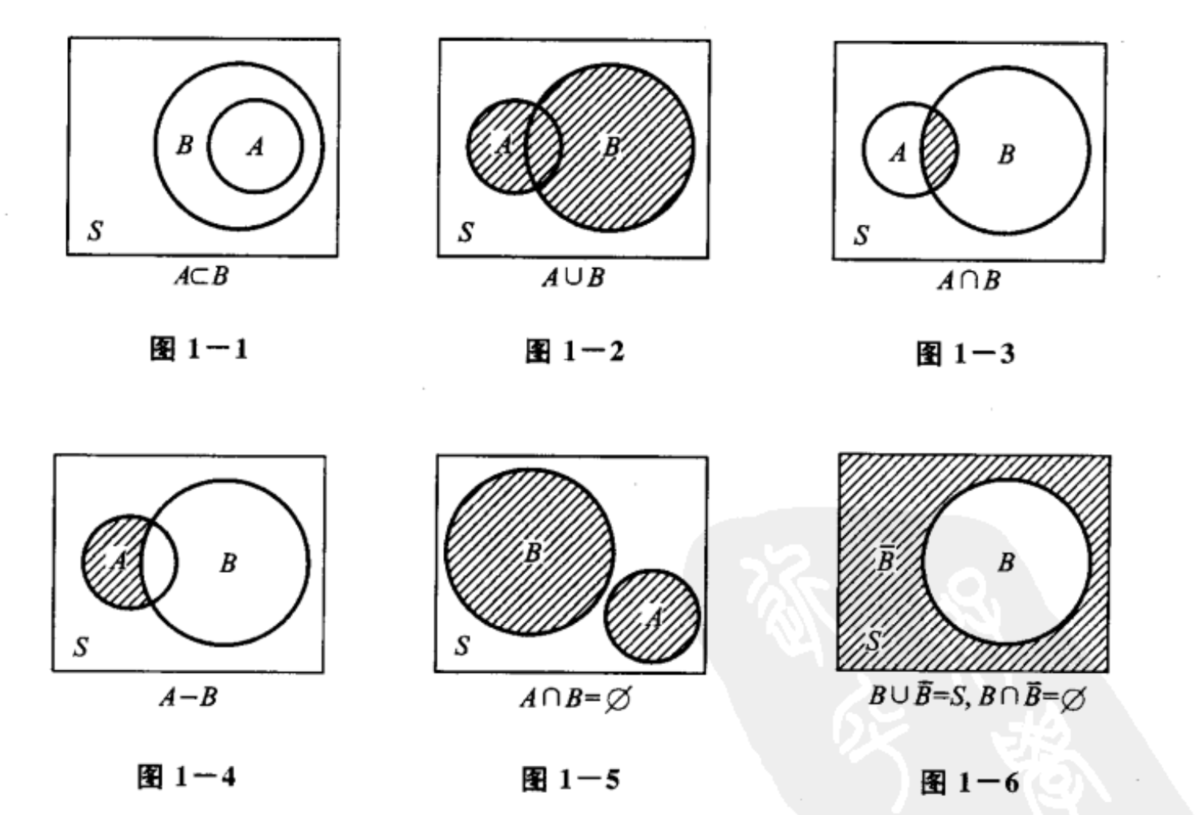
（三）事件间的关系与事件的运算

6 独立性

设\(A,B\)是试验E的两事件，若\(P(A)>0\),可以定义条件概率\(P(B|A)\).

一般,\(A\)的发生对\(B\)发生的概率是有影响的，这时\(P(B|A)≠P(B)\),

只有在这种影响不存在时才会有\(P(B|A)= P(B)\), 这时有\(P(AB)=P(B|A)P(A)=P(A)P(B)\).