Numpy常见数学运算

Numpy常见数学运算

导入库

import numpy as np 

在二维坐标系常见操作

#创建两个数组
a = np.array([1,2])
b = np.array([3,4])
a,b

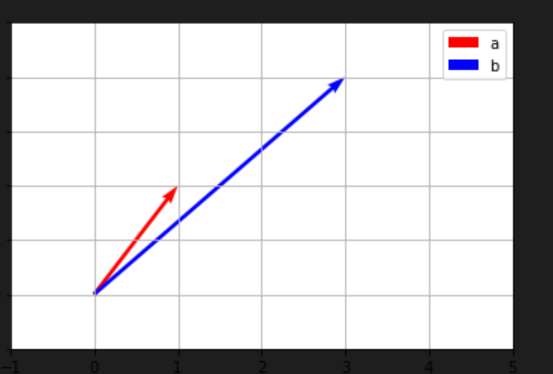
#绘制这两个向量
import matplotlib.pyplot as plt
fig,ax=plt.subplots()
#绘制从[0,0]到[2,2]的向量
pa=ax.quiver(0, 0, 1, 2, angles='xy', scale_units='xy', scale=1, color="red",label='a')
pb=ax.quiver(0, 0, 3, 4, angles='xy', scale_units='xy', scale=1, color="blue",label='b')
ax.set_xlim([-1, 5])
ax.set_ylim([-1, 5])
ax.legend()
ax.grid(True)

plt.show()

# 两个向量之差 , 也就是对应元素之差 
# 向量之差依然是向量，正负代表方向
b-a ,a-b

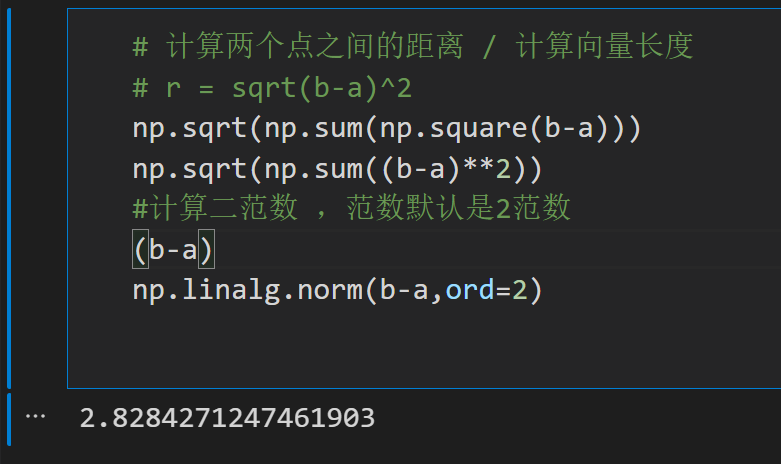
# 计算两个点之间的距离 / 计算向量长度
# r = sqrt(b-a)^2
np.sqrt(np.sum(np.square(b-a)))
np.sqrt(np.sum((b-a)**2))
#计算二范数 ，范数默认是2范数
(b-a)
np.linalg.norm(b-a,ord=2)

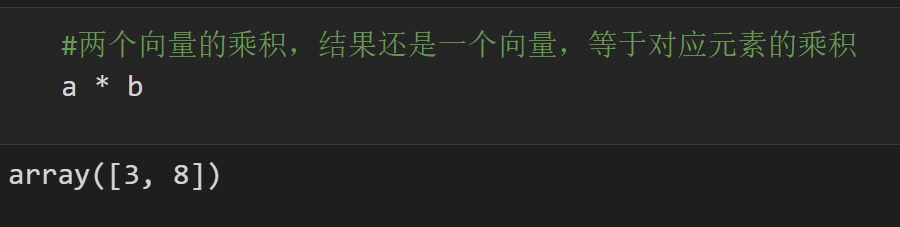
#两个向量的乘积，结果还是一个向量，等于对应元素的乘积
a * b 

# 计算两个向量的点乘，结果是一个数值（标量），等于对应元素相乘再相加
np.dot(a,b)

# 计算两个二维向量的叉积（外乘） , 二两向量围成的平行四边形的面积(有向面积)，这个与行列式的几何意义保持一致
# 方向是
np.cross(a,b) # 方向为负，顺时针
np.cross(b,a) # 方向为正，逆时针

# 计算两个向量之间的夹角 ，
# 根据点乘（内积）定义 :向量a 点乘 向量b = 向量a的模 乘以 向量b的模 乘以 cos theta 
# 几何
# cos theta = 向量a 点乘 向量b  /   向量a的模 乘以 向量b的模
cos_radian =  np.dot(a,b) / (np.linalg.norm(a) * np.linalg.norm(b) )
cos_radian
#由夹角的余弦值计算夹角的大小
radian = np.arccos(cos_radian) # arccos结果为[0,pi]的弧度制
radian
# 将弧度变为角度
angle = np.rad2deg(radian)
angle
# 由夹角（弧度）计算cos值
np.cos(radian)

# 计算向量与x轴的夹角(弧度制)
radian1 = np.arctan(a[1]/a[0])  #1 先利用坐标计算tan = y/x
angle1 = np.rad2deg(radian1)   #将弧度制转为角度

radian2 = np.arctan2(a[1],a[0]) # 使用 arctan2 ，直接根据坐标计算 ， 注意坐标顺序

radian1,radian2

三维平面

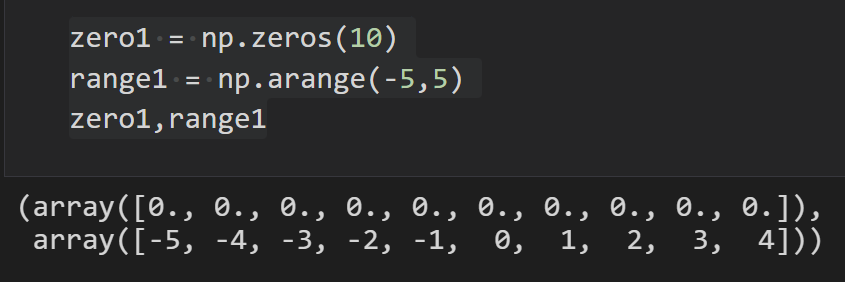
zero1 = np.zeros(10)
range1 = np.arange(-5,5)
zero1,range1

# 三维坐标绘制箭头
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig=plt.figure()
ax = fig.add_subplot(111, projection='3d')
plt.grid(ls='--')
#绘制坐标轴
ax.plot(zero1,zero1,range1,color="black")
ax.quiver(0, 0,0, 0, 0,5,  color="black")
ax.plot(zero1,range1,zero1,color="black")
ax.quiver(0, 0,0, 0, 5,0,  color="black")
ax.plot(range1,zero1,zero1,color="black")
ax.quiver(0, 0,0, 5, 0,0,  color="black")
#绘制从[0,0]到[2,2]的向量
ax.quiver(0, 0,0, 1, 1,1,  color="red",label='a')
ax.quiver(0, 0,0, 2, 3, -3,   color="blue",label='b')
ax.quiver(0, 0,0, -2,- 3, 4,   color="green",label='c')
ax.set_xlim([-5, 5])
ax.set_ylim([-5 , 5])
ax.set_zlim([-5,5])
ax.legend()
plt.show()

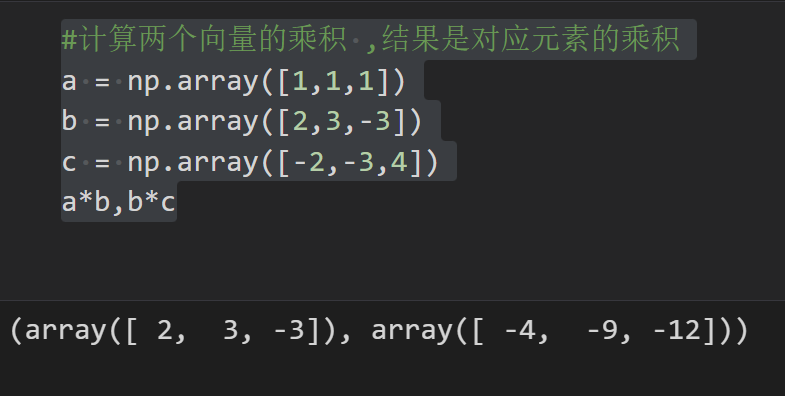
#计算两个向量的乘积 ,结果是对应元素的乘积
a = np.array([1,1,1])
b = np.array([2,3,-3])
c = np.array([-2,-3,4])
a*b,b*c

# 计算向量的差
b-a

# 计算两个点之间的距离 / 计算向量长度
# r = sqrt(b-a)^2
t1 = np.sqrt(np.sum(np.square(c)))
t2 = np.sqrt(np.sum((c)**2))
#计算二范数 ，范数默认是2范数
t3 = np.linalg.norm(c,ord=2)
(t1,t2,t3)

# 计算两个向量的点乘，结果是一个数值（标量），等于对应元素相乘再相加
np.dot(a,b)

# 计算两个三维向量的叉积（外乘） , 结果是一个向量，他是向量a,b组成的平面的法向量
t1= np.cross(a,b) #  法向量的方向，根据左手定则
t2 = np.cross(b,a) #
# 验证法向量 ,结果为0 说明向量t与a,b垂直
np.dot(a,t1)
np.dot(b,t1)
t1,t2
# 求单位法向量 ，也就是向量/向量的模
t = t1 /np.linalg.norm(t1,ord=2)
t1,t*np.linalg.norm(t1,ord=2)

"三维图中绘制由任意两个三维向量组成的平面"
#向量分为为a=(1,1,1),b=(2,3,-3)
#则设所在平面的方程为（X,Y,Z=a1*X+a2*Y）
#将两个向量的坐标带入，求解a1,a2
#这里的X,Y是指绘图区域(X*Y)

fig=plt.figure()
ax = fig.add_subplot(111, projection='3d')
plt.grid(ls='--')
#绘制从[0,0]到向量
ax.quiver(0, 0,0, 1, 1,1,  color="red",label='a')
ax.quiver(0, 0,0, 2, 3, -3,   color="blue",label='b')
ax.quiver(0, 0,0, -6,5, 1,   color="yellow",label='t1')
ax.quiver(0, 0,0, 6,-5, -1,   color="green",label='t2')
#绘制平面
x = np.linspace(0,1,10)
y = np.linspace(0,1,10)
X,Y = np.meshgrid(x,y)
a1= 6 
a2=-5
Z= a1*X+a2*Y
surf = ax.plot_surface(X,Y,Z,color='yellow')
#绘制坐标轴
ax.plot(zero1,zero1,range1,color="black")
ax.quiver(0, 0,0, 0, 0,5,  color="black")
ax.plot(zero1,range1,zero1,color="black")
ax.quiver(0, 0,0, 0, 5,0,  color="black")
ax.plot(range1,zero1,zero1,color="black")
ax.quiver(0, 0,0, 5, 0,0,  color="black")
ax.set_xlim([-5, 5])
ax.set_ylim([-5 , 5])
ax.set_zlim([-5,5])
ax.legend()
plt.show()

# 计算两个向量之间的夹角 ，
# 根据点乘（内积）定义 :向量a 点乘 向量b = 向量a的模 乘以 向量b的模 乘以 cos theta 
# 几何 cos theta = 向量a 点乘 向量b  /   向量a的模 乘以 向量b的模
cos_radian =  np.dot(a,b) / (np.linalg.norm(a) * np.linalg.norm(b) )

#由夹角的余弦值计算夹角的大小
radian = np.arccos(cos_radian) # arccos结果为[0,pi]的弧度制

# 将弧度变为角度
angle = np.rad2deg(radian)

# 由夹角（弧度）计算cos值
t = np.cos(radian)
cos_radian,radian,angle,t

#计算向量与平面的夹角