扩展—— 向量矩阵张量
扩展——向量矩阵张量
参考
【科普向/中英字幕】What's a Tensor? 张量简介_哔哩哔哩_bilibili
- 标量就是数值,几何含义为数轴上的线段的长度
- 向量(矢量)有着方向和大小,其几何含义为带有箭头的一个线段
- 矩阵是一个二维的表,其几何含义为空间基的变换
- 张量
上面最浅显的认识,实际上这几个量在数学(代数和几何),计算机,物理学科上有着不同的理解。
物理角度来描述矢量和张量
矢量
在物理中,矢量是一个带箭头(方向)的线段(长度)。我们在高中的时候,对物体进行受力分析的时候会用到。
在物理中,矢量是不依赖于坐标系存在的,
- 首先,它在同一个坐标系下可以随意移动。
- 第二,如果我们更换坐标系,那么会给予这个矢量不同的描述方式,但是这个矢量本身的长度和方向是不会发生变化的。
矢量除了可以描述力,还可以用来描述很多东西。
例如,我们可以用矢量描述一个空间中某个二维平面的面积,我们使矢量的长度和面积成比例,然后矢量的箭头和这个平面的法向量一致,这样我们就用矢量清晰明确简单地描述出了一个二维平面的面积。(ps,这个平面和数学中的平面含义不同,数学中的平面是抽象的没有大小的。)(ps:这段话中的二维平面面积可以理解为你桌面上的一张A4纸,然后你把一支笔垂直放在上面,这样通过描述笔我们就能相应确定出这张a4纸)
矢量的描述与坐标系
我们可以建立一个坐标系,例如熟悉的笛卡尔坐标系。
当坐标系确定,我们也随之确定了单位向量,其方向与坐标轴正向相一致,长度是1(这是数学中抽象的1)。
矢量的分量分解
- 物理中的矢量是可以随意移动位置的(这和数学的概念有很大差别)。
- 我们想要对一个矢量进行分解,我们可以将这个矢量移动到坐标原点,或者直接在矢量所在的地方建立一个坐标系。
- 然后我们根据坐标系的单位向量,对这个矢量做投影,就能得到在我们所建立的坐标系下通过分量对矢量的描述。
- 这个过程实际上就是我们高中时候画的矩形或者平行四边形对力的分解。
对矢量的分解完成后,我们就到了依赖于我们的单位向量对这个矢量的描述。这个描述和矢量的本身是一致的。(好比说,你有个同学叫王二,但朋友们一致喊他老王。那么这个老王就是在你们的视角下对他的描述。不管你喊老王还是王二,大家(这群朋友)都知道就是这个人。而且这群朋友就不需要喊他王二,喊老王就可以了)
我们有一个矢量 ,我们可以在笛卡尔三维坐标系下进行分解为, 然后我们把这三个写在一起加个括号就成为了行向量(或列向量) ,这样我们有三个指标(单位向量),就把这个矢量分解成了对应三个结果。
像这样的矢量就又叫做一阶张量。这里的一阶指的是每一个分量只对应一个指标。
同样,标量可以看作是0阶张量。因为标量是没有方向的,所以他也就不需要在不同方向上的分量。这里的0阶理解为分量对应着0个指标。
举一个高阶向量的例子,比如一个三维空间的二阶向量。

是的,这时候一个元素会在9个基矢上面分解为9个分量,每一个分量有着两个指标
其代表的物理含义为内部受的力(我物理不大好),-每个分量的两个指标分别代表所在平面的方向和所收到力及方向,比如表示在平面收到方向的力,表示在平面收到方向的力,表示在平面收到方向的力 ;这样我们能够用一个向量来表示面(面的法向量就是矢量方向,面的大小就是长度),另一个向量表示受到的力(长度+方向)。
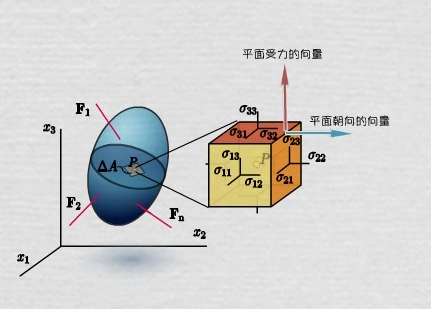
我们再来看一个三维空间中的三阶张量。


是的,在三维空间中,有着27组基矢量,27个分量,每一个分量有着3个指标
使用分量和基矢量通过张量的方式来描述的原因是什么呢?
不同的观测者有着不同的参照系,因为不同的参照系下,描述同一个物体,大家的基矢量不同,那么描述结果(对应的分量)也就不同 。(比如,斗气和真气和能量)
但是如果我们在描述的时候带上我们的坐标系,大家就能够更好的理解。(附带基本样本,最小单元)更一般的,在不同的参照系下,描述的物体的某些属性是不变的,当大家都带上坐标系后,描述的结果就成了一致的。(好神奇)
但或许没法做到上面的结果,但我们也能发现如果我们的基矢量在不同的参照系之间存在着某些联系,更准确的说存在一种变换规则(比如三天的真气=一天的斗气=1000焦耳)(比如过渡矩阵),那么我们描述的结果也存在相应变换规则(元婴期=斗宗=喷气式飞机),那么我们的分量和矢量的组合的描述方式对于所有的观测者都是一样的。
这也是张量不需要参照系的原因,这是因为它在描述的过程中显示地附带上了所使用的基矢量。
数学角度
几何角度的理解可以参见我之前对高代的回顾。
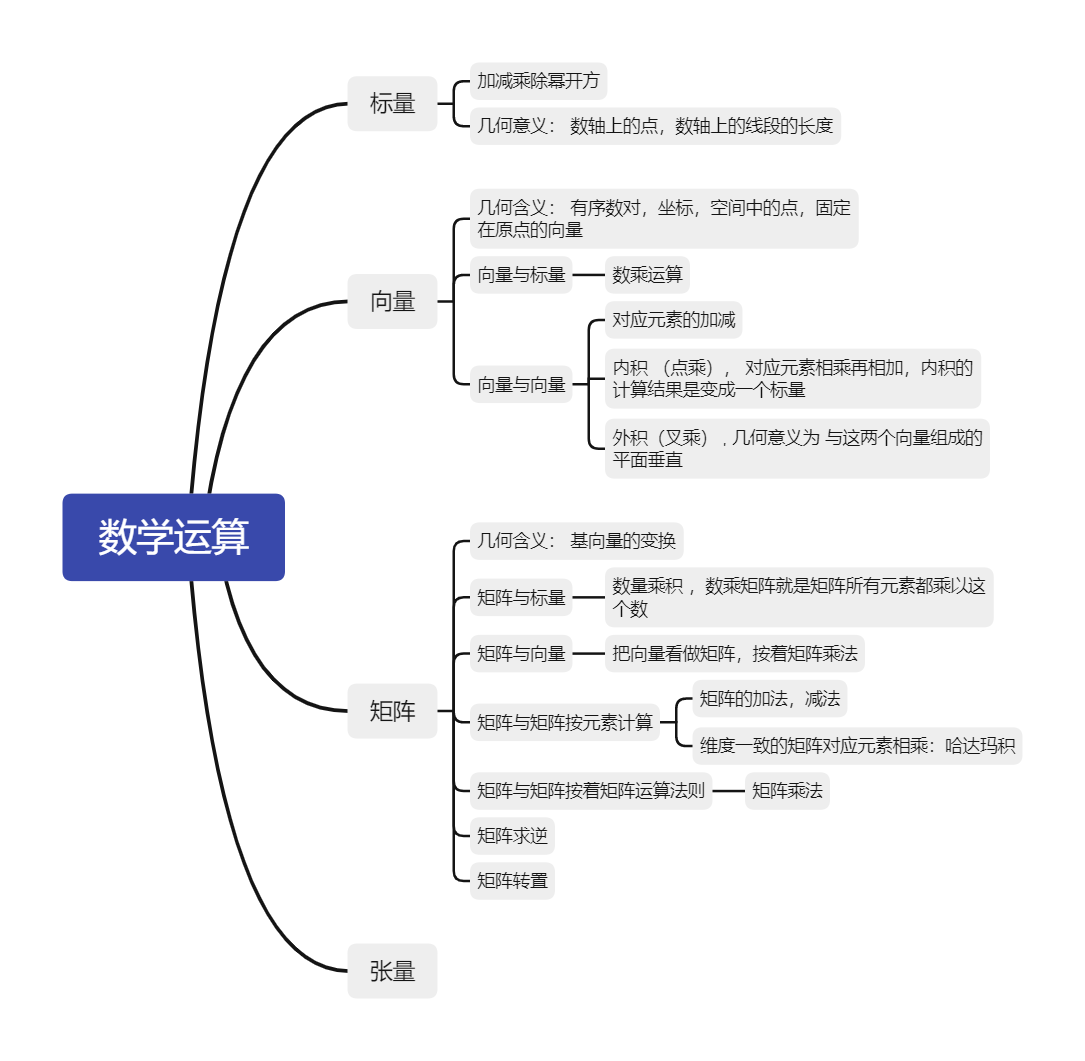
标量
- 几何意义为数字 ,数轴上的点 ,数轴上的线段长度 。但其就是一个抽象的数字。
- 运算就是我们熟悉的数值运算
向量
向量依赖于坐标系(基向量)
- 几何含义
在这一系列可以相互转化的概念中,基向量是最核心的概念,正是由于基向量,我们给我们搭建了从空间到数字的桥梁。
- 向量运算,相同维度的向量可以直接对应元素的运算 ,也就是把它看成标量的列表 ,加减乘除都是对应位置的标量的运算。应该说是基向量统一后,在基向量上的数值运算
- 可以把向量看做成矩阵形式 ,运算规则就是矩阵的运算 ,
矩阵
矩阵的几何含义是 基向量的线性变换 ,向量左乘一个矩阵就得到了在新的基下的坐标 ,这个矩阵的组成恰好是新的基向量在原来基下的坐标。
首先,我们找到了新的基在原来的基的坐标,我们把这个坐标放在一起组成了一个矩阵
这个矩阵第一列的元素是新基在下的坐标,第二列的元素是新基的在下的坐标
这个矩阵就描述了基之间的变换关系
我们也需要明确,两个不同的坐标只是同一个向量空间不同参照系对同一个物体的描述,我们不妨设两个坐标分别是
这样我们有
这样将其带入,我们就得到在同一坐标系下对这个物体的描述,
这个式子,就说明如果在基下我们对某个物体有一个描述,然后我们想要得到在原来的基下对这个物体的描述,我们只需要左乘这个矩阵即可。
那么反过来。我们在原来的基下我们对某个物体有一个描述 ,我们想要得到在新的基下对这个物体的描述,我们只需要左乘这个矩阵的逆即可。
在整个过程中,矩阵充当了一组基到另一组基的桥梁,我们称之为过渡矩阵。
而且这个过渡事实上就是可逆的。
对于矩阵的运算我们有
张量
基础篇4:张量的运算及矢量梯度、张量散度 - 知乎 (zhihu.com)
计算机角度
在计算机中,向量,矩阵,张量 其实都是多维数字列表的概念。在python中就是元组tuple(不可比序列)和列表list(可修改数据项的序列)。
数据的维度
维度:一组数据的组织形式
一维数据:一维数据由对等关系的有序或无序数据构成,采用线性方式组织,对应列表、数组和集合等概念
列表和数组 区别:列表的数据类型可以不同,数组的数据类型相同
二维数据: 二维数据是有多个一维数据构成,是一维数据的组合形式。表格是典型的二维数据,其中,表头是二维数据的一部分
多维数据:多维数据有一维或二维在新维度上扩展而成
高维数据:高维数据仅利用最基本的二元关系展示数据间的复杂结构。
数据维度的Python展示
数据维度是数据的组织形式
一维数据:列表和集合类型
二维数据:列表类型
多维数据:列表类型
高维数据:字典类型或数据表示格式JSON、XML、YAML格式
在python中常用得到的包有 numpy , tensor。
广播法则
广播法则来源于numpy,它的定义如下:
- 让所有输入数组都向其中shape最长的数组看齐,shape中不足部分通过在前面加1补齐
- 两个数组要么在某一个维度的长度一致,要么其中一个为1,否则不能计算
- 当输入数组的某个维度的长度为1时,计算时沿此维度复制扩充×一样的形状
torch当前支持自动广播法则,但更推荐使用以下两个方法进行手动广播,这样更直观,更不容出错:
- unsqueeze或view:为数据某一维的形状补1
- expand或expand_as:重复数组,实现当输入的数组的某个维度的长度为1时,计算时沿此维度复制扩充成一样的形状
注:repeat与expand功能相似,但是repeat会把相同数据复制多份,而expand不会占用额外空间,只会在需要的时候才扩充,可以极大地节省内存。
python
a = t.ones(3, 2)
b = t.zeros(2, 3, 1)
自动广播法则:
- a是二维,b是三维,所在现在较小的a前面补1(等价于
a.unsqueeze(0),a的形状变成(0,2,3)) - 由于a和b在第一维和第三维的形状不一样,利用广播法则,两个形状都变成了(2,3,2)
a + b
tensor([[[1., 1.],
[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.],
[1., 1.]]])
对上述自动广播可以通过以下方法实现手动广播
python
a.unsqueeze(0).expand(2, 3, 2) + b.expand(
2, 3, 2) # 等价于a.view(1,3,2).expand(2,3,2) + b.expand(2,3,2)
numpy
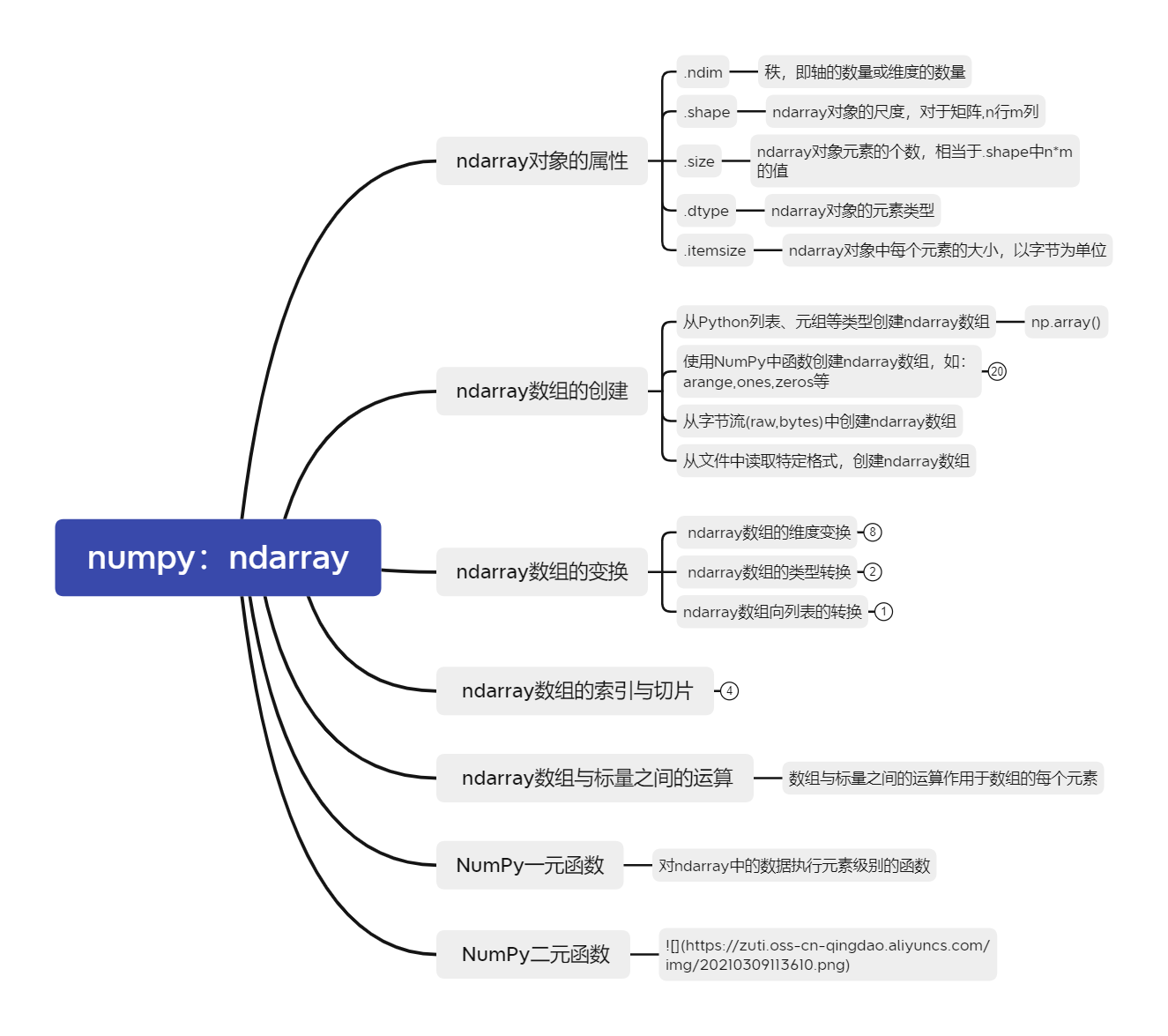
tensor
本文来自博客园,作者:{珇逖},转载请注明原文链接:https://www.cnblogs.com/zuti666/p/16095601.html



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY