我理解的高等代数——2坐标系变换与矩阵

2 坐标系变换与矩阵

在第一弹中，我们简单介绍了线性空间，并留下了一个问题，那就是我们选定不同的基向量和坐标系，对物体的描述会带来什么影响，不同的坐标系之间的关联又是怎样的呢？

首先，毫无疑问的是，当我们选定一组新的基向量之后，同一个物体，在不同的坐标系下有了不同的描述结果。

橙色的坐标系虽然看起来有些奇怪，但是毫无疑问它的确是一个坐标系，因为他能够把这个二维平面中的所有点都表示出来。

好了我们有了这两个坐标系，那我们想问的是在橙色的坐标系下，对这个蓝色小圆的描述是怎样的呢？

我们不妨先将这个小球在橙色坐标系下的位置设为[x,y] 。

值得注意的是，在两个坐标系下的数值倏然不同，但是我们描述的依然是同一个物体。就是这个蓝色小球，而不是其他的三角形等物体。

另外一个值得注意的是，这两个坐标系的原点是一致的，也就是说这个变化并没有改变原点的位置。

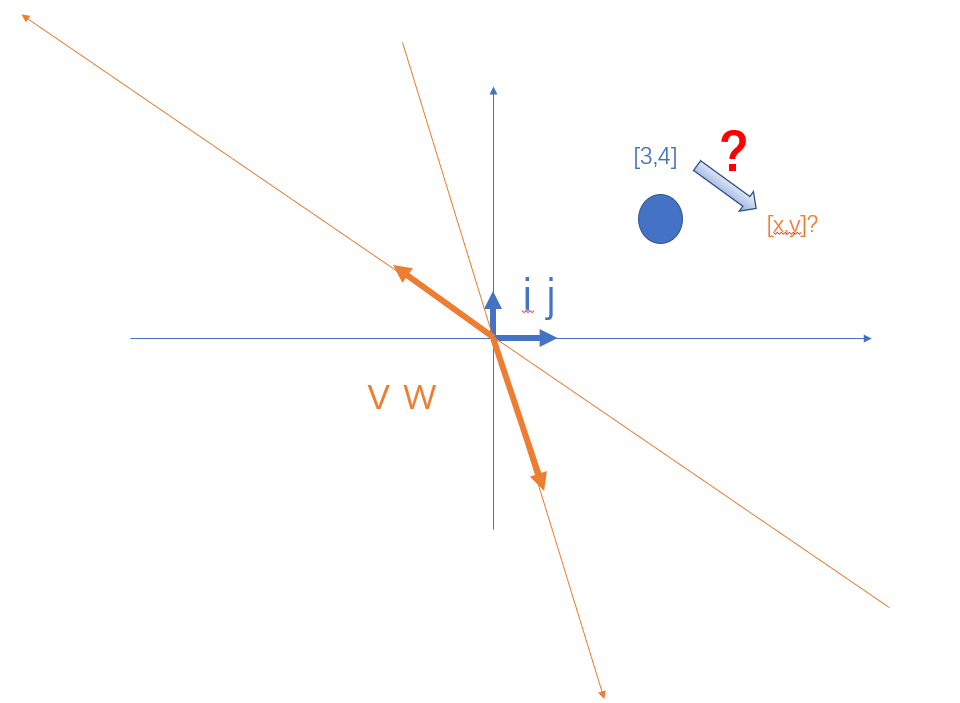
那么又产生了一个新的问题，从蓝色坐标到黄色坐标的变换时怎样的呢？

记得上次我们所说的从空间到数值的关键桥梁是什么吗？对就是基向量，让我们从基向量的角度来看一看这个变换过程。

那为什么要这么做呢，让我们来看

我们有

\[\overrightarrow{ \left[ \begin{array}{1} 3\\ 4 \end{array} \right ] } = \left[ \begin{array}{1} 3\\ 4 \end{array} \right ] \left( \begin{array}{1} \overrightarrow{i}\\ \overrightarrow{j} \end{array} \right) =(3,4) =3 \overrightarrow{i}+ 4\overrightarrow{j} \\ =[i,j] \left[ \begin{array}{1} 3\\ 4 \end{array} \right ] =[3,4] \left[ \begin{array}{1} i\\ j \end{array} \right ] \\ \overrightarrow{ \left[ \begin{array}{1} x\\ y \end{array} \right ]} = \left[ \begin{array}{1} x\\ y \end{array} \right ] \left( \begin{array}{1} \overrightarrow{v}\\ \overrightarrow{w} \end{array} \right ) =(x,y) = x \overrightarrow{v} + y\overrightarrow{w} \\ =[v,w]\left[ \begin{array}{1} x\\ y \end{array} \right ] =[x,y]\left[ \begin{array}{1} v\\ w \end{array} \right ] \\ \]

注意，在上面的式子中，第一个是向量乘法，也就是对应元素直接相乘；后面的是矩阵乘法 ，

我们发现，向量乘法总是可以用矩阵乘法来进行表达，而且把它写作行向量和列向量并没有任何区别，只是我们的习惯而已。

在这里我们可以回顾一下，上一篇文章的内容，我们可以将向量理解为对基向量的伸缩 ，

实际上这只不过是在两个不同的视角下描述的同一物体，于是我们有

\[[i,j]\left[ \begin{array}{1} 3\\ 4 \end{array} \right ] =[v,w]\left[ \begin{array}{1} x\\ y \end{array} \right ] \]

这两个坐标的数值是根据基向量的变化来的，所以根本的原因是坐标系的变化，也就是基向量的变化。那么我们只需要找出这两个基向量的变化过程，然后我们就能得到相应的向量的结果。

基变换

那我们怎样来找这个基向量的变化呢？

首先，我们在基向量\(i,j\)形成的坐标下来看这个基向量的变化过程 ， 我们可以看到这时候在我们的蓝色坐标系下，橙色的两个基向量能够使用\(i,j\)来表述出来 ，我们不妨设\(i,j\)为\(1,1\) ,\(v,w\)为\((-3,2),(1,-4)\)

我们有

\[\overrightarrow{ \left[ \begin{array}{1} v\\ w \end{array} \right ] } = \left[ \begin{array}{1} -3\overrightarrow{i}+2\overrightarrow{j}\\ \overrightarrow{i}-4\overrightarrow{j} \end{array} \right ] \\ \left[ \begin{array}{1} v\\ w \end{array} \right ] = \left( \begin{array}{1} -3, & 2\\ 1 , &-4 \end{array} \right ) \left[ \begin{array}{1} i\\ j \end{array} \right ] \\ [v,w] =[i,j] \left( \begin{array}{1} -3, & 1\\ 2 , &-4 \end{array} \right ) \]

同样，上面是向量乘法，下面是矩阵乘法。但是其表达的含义是一样的，只不过数学规范定义的运算不一样而已。

第二个式子，我们把向量写作列向量的形式 ；第三个式子，我们把向量写成了行向量的形式。

记这个矩阵为\(A\) ，我们来观察一下这个矩阵，

在第二个式子中，左端是我们新的一组基，右边是原来的一组基 ， 矩阵中，第一行的元素就是\(v\)在\(i,j\)下的坐标，第二行的元素就是w在\(i,j\)下的坐标。

我们就得到了从基\(i,j\)到基\(v,w\)变换的矩阵 ，

坐标变换

我们将上面基变换的矩阵带入等式，于是就能得到

\[[i,j]\left[ \begin{array}{1} 3\\ 4 \end{array} \right ] =[v,w]\left[ \begin{array}{1} x\\ y \end{array} \right ] \\ [v,w] =[i,j] \left( \begin{array}{1} -3, & 1\\ 2 , &-4 \end{array} \right ) \\ [i,j]\left[ \begin{array}{1} 3\\ 4 \end{array} \right ]= [i,j] \left( \begin{array}{1} -3, & 1\\ 2 , &-4 \end{array} \right ) \left[ \begin{array}{1} x\\ y \end{array} \right ] \]

这样，我们就得到了在同一坐标系下的描述，因为\([i,j]\)是基向量，也就是单位向量，于是我们有

\[\left[ \begin{array}{1} 3\\ 4 \end{array} \right ]= \left( \begin{array}{1} -3, & 1\\ 2 , &-4 \end{array} \right ) \left[ \begin{array}{1} x\\ y \end{array} \right ] \]

我们就能求出\([x,y]\)的坐标那就是

\[\left( \begin{array}{1} -3, & 1\\ 2 , &-4 \end{array} \right )^{-1} \left[ \begin{array}{1} 3\\ 4 \end{array} \right ]= \left[ \begin{array}{1} x\\ y \end{array} \right ] \]

上面这个式子就描述了两个不同坐标系下，描述同一物体的坐标关系。其中，最关键的就是两个基向量变换的矩阵。通过这个矩阵，不但描述了基向量之间的变换关系，还表述了坐标之间的关系。我们看到坐标的变换关系和基向量的变换关系是一致的。

\[\left( \begin{array}{1} -3, & 1\\ 2 , &-4 \end{array} \right )^{-1} \left[ \begin{array}{1} v\\ w \end{array} \right ]= \left[ \begin{array}{1} i\\ j \end{array} \right ] \]

同时，我们来观察这个式子，我们发现这个矩阵里的元素就是向量\([v,w]\)在基\([i,j]\)下的坐标\([-3,2],[1,4]\)

回顾

首先，我们找到了新的基\([v,w]\)在原来的基\([i,j]\)的坐标\((a,b),(c,d)\)，我们把这个坐标放在一起组成了一个矩阵\(A\)

\[A = \left( \begin{array}{1} a, & c\\ b , &d \end{array} \right ) \]

这个矩阵第一列的元素是新基\(v\)在\([i,j]\)下的坐标，第二列的元素是新基\(w\)的在\([i,j]\)下的坐标

这个矩阵\(A\)就描述了基之间的变换关系

\[[v,w] =[i,j] A \]

我们也需要明确，两个不同的坐标只是同一个向量空间不同参照系对同一个物体的描述，我们不妨设两个坐标分别是

\[\left[ \begin{array}{1} x_1\\ x_2 \end{array} \right ] \left[ \begin{array}{1} x_1'\\ x_2' \end{array} \right ] \]

这样我们有

\[[v,w] \left[ \begin{array}{1} x_1'\\ x_2' \end{array} \right ]= [i,j]\left[ \begin{array}{1} x_1\\ x_2 \end{array} \right ] \]

这样将其带入，我们就得到在同一坐标系下对这个物体的描述，

\[[i,j]A \left[ \begin{array}{1} x_1'\\ x_2' \end{array} \right ]=[i,j]\left[ \begin{array}{1} x_1\\ x_2 \end{array} \right ] \]

这个式子，就说明如果在基\([v,w]\)下我们对某个物体有一个描述\((x'_1,x'_2)\),然后我们想要得到在原来的基\([i,j]\)下对这个物体的描述，我们只需要左乘这个矩阵\(A\)即可。

那么反过来。我们在原来的基\([i,j]\)下我们对某个物体有一个描述\((x_1,x_2)\) ,我们想要得到在新的基\([v,w]\)下对这个物体的描述,我们只需要左乘这个矩阵\(A\)的逆即可。

\[\left[ \begin{array}{1} x_1'\\ x_2' \end{array} \right ] = A^{-1} \left[ \begin{array}{1} x_1\\ x_2 \end{array} \right ] \]

在整个过程中，矩阵\(A\)充当了一组基到另一组基的桥梁，我们称之为过渡矩阵。

而且这个过渡事实上就是可逆的。

但等等，我们将两个基向量进行变换，一般的情形时是我们得到了一个类似的坐标系，但还有别种情况就是

• 我们把两个基向量变到了同一条线上，也就是变换后的维度降低了，那么在这种情形下，这个矩阵就相当于我们对这个二维空间向一维空间做了一次投影，这样的映射结果就是多对一
• 我们左乘一个\(3 \times 2\)维度的矩阵，得到结果是一个有着三个元素的向量，这就是被映射到了高维度的三维空间 ， 这种映射结果可能是一对多 ，也就是上面描述降维的反过程升维

特征值与特征向量

在坐标系变换的时候，大多数向量在新的坐标系下的方向和长度都发生了变化。但是有一些向量只是长度发生了变化，但是方向没有变。我们把这些方向没有变化的向量称之为特征向量，把长度变化的比例称之为特征值。

\[A \xi = \lambda_0 \xi \]

含义：为什么要用到这个概念呢，因为特征值的奇特之处就在于整个空间的变换并没有影响到它的方向，这是不简单的。类似于，王朝更替，但大家还是学习儒学，所以这个不变的儒学就代表着某些含义。