朴素贝叶斯

朴素贝叶斯

目录

• 朴素贝叶斯
• 贝叶斯公式
• 朴素 — — 条件独立性假设
• 三步走
  • 先验概率分布
  • 条件概率
  • 后验概率计算
    • 后验概率最大化的理解
• 朴素贝叶斯的参数估计
  • 极大似然估计
  • 贝叶斯估计
• 示例 以李航统计学习方法P63 例4.1下的表4.1为例，来确定\(x=(2,S)^T\)的标签\(y\)
  • 1 极大似然估计法
  • 2 贝叶斯估计法
• 优缺点
• 常用模型
  • 伯努利朴素贝叶斯
    • 代码实现
  • 多项式朴素贝叶斯
    • 使用情形
    • 代码实现
  • 高斯朴素贝叶斯
    • 代码实现

贝叶斯公式

我们可以将\(P(\theta |X)\)​进行贝叶斯概率进行展开

\[P(\theta | X) = \frac{ P(X| \theta)}{ P(X)} \cdot P(\theta) \ \ \ (2) \]

上式中$ P (\theta|X)$​​​称作​后验概率 ， \(P(\theta)\)​称作先验概率。\(P(X|\theta)\)叫做似然度，\(P(X)\)是边缘概率，与待估计参数\(\theta\)​​无关，又叫做配分函数。

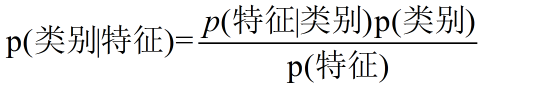
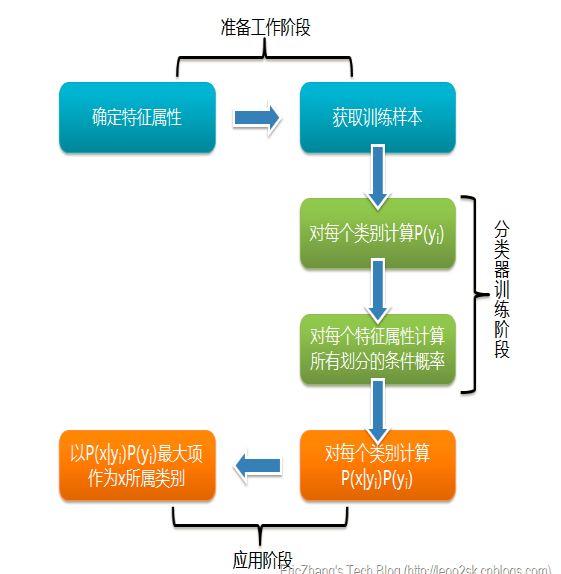
朴素 — — 条件独立性假设

三步走

先验概率分布

先验概率分布就是说在训练样本中，不同类别占的比例\(P(Y=c_k),k=1,2\cdots,K\)

条件概率

条件概率分布就是指，在某一类别下，不同特征占的比例

\[P(X=x|Y=c_k)=P(x^{(1)}=x^{(1)},\cdots,X^{(n)}=x^{(n)}|Y=c_k),k=1,2,\cdots,K \]

我们可以按着条件概率对其展开

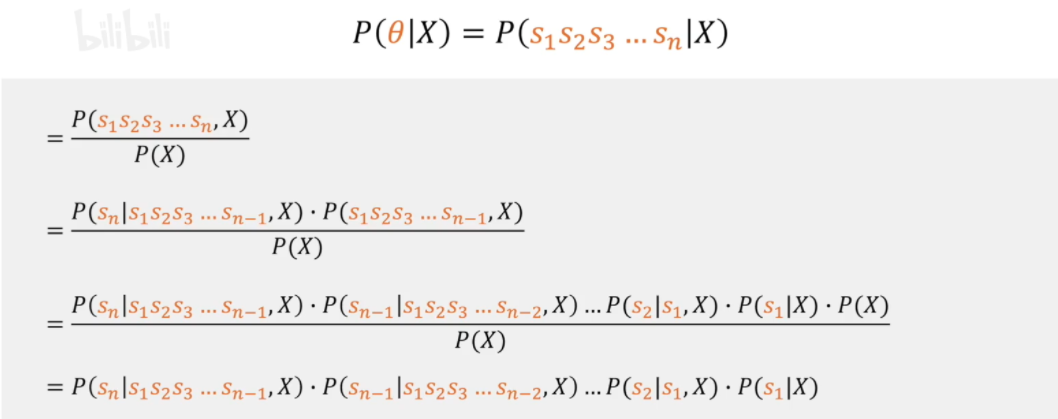
我们发现这就需要计算不同特征之间的条件概率，是很麻烦的

朴素贝叶斯法对概率条件分布做了条件独立的假设,这是一个很强的假设

这样，条件概率就成为了不同特征\(s_n\)在类别\(X\)下的条件概率的乘积，即

\[\begin{aligned} P(X=x|Y=c_k) &=P(x^{(1)}=x^{(1)},\cdots,X^{(n)}=x^{(n)}|Y=c_k) \\ &=\prod_{j=1}^n P(X^{(j)=x^{(j)}}| Y=c_k) \end{aligned} \]

也就是我们得到了联合概率分布\(P(X|Y)\)​

后验概率计算

朴素贝叶斯分类时，对于给定的输入\(x\)​,通过学习后的模型计算后验概率分布\(P(Y=c_k|X=x)\)，将后验概率最大的类作为\(x\)的输出。即计算

\[P(可能的类别c_i|输入样本的特征x) \]

然后将结果最大的那个类别\(c_i\)​作为输入样本\(x\)的分类结果。

后验概率的计算：

根据贝叶斯定理

\[\begin{aligned} P(Y=c_k |X=x) &= \frac{P(X=x|Y=c_k)P(Y=c_k)}{P(X=x)} \\ &=\frac{P(X=x|Y=c_k)P(Y=c_k)}{\sum_kP(X=x|Y=c_k)P(Y=c_k)} \\ \text{将条件独立性假设带入} \\ &= \frac{P(Y=c_k) \prod_j P(X^{(j)}=x^{(j)}|Y=c_k)}{\sum_kP(Y=c_k)\prod_j P(X^{(j)}=x^{(j)}|Y=c_k)} ,k=1,2,\cdots,K \end{aligned} \]

这是朴素贝叶斯分类的基本公式，于是，朴素贝叶斯分类器可以表示为

\[y=f(x)=arg\ \underset{c_k}{max} \frac{P(Y=c_k) \prod_j P(X^{(j)}=x^{(j)}|Y=c_k)}{\sum_kP(Y=c_k)\prod_j P(X^{(j)}=x^{(j)}|Y=c_k)} \]

注意到，上式中分母对所有的\(c_k\)是相同的，所以

\[y=f(x)=arg\ \underset{c_k}{max} {P(Y=c_k) \prod_j P(X^{(j)}=x^{(j)}|Y=c_k)} \]

朴素贝叶斯将样本分到后验概率最大的类别中。

后验概率最大化的理解

朴素贝叶斯将样本分到后验概率最大的类别中。这等价于期望风险最小化。

朴素贝叶斯的参数估计

根据上面我们知道朴素贝叶斯分类分三步走，分别是先验概率计算，条件概率计算，后验概率计算。那么我们先需要计算出来先验概率和条件概率，但是我们只是从样本中得到，也就是说我们根据样本来估计整体的先验概率和条件概率。从样本估计整体就有两种思路，即统计主义和贝叶斯主义。下面我们分别介绍。

极大似然估计

其实在我们计算先验概率分布，就很自然会有下面的想法：

\[P(\text{类别}c_k)=\frac{\text{类别}c_k\text{的数量}}{\text{样本总数}} \]

这背后的想法就是频率派的极大似然估计思想。我们认为从统计数据中得到的分布就是真实数据的分布，不需要有先验知识。

先验概率的极大似然估计：

\[P(Y =c_k) = \frac{\sum_{i=1}^N I(y_i=c_k)}{N},k=1,2,\cdots,K \]

这其实就是上面的式子，和我们自然的想法是一致的。

自然，我们同样会有条件概率的极大似然估计

\[P(X^{(j)}=a_{jl}|Y=c_k) = \frac{\sum_{i=1}^NI(x^{(j)}_i=a_{jl},y_i=c_k)}{\sum_{i=1}^NI(y_i=c_k)} \\ j=1,2,\cdots,n;l=1,2,\cdots,S_j;k=1,2,\cdots,K \]

通俗的表示就是

\[P(特征a_{ji}|类别c_k)=\frac{类别为c_k的样本中特征为a_{ji}的样本的数量}{类别为c_k的样本总数} \]

贝叶斯估计

在上面的极大似然估计，很符合我们的直觉。但是应该注意到极大似然估计方法可能会出现要统计的概率值为0的情况，这时候会影响到后验概率的计算，使分类产生误差。解决这一问题的方法是采用贝叶斯估计。

我的直观的想法也就是在分子上面强行加一个整数，使得结果不会为0。

我们来看公式，看看人家是怎么处理的

先验概率的贝叶斯估计：

\[\begin{aligned} P_\lambda (Y=c_k) &= \frac{\sum_{i=1}^NI(y_i=c_k)+\lambda}{N+K\lambda} \\ P_\lambda(\text{类别}c_k) &= \frac{\text{类别}c_k\text{的数量}+\lambda}{\text{样本总数}+类别数量 \times\lambda} \\ \lambda \geq 0 \end{aligned} \]

这个分母为什么是\(N+ K\lambda\)呢？其实很显然，我们在每一个类别\(c_k\)都加上了\(\lambda\) ,所以对于\(K\)个类别，样本的总量增加了\(K \lambda\)。我们就用我们修正后的类别数量和总量来计算先验概率。

条件概率的贝叶斯估计：

\[P_\lambda(X^{(j)}=a_{ji}|Y=c_k)=\frac{\sum_{i=1}^NI(x^{(j)}_i=a_{jl},y_i=c_k)+\lambda}{\sum_{i=1}^NI(y_i=c_k)+S_j\lambda} \\ \text{其中,对任何}l=1,2,\cdots,S_j,k=1,2,\cdots,K\text{有} \\ P_\lambda(X^{(j)}=a_{ji}|Y=c_k)>0,\sum_{l=1}^{S_j}P_\lambda(X^{(j)}=a_{jl}|Y=c_k)=1 \]

通俗的理解就是

\[P(特征a_{jl}|类别c_k)=\frac{类别为c_k的样本中特征为a_{ji}的样本的数量+\lambda}{类别为c_k的样本总数+特征的类别的数量\times \lambda} \]

这个做法和上面是一样的。也就是在类别\(c_k\)下对于每个特征\(a_{il}\)都赋予了一个正数\(\lambda>0\).​​

后面的说明，就是通过这种变换能够使得概率都大于0，并且求和仍然为1，即没有改变概率和为1的基本要求。

我们注意到，当\(\lambda=0\)就是上面的极大似然估计。

我们通常取\(\lambda=1\)，这时候被称为拉普拉斯平滑(Laplacian smoothi

示例 以李航统计学习方法P63 例4.1下的表4.1为例，来确定\(x=(2,S)^T\)的标签\(y\)

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
\(X^{(1)}\)	1	1	1	1	1	2	2	2	2	2	3	3	3	3	3
\(X^{(2)}\)	S	M	M	S	S	S	M	M	L	L	L	M	M	L	L
\(Y\)	-1	-1	1	1	-1	-1	-1	1	1	1	1	1	1	1	-1

1 极大似然估计法

我们有

\[P(Y=-1)=\frac{9}{15} \ \ P(Y=1)=\frac{6}{15} \]

我们可以计算出条件概率

\[\begin{aligned} &P(X^{(1)}=1|Y=1)=\frac{2}{9} , P(X^{(1)}=2|Y=1)=\frac{3}{9} , P(X^{(1)}|Y=1)=\frac{4}{9} \\ &P(X^{(2)}=S|Y=1)=\frac{1}{9} ,P(X^{(2)}=M|Y=1)=\frac{4}{9} , P(X^{(2)}=L|Y=1)=\frac{4}{9} \\ &P(X^{(1)}=1|Y=-1)=\frac{3}{6} , P(X^{(1)}=2|Y=-1)=\frac{2}{6} , P(X^{(1)}|Y=-1)=\frac{1}{6} \\ &P(X^{(2)}=S|Y=-1)=\frac{3}{6} , P(X^{(2)}=M|Y=-1)=\frac{2}{6} , P(X^{(2)}=L|Y=-1)=\frac{1}{6} \\ \end{aligned} \]

对于给定的样本\(x=(2,S)^T\) 计算：

\[P(Y=1) P(X^{(1)}=2|Y=1)P(X^{(2)}=S|Y=1)=\frac{9}{15} \cdot \frac{3}{9} \cdot \frac{1}{9}= \frac{1}{45} \\ P(Y=-1) P(X^{(1)}=2|Y=-1)P(X^{(2)}=S|Y=-1)=\frac{6}{15} \cdot \frac{2}{6} \cdot \frac{3}{6}= \frac{1}{15} \]

因为在第二个类别\(Y=-1\)下，后验概率更大，所以样本\(x=(2,S)^T\)​的标签应该为\(-1\)

2 贝叶斯估计法

取\(\lambda=1\)

我们有

\[P_{\lambda}(Y=-1)=\frac{10}{17} \ \ P_{\lambda}(Y=1)=\frac{7}{17} \]

我们可以计算出条件概率

\[\begin{aligned} &P_{\lambda}(X^{(1)}=1|Y=1)=\frac{3}{12} , P(X^{(1)}=2|Y=1)_{\lambda}=\frac{4}{12} , P_{\lambda}(X^{(1)}|Y=1)=\frac{5}{12} \\ &P_{\lambda}(X^{(2)}=S|Y=1)=\frac{2}{12} ,P_{\lambda}(X^{(2)}=M|Y=1)=\frac{5}{12} , P_{\lambda}(X^{(2)}=L|Y=1)=\frac{5}{12} \\ &P_{\lambda}(X^{(1)}=1|Y=-1)=\frac{3}{6} , P(X^{(1)}_{\lambda}=2|Y=-1)=\frac{2}{6} , P(X^{(1)}|Y=-1)=\frac{1}{6} \\ &P(X^{(2)}=S|Y=-1)=\frac{3}{6} , P(X^{(2)}=M|Y=-1)=\frac{2}{6} , P(X^{(2)}=L|Y=-1)=\frac{1}{6} \\ \end{aligned} \]

对于给定的样本\(x=(2,S)^T\) 计算：

\[P(Y=1) P(X^{(1)}=2|Y=1)P(X^{(2)}=S|Y=1)=\frac{9}{15} \cdot \frac{3}{9} \cdot \frac{1}{9}= \frac{1}{45} \\ P(Y=-1) P(X^{(1)}=2|Y=-1)P(X^{(2)}=S|Y=-1)=\frac{6}{15} \cdot \frac{2}{6} \cdot \frac{3}{6}= \frac{1}{15} \]

因为在第二个类别\(Y=-1\)下，后验概率更大，所以样本\(x=(2,S)^T\)​的标签应该为\(-1\)

优缺点

朴素贝叶斯的主要优点有：

1）朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。

2）对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练。

3）对缺失数据不太敏感，算法也比较简单，常用于文本分类。

朴素贝叶斯的主要缺点有：

1） 理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。

2）需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。

3）由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。

4）对输入数据的表达形式很敏感。

常用模型

伯努利朴素贝叶斯

（3）如果特征是离散性数据并且值只有0和1两种情况，推荐使用伯努利模型。在伯努利模型中，每个特征的取值是布尔型的，即True和False，或者1和0。在文本分类中，表示一个特征有没有在一个文档中出现

代码实现

from sklearn.naive_bayes import BernoulliNB

多项式朴素贝叶斯

使用情形

（1）如果特征是离散型数据，比如文本这些，推荐使用多项式模型来实现。该模型常用于文本分类，特别是单词，统计单词出现的次数

代码实现

#导入朴素贝叶斯——多项式方法
from sklearn.naive_bayes import MultinomialNB
multi_nb = MultinomialNB()
#进行训练
multi_nb.fit(x_train,y_train)
#评分法计算准确率
multi_accracy = multi_nb.score(x_test,y_test)
#预测
multi_nb_pred_result =  multi_nb.predict(data_predict)

高斯朴素贝叶斯

（2）如果特征是连续型数据，比如具体的数字，推荐使用高斯模型来实现，高斯模型即正态分布。当特征是连续变量的时候，运用多项式模型就会导致很多误差，此时即使做平滑，所得到的条件概率也难以描述真实情况。所以处理连续的特征变量，应该采用高斯模型

代码实现

#（4）高斯模型训练
# 导入朴素贝叶斯--高斯模型方法
from sklearn.naive_bayes import GaussianNB
# gauss_nb接收高斯方法
gauss_nb = GaussianNB()
# 模型训练，输入训练集
gauss_nb.fit(x_train,y_train)
# 计算准确率--评分法
gauss_accuracy = gauss_nb.score(x_test,y_test)
# 预测
gauss_result = gauss_nb.predict(data_predict_feature)