支持向量机 SVM
支持向量机 SVM
算法思想概述
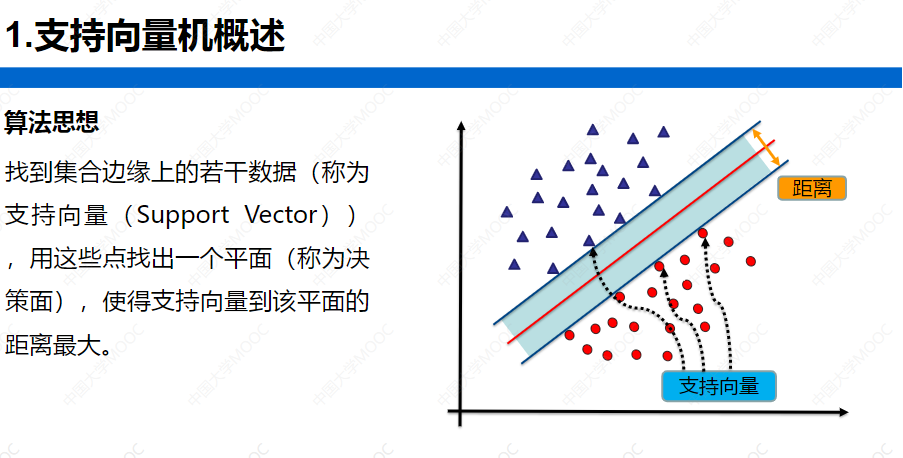
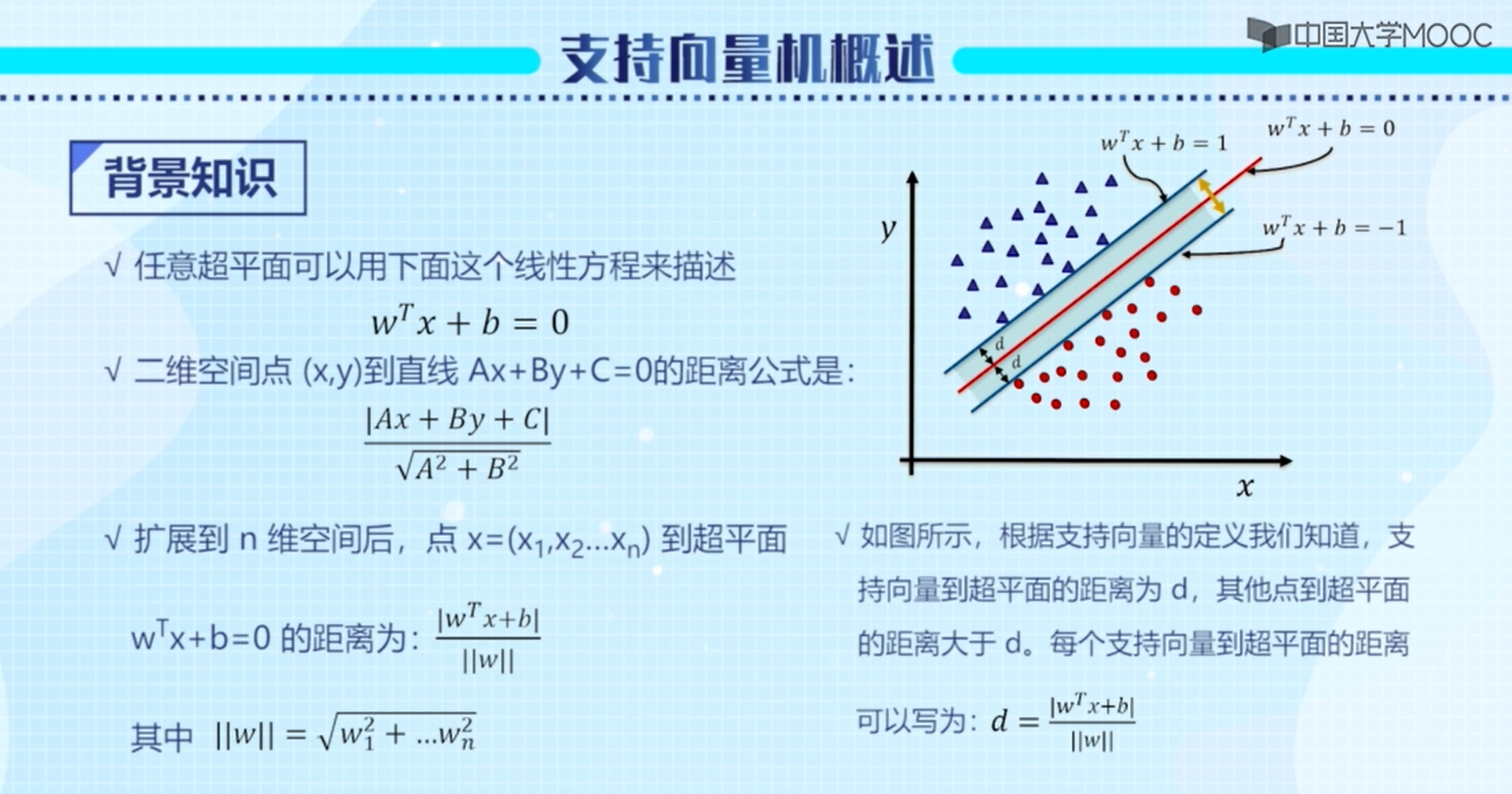
背景知识
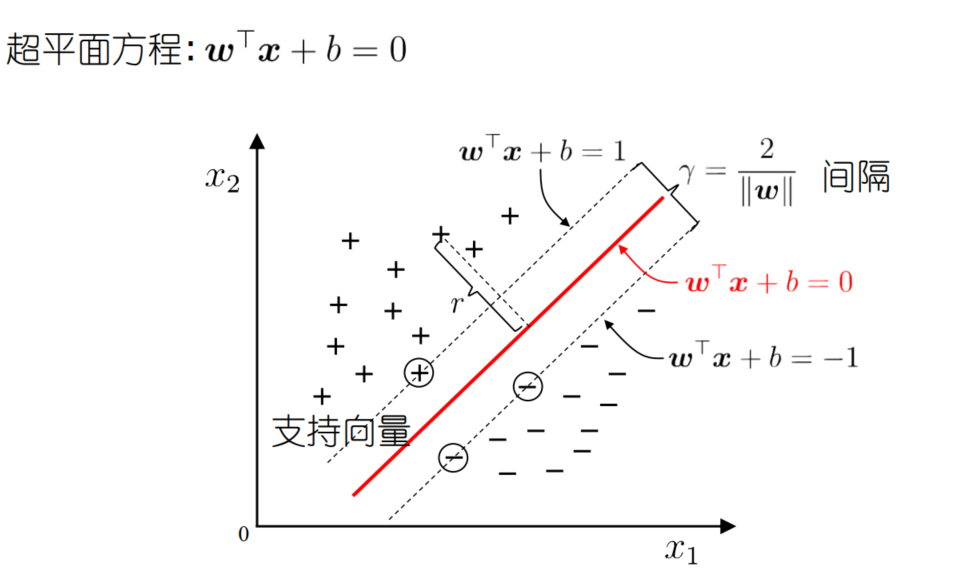
间隔最大化
间隔
定义 7.2

求解最大间隔
方法1 转化为凸函数求解

算法7.1
输入: 线性可分训练数据集 \(T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}\),其中\(x_i \in \mathcal{X}=R^n;y_i \in \mathcal{Y}=\{-1,+1\},i=1,2,\cdots,N;\)
输出:最大间隔分离超平面和分类决策函数
算法:
- 构造并求解约束最优化问题:
\[\begin{aligned} \underset{w,b}{min} & \frac{1}{2} ||w||^2 \\ s.t. &y_i(w\cdot x_i +b)-1 \geq 0 , i=1,2,\cdots,N \end{aligned} \]偏导=0,求得最优解\(w^* ,b^*\)
- 由此得到
分离超平面:$w^* \cdot x+ b^* =0 $
分类决策函数: \(f(x)=sign(w^* \cdot x +b^*)\)
算例
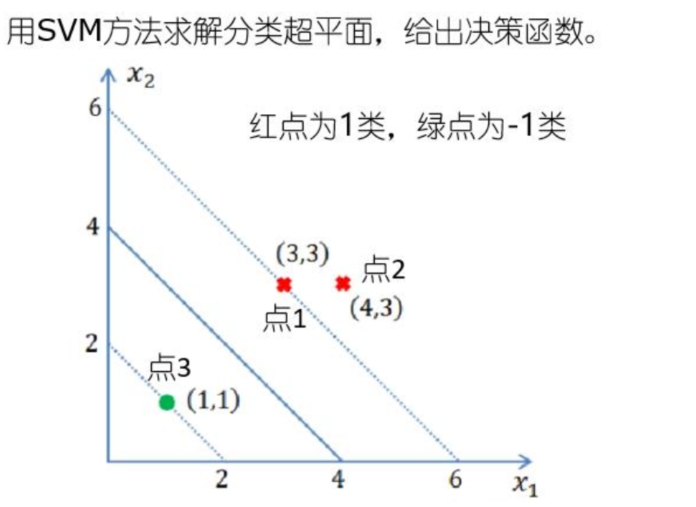
解:由图可知,正例点为\(x_1=(3,3)^T,x_2=(4,3)^T\)负例点为\(x_3=(1,1)^T\)
- 构造约束最优化问题
\[\begin{aligned} \underset{w,b}{min} \ \ & \frac{1}{2} (w_1^2+w_2^2) \\ s.t. \ \ &1(w_1\cdot 3+w_2\cdot 3 +b) \geq 1 \\ &1(w_1\cdot 4+w_2\cdot 3 +b) \geq 1 \\ &-1(w_1\cdot 1+w_2\cdot 1 +b) \geq 1 \\ \end{aligned} \]
求解,得到最优化问题的解\(w_1=w_2=\frac{1}{2},b=-2\)
于是得到分离超平面:$\frac{1}{2}x1+\frac{1}{2}x2 -2 =0 $ ,其中\(x_1=(3,3),x_3=(1,1)\)是支持向量
分类决策函数: \(f(x)=sign(\frac{1}{2}x^1+\frac{1}{2}x^2 -2)\)
方法2 求解对偶问题 (拉格朗日乘子法和KKT条件)
优点
- 对偶问题更容易求解
- 可以引入核函数
推导
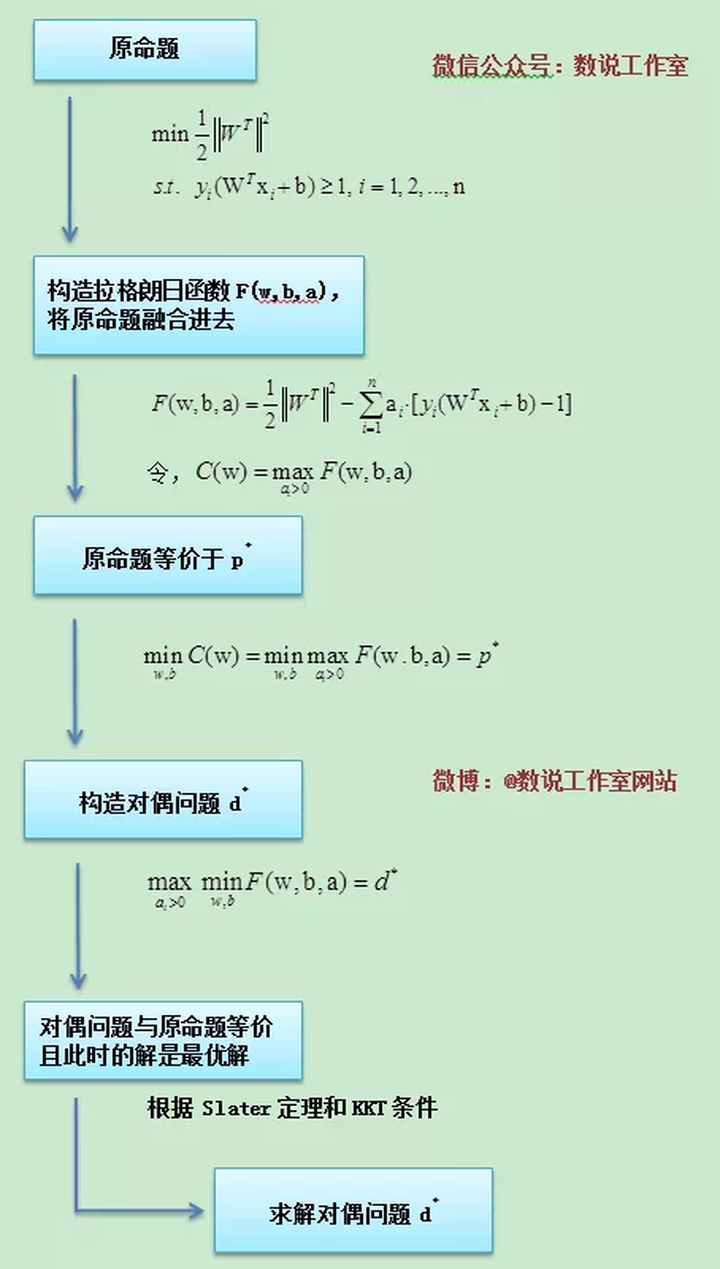
算法7.2
输入: 线性可分训练数据集 \(T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}\),其中\(x_i \in \mathcal{X}=R^n;y_i \in \mathcal{Y}=\{-1,+1\},i=1,2,\cdots,N;\)
输出:最大间隔分离超平面和分类决策函数
算法:
- 构造并求解约束最优化问题:
\[\begin{aligned} \underset{a}{min} & \frac{1}{2} \sum_{i=1}^N\sum_{j=1}^N a_ia_j y_iy_j(x_i \cdot x_j)-\sum_{i=1}^Na_i\\ s.t. &\sum_{i=1}^N a_iy_i=0 \\ &a_i \geq 0, \ \ i=1,2,\cdots,N \end{aligned} \]这个计算过程就是令偏导=0来求解,求得最优解\(a^*=(a_1^*,a_2^*,\cdots a_N^*)\)
- 计算 \(w^* = \sum_{i=1}^N a_i^*y_ix_i\)
选择\(a^*\)的一个正分量\(a_j^*>0\),计算\(b^* = y_j - \sum_{i=1}^N a_i^*y_i(x_i \cdot x_j)\)
- 由此得到
分离超平面:$w^* \cdot x+ b^* =0 $
分类决策函数: \(f(x)=sign(w^* \cdot x +b^*)\)
在线性可分向量机中,\(w^*,b^*\)只依赖于数据中对应\(a_i^* >0\)的样本点\((x_i,y_i)\).而其他样本点对\(w^*,b^*\)没有影响。我们将对应于对应\(a_i^* >0\)的样本点称为支持向量
算例

解:由图可知,正例点为\(x_1=(3,3)^T,x_2=(4,3)^T\)负例点为\(x_3=(1,1)^T\) ,有三个点所以有三个拉格朗日乘子\(a_1,a_2,a_3\)
- 写出对偶问题
\[\begin{aligned} \underset{a}{min} & \frac{1}{2} \sum_{i=1}^N\sum_{j=1}^N a_ia_j y_iy_j(x_i \cdot x_j)-\sum_{i=1}^Na_i\\ &= \frac{1}{2}(18a_1^2+25a_2^2+2a_3^2+42a_1a_2-12a_1a_3-14a_2a_3)-(a_1+a_2+a_3) \\ s.t. & a_1+a_2-a_3=0 \\ &a_i \geq 0, \ \ i=1,2,\cdots,N \end{aligned} \]
- 求解 。
将\(a_3=a_1+a_2\)带入目标函数并记为\(s(a_1,a_2)=4a_1^2+\frac{13}{2}a_2^2+10a_1a_2-2a_1-2a_2\)
对\(a_1,a_2\)求偏导令其为0
\[\{ \begin{array}{rcl} &8a_1+10a_2-2 =0 \\ &13a_2+10a_1-2 =0 \end{array} \ \ \ \ \{ \begin{array}{rcl} a_1 & =\frac{3}{2} \\ a_2 &=-1 \end{array} \]得知,\(s(a_1,a_2)\)在点\((\frac{3}{2},-1)\)取极值。但该点不满足约束条件\(a_2>0\),所以最小值应该在边界上达到
- 当\(a_1=0\) ,\(s(a_1,a_2)=\frac{13}{2}a_2^2-2a_2\),最小值\(s(0,\frac{2}{13})=-\frac{2}{13}\)
- 当\(a_2=0\) ,\(s(a_1,a_2)=4a_1^2-2a_1\),最小值\(s(\frac{1}{4},0)=-\frac{1}{4}\)
所以\(s(a_1,a_2)\)在\(a_1=\frac{1}{4},a_2=0\)达到最小,此时\(a_3=a_1+a_2=\frac{1}{4}\)
- 这样,\(a_1^* = a_3^* = \frac{1}{4}\)对应的实例点\(x_1,x_3\)是支持向量。
\(w^* = \frac{1}{4}\cdot1 \cdot(3,3)+\frac{1}{4}\cdot -1 \cdot(1,1)=(\frac{1}{2},\frac{1}{2})\)
选择实例点\((1,1),-1\), \(a=\frac{1}{4}\),计算\(b^*= -1- [\frac{1}{4}\cdot -1 \cdot(3 \cdot1)+\frac{1}{4}\cdot -1 \cdot(1 \cdot 1)]=-2\)
- 于是得到分离超平面:$\frac{1}{2}x1+\frac{1}{2}x2 -2 =0 $ ,其中\(x_1=(3,3),x_3=(1,1)\)是支持向量
分类决策函数: \(f(x)=sign(\frac{1}{2}x^1+\frac{1}{2}x^2 -2)\)
软间隔
训练数据中有一些样本点不能满足函数间隔大于等于1的约束条件,为了解决这个问题,可以对每个样本点引入一个松弛变量\(\xi_i \geq 0\) ,使得函数间隔加上松弛变量大于等于1.这样,约束条件变为
同时,对每一个松弛变量\(\xi_i\),支付一个代价\(\xi_i\)。目标函数由原来的\(\frac{1}{2}||w||^2\)变成
这里,\(C\)称为惩罚参数,一般由应用问题决定,\(C\)值大时对误分类的惩罚增大,\(C\)值小时对误分类的惩罚减小。
此时问题就变成如下凸二次规划问题(原始问题):
对应的对偶问题是
算法7.3
输入: 线性可分训练数据集 \(T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}\),其中\(x_i \in \mathcal{X}=R^n;y_i \in \mathcal{Y}=\{-1,+1\},i=1,2,\cdots,N;\)
输出:分离超平面和分类决策函数
算法:
- 选择惩罚函数\(C>0\),构造并求解凸二次规划问题:
\[\begin{aligned} \underset{a}{min} &\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N a_ia_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^Na_i \\ s.t. &\sum_{i=1}^N a_iy_i =0 \\ & 0 \leq a_i \leq C ,i=1,2,\cdots,N \end{aligned} \]这个计算过程就是令偏导=0来求解,求得最优解\(a^*=(a_1^*,a_2^*,\cdots a_N^*)\)
- 计算 \(w^* = \sum_{i=1}^N a_i^*y_ix_i\)
选择\(a^*\)的一个正分量$ 0 <a_j*<C$,计算$b* = y_j - \sum_{i=1}^N a_i^*y_i(x_i \cdot x_j)$
- 由此得到
分离超平面:$w^* \cdot x+ b^* =0 $
分类决策函数: \(f(x)=sign(w^* \cdot x +b^*)\)
在线性可分向量机中,\(w^*,b^*\)只依赖于数据中对应\(a_i^* >0\)的样本点\((x_i,y_i)\).而其他样本点对\(w^*,b^*\)没有影响。我们将对应于对应\(a_i^* >0\)的样本点称为支持向量
核技巧
用线性分类方法求解非线性分类问题分为两步:
- 首先使用一个变换将原空间的数据映射到新空间中
- 然后在新空间用线性分类学习方法从训练数据中学习分类模型。
核技巧就属于这样的方法。
核技巧应用到支持向量机,其基本想法就是通过一个非线性变换将输入空间(欧式空间\(R^n\)或者离散集合)对应一个特征空间(希尔伯特空间\(\mathcal{H}\)),是的输入空间\(R^n\)中的超平面模型对应于特征空间\(\mathcal{H}\)中的超平面模型(支持向量机)。这样分类问题的学习任务通过在特征空间中求解线性支持向量机就可以完成。
核函数
定义7.6 (核函数)
设\(\mathcal{X}\)是输入空间(欧式空间\(R^n\)或者离散集合),又设\(\mathcal{H}\)为特征空间(希尔伯特空间\(\mathcal{H}\)),如果存在一个从\(\mathcal{X}\)到\(\mathcal{H}\)的映射
\[\phi(x): \mathcal{X} \rightarrow \mathcal{H} \]使得对所有\(x,z\in \mathcal{X}\),函数\(K(x,z)\)满足条件
\[K(x,z) = \phi(x) \cdot \phi(z) \]则称\(K(x,z)\)为核函数,\(\phi(x)\)为映射函数,式中\(\phi(x) \cdot \phi(z)\)为\(\phi(x)\)和\(\phi(z)\)的内积
核技巧的想法是,在学习和预测中只定义核函数\(K(x,z)\),而不显式地定义映射函数\(\phi\).通常,直接计算\(K(x,z)\)比较容易,而通过映射$$
我们注意到在线性支持向量机的对偶问题中,无论是目标函数还是决策函数(分离超平面)都只涉及输入实例与实例之间的内积。在对偶问题的目标函数中的内积\(x \cdot y\)可以用核函数\(K(x_i,x_j)=\phi(x_i)\cdot \phi(x_j)\)来替代。此时对偶问题的目标函数成为
同样分类决策函数中的内积也可以用核函数替代,而分类决策函数式成为
这等价于经过映射函数\(\phi\)将原来的输入空间变换到一个新的特征空间,将输入空间中的内积\(x_i \cdot x_j\)变换为特征空间中的内积\(\phi(x_i)\cdot\phi(x)\),在新的特征空间里从训练样本呢中学习线性支持向量机。
常用的核函数
- 多项式核函数
对应的支持向量机是一个\(p\)次多项式分类器。在此情形下,分类决策函数变为
-
高斯核函数
\[K(x,z) = exp(-\frac{||x-z||^2}{2 \sigma^2}) \]对应的支持向量机是一个高斯径向基函数分类器。在此情形下,分类决策函数变为
\[f(x)=sign(\sum_{i=1}^{N_s}a_i^*y_i exp(-\frac{||x-x_i||^2}{2 \sigma^2})+b^*) \] -
字符串核函数
算法7.4
输入: 线性可分训练数据集 \(T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}\),其中\(x_i \in \mathcal{X}=R^n;y_i \in \mathcal{Y}=\{-1,+1\},i=1,2,\cdots,N;\)
输出:分离超平面和分类决策函数
算法:
- 选择适当的核函数\(K(x,z)\)和惩罚函数\(C>0\),构造并求解最优化问题:
\[\begin{aligned} \underset{a}{min} &\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N a_ia_jy_iy_jK(x_i \cdot x_j) - \sum_{i=1}^Na_i \\ s.t. &\sum_{i=1}^N a_iy_i =0 \\ & 0 \leq a_i \leq C ,i=1,2,\cdots,N \end{aligned} \]这个计算过程就是令偏导=0来求解,求得最优解\(a^*=(a_1^*,a_2^*,\cdots a_N^*)\)
- 计算 \(w^* = \sum_{i=1}^N a_i^*y_ix_i\)
选择\(a^*\)的一个正分量$ 0 <a_j*<C$,计算$b* = y_j - \sum_{i=1}^N a_i^*y_i(x_i \cdot x_j)$
- 由此得到
分离超平面:$w^* \cdot x+ b^* =0 $
分类决策函数: \(f(x)=sign(\sum_{i=1}^{N_s}a_i^*y_i K(x_i,x)+b^*)\)
在线性可分向量机中,\(w^*,b^*\)只依赖于数据中对应\(a_i^* >0\)的样本点\((x_i,y_i)\).而其他样本点对\(w^*,b^*\)没有影响。我们将对应于对应\(a_i^* >0\)的样本点称为支持向量
SMO算法
支持向量机的学习问题可以形式化为求解二次规划问题。这样的凸二次规划问题具有全局最优解,并且由许多最优化算法可以用来求解,但是当训练样本容量很大时,这些算法往往变得低效。序列最小最优化(sequential minimal optimization ,SMO)
SMO算法要求解如下凸二次规划的对偶问题:
在这个问题中,变量是拉格朗日橙子,一个变量\(a_i\)对应一个样本点\((x_i,y_i)\);变量的总数等于训练样本容量\(N\)
SMO算法是一种启发式算法,基本思想是:如果所有变量的解都满足最优化问题的KKT条件,那么这个最优化问题的解就得到了。否则,选择两个变量,固定其他变量,针对这两个变量构建一个二次规划问题。子问题有两个变量,一个是违反KKT条件最严重的那一个,另一个由约束条件自动确定。SMO算法将原问题不断分解为子问题并对子问题求解,从而达到求解原问题的目的。
不失一般性,假设选择的两个变量是\(a_1,a_2\),其他变量\(a_i(i=3,4,\cdots,N)\)是固定的。于是SMO的最优化问题的子问题可以写成:
其中,\(K_{ij}=K(x_i,x_j),i,j=1,2,\cdots,N\),\(\varsigma\)是常数,目标函数式中省略了不含\(a_1,a_2\)的常数项
算法 7.5 SMO
输入: 线性可分训练数据集 \(T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}\),其中\(x_i \in \mathcal{X}=R^n;y_i \in \mathcal{Y}=\{-1,+1\},i=1,2,\cdots,N;\) 精度\(\epsilon\)
输出:近似解\(\hat{a}\)
算法:
1取初始值\(a^{(0)}=0\),令\(k=0\)
2选取优化变量\(a_1^{(k)},a_2^{(k)}\),解析求解两个变量的最优化问题
\[\begin{aligned} \underset{a_1,a_2}{min} \ W(a_1,a_2)= &\frac{1}{2}K_{11}a_1^2+ \frac{1}{2}K_{22}a_2^2+y_1y_2K_{12}a_1a_2-(a_1+a_2)\\ &+y_1a_1\sum_{i=3}^Ny_ia_iK_{i1}+y_2a_2\sum_{i=3}^Ny_ia_iK_{i2}\\ s.t. & a_1y_1 +a_2y_2=-\sum_{i=3}^Ny_ia_i=\varsigma \\ & 0 \leq a_i \leq C ,i=1,2 \end{aligned} \]求得最优解\(a_1^{(k+1)},a_2^{(k+1)}\),更新\(a\)为\(a^{(k+1)}\)
- 3若在精度\(\epsilon\)范围内满足停止条件
\[\sum_{i=1}^N a_iy_i = 0 ,&0\leq a_i \leq C , i=1,2,\cdots,N \\ y_i \cdot g(x_i) & \left\{ \begin{array}{rcl} \geq 1 , & \{ x_i| a_i=0\}\\ =1 , & \{ x_i|0< a_i <C\} \\ \leq 1, & \{ x_i| a_i=C\} \end{array}\right. \\ \text{其中} \\ g(x_i)& = \sum_{j=1}^N a_jy_jK(x_j,x_i)+b \]则转到(4);否则令\(k=k+1\),传到(2)
- 4 取 \(\hat{a} = a^{(k+1)}\)
感谢
参考 李航 统计学习方法
本文来自博客园,作者:{珇逖},转载请注明原文链接:https://www.cnblogs.com/zuti666/p/15582615.html

