线性回归

线性回归

目录

• 线性回归
  • 符号约定 ：
  • 算法流程
  • 理解
  • 求解
    • 方法一 标准方程法
    • 方法二 梯度下降法
      • 批量梯度下降法 BGD （Batch Gradient Descent)
      • 随机梯度下降 SGD Stochastic Gradient Descent
      • 小批量梯度下降 MBGD（Mini-Batch Gradient Descent）
    • 比较
  • 回归的评价指标

---

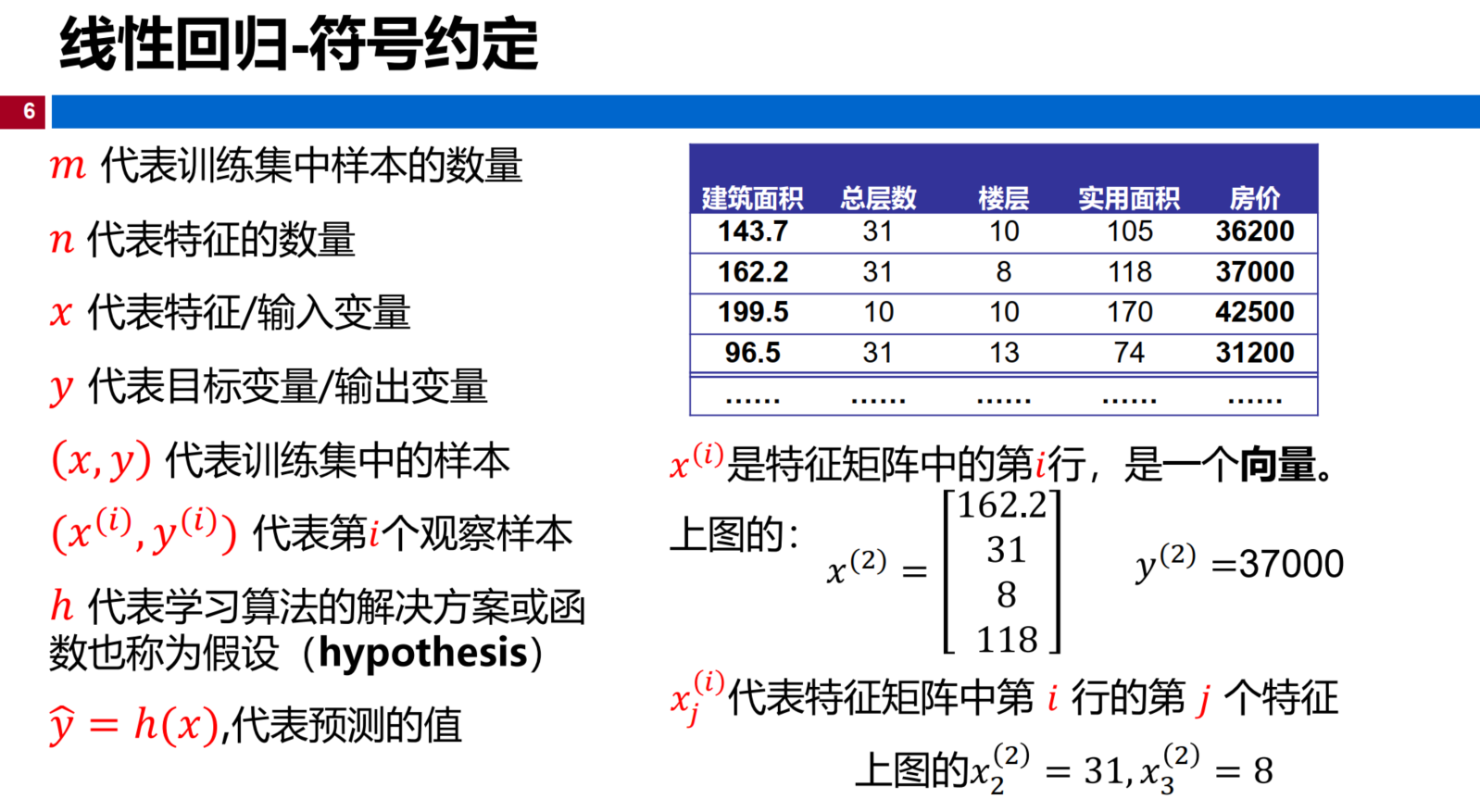
符号约定 ：

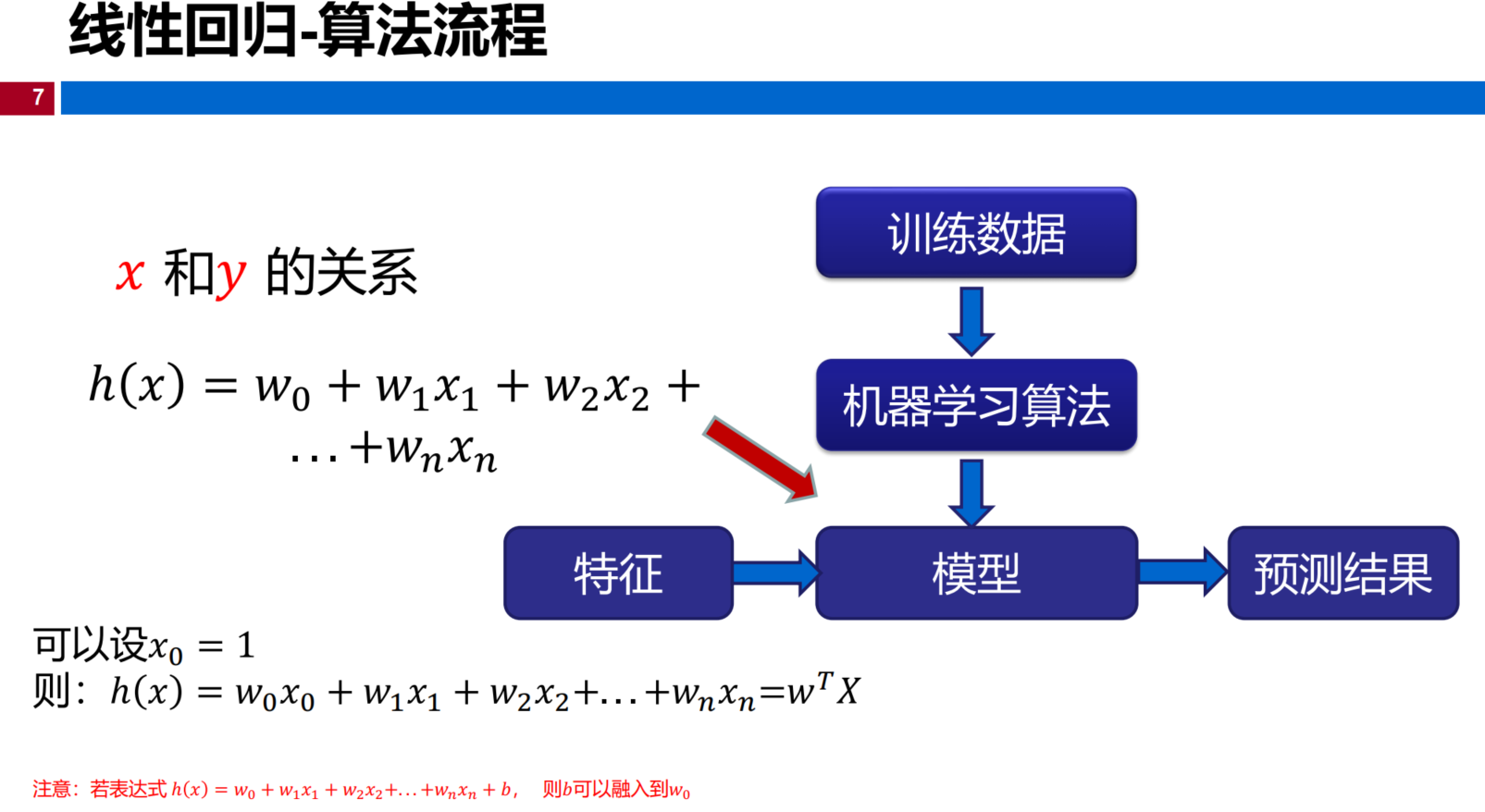
算法流程

理解

使用训练数据来找到线性回归方程中的参数\(w_0,w_1,\dots,w_n\)使得回归方程的预测值和真实值的误差最小。

这个误差可以使用 平方衡量 ，也可以使用 绝对值 等方式衡量。

寻找的过程可以直接解优化方程，也可以使用迭代法不断更新。

求解

• 目标函数 ：\(\hat{y}=h(x)=w_0+w_1x_1+\cdots + w_{n-1}x_{n-1}+w_nx_n=wX\)​

  我们的目的是的值目标函数中的未知参数的值，即\(w_0,w_1,\cdots,x_n\)​

  n表示特征数量​

• 损失函数 ： \(J(w)=\frac{1}{2m} *\sum_{i=1}^m(h(x_i)-y)^2 =\frac{1}{2}(Xw-Y)^2= \frac{1}{2}(Xw-Y)^T(Xw-Y)\)​

  m表示样本数量，也就是所有样本的预测值与真实值之差的平方求和再去平均 ，不过技巧性地加了1/2

  我们将训练集中的样本\((x_1,x_2,\cdots,x_n,y)_1,\cdots,(x_1,x_2,\cdots,x_n,y)_n\)带入到损失函数中，那么损失函数就是关于\(w\)的函数，

  我们目标是使误差最小，也就是\(J(w)\)最小​

方法一 标准方程法

显然损失函数是一个二次函数，在导数为0的时候取得最小值，那我们就求偏导为0，然后求解这个时候的\(w\)​值

\[\begin{aligned} \frac{\partial J(w)}{\partial{w}} &=\frac{1}{2}\frac{\partial }{\partial{w}}(Xw-Y)^T(Xw-Y) \\ &=\frac{1}{2}\frac{\partial }{\partial{w}}(w^TX^TXw-Y^TXw-w^TX^TY+Y^TY) \\ &=\frac{1}{2}(2X^TXw-Y^TX-X^TY+0)\\ &=X^TXw-X^TY \\ 令 \frac{\partial J(w)}{\partial{w}}=0 \\ &X^TXw-X^TY=0 \\ w &= (X^TX)^{-1}X^TY \end{aligned} \]

注释： 矩阵的求导法则，以及矩阵的转置

\[(A^T)^T=A ,(AB)^T=B^TA^T,(kA)^T=kA^T,(A \pm B)^T= A^T \pm B^T \\ \frac{dX^TX}{d X}=2X ,\frac{dAX}{d X}=A^T \\ \frac{\partial X^TAX}{\partial{X}}=(A+A^T)X ,若A为对称矩阵，\frac{\partial X^TAX}{\partial{X}}=2AX \]

需要注意的是，为了求出\(w\)的值，我们需要求逆矩阵，我们知道矩阵的逆并不是一定存在的

矩阵可逆 等价于 矩阵满秩 等价于 矩阵正定

在数学上，当矩阵求不出逆矩阵时，我们可以用伪逆矩阵来代替

矩阵不可逆的情形主要有这几个原因

• 特征值不是相互独立的，是线性相关的

• 特征数太多

  对于这几种情形，我们可以采用特征缩放（降维），数据归一化等进行处理

方法二 梯度下降法

梯度下降公式

\[w_j := w_j -\alpha \frac{\partial J(w)}{\partial{w_j}} \]

注意这里的

• \(\alpha\)表示 学习率 ，也就是前进的步长
• \(\frac{\partial J(w)}{\partial{w_j}}\)表示梯度方向，梯度方向前面加负号 表示是梯度下降方向
• 更新是对于\(w_j\)的
• 迭代的时候会存在陷入局部最小值和步长选取不恰当的问题

根据每次迭代使用的数据情况，我们将梯度下降分为

1. 批量梯度下降 BGD （Batch Gradient Descent)

   梯度下降的每一步，使用所有的训练样本

2. 随机梯度下降 SGD （Stochastic Gradient Descent）

   梯度下降的每一步，用到一个样本

3. 小批量梯度下降 MBGD（Mini-Batch Gradient Descent）

   梯度下降的每一步，用到了一定批量的训练样本

批量梯度下降法 BGD （Batch Gradient Descent)

梯度下降的每一步，使用所有的训练样本

\[\begin{aligned} w_j : &= w_j -\alpha \frac{1}{m}\sum_{i=1}^m( \frac{\partial J(w)}{\partial{w_j}}) \\ &= w_j -\alpha \frac{1}{m}\sum_{i=1}^m( \ (h(x^{(i)})-y^{(i)}) \cdot x^{(i)}_j \ ) \end{aligned} \]

上标 \(i\) 表示在计算时使用的第\(i\)​个样本

随机梯度下降 SGD Stochastic Gradient Descent

梯度下降的每一步，用到一个样本，在每一次计算之后便更新参数，而不
需要首先将所有的训练集求和

\[\begin{aligned} w_j : &= w_j -\alpha \frac{\partial J(w)}{\partial{w_j}} \\ &= w_j -\alpha \ (h(x^{(i)})-y^{(i)}) \cdot x^{(i)}_j \ \end{aligned} \]

同步更新 \(w_j,(j=0,1,\cdots,n)\)

推导：

\[\begin{aligned} w & = w - \alpha \frac{\partial J(w)}{\partial{w}} \\ h(x) &= w^TX=w_0x_0+w_1x_1+\cdots + w_{n-1}x_{n-1}+w_nx_n =\sum_{i=0}^n w_ix_i\\ J(w) &= \frac{1}{2} *(h(x_i^{(i)})-y^{(i)})^2 \\ \frac{\partial J(w)}{\partial{w_j}} &= \frac{\partial }{\partial{w_j}}\frac{1}{2} (h(x_i^{(i)})-y^{(i)})^2 \\ &=2 \cdot \frac{1}{2} (h(x_i^{(i)})-y^{(i)}) \cdot \frac{\partial }{\partial{w_j}} (h(x_i^{(i)})-y^{(i)}) \\ &= (h(x_i^{(i)})-y^{(i)}) \cdot \frac{\partial }{\partial{w_j}} (\sum_{i=0}^nw_ix_i^{(i)}-y^{(i)}) \\ &= (h(x_i^{(i)})-y^{(i)})x_j^{(i)} \end{aligned} \]

小批量梯度下降 MBGD（Mini-Batch Gradient Descent）

梯度下降的每一步中，用到了一定批量的训练样本。每计算常数𝑏次训练实例，便更新一次参数 𝑤

\[\begin{aligned} w_j : &= w_j -\alpha \frac{1}{b}\sum_{k=i}^{i+b-1}( \frac{\partial J(w)}{\partial{w_j}}) \\ &= w_j -\alpha \frac{1}{b}\sum_{k=i}^{i+b-1}( \ (h(x^{(k)})-y^{(k)}) \cdot x^{(k)}_j \ ) \end{aligned} \]

同步更新 \(w_j,(j=0,1,\cdots,n)\)

• b=1 随机梯度下降,SGD
• b=m 批量梯度下降,BGD
• b=batch_size 通常是2的指数倍，常见有32,64,128等 小批量梯度下降,MBGD

比较

梯度下降法	标准方程法（最小二乘法）
需要选择学习率，需要多次迭代	一次计算得出，需要计算逆矩阵
当特征数量大的时候也能使用，适合各类模型	当特征数量较大时运算代价大，只适用于线性模型

回归的评价指标