决策树 机器学习，西瓜书p80 表4.2 使用信息增益生成决策树及后剪枝

使用信息增益构造决策树，完成后剪枝

目录

1 构造决策树

1 根结点的选择

色泽 信息增益

根据色泽划分为 青绿，乌黑，浅白 三个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\ Ent(D^2) &= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\ Ent(D^3)&= -(\frac{2}{2} log_2 \frac{2}{2}+\frac{0}{2} log_2 \frac{0}{2})=0 \\ Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\ Gani(D,色泽)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 1 - (\frac{4}{10}\times 1+\frac{4}{10} \times 0.811+\frac{2}{10}\times0) \\ &= 0.2756 \end{aligned} \]

根蒂 信息增益

根据根蒂划分为 蜷缩 稍蜷 硬挺 三个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{2}{5} log_2 \frac{2}{5}+\frac{3}{5} log_2 \frac{3}{5})=0.971 \\ Ent(D^2) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\ Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\ Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\ Gani(D,根蒂)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 1 - (\frac{5}{10}\times 0.971+\frac{4}{10} \times 1+\frac{1}{10}\times0) \\ &= 0.1145 \end{aligned} \]

敲声 信息增益

根据色泽划分为 浊响，沉闷，清脆 三个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{2}{6} log_2 \frac{2}{6}+\frac{4}{6} log_2 \frac{4}{6})=0.918 \\ Ent(D^2) &= -(\frac{2}{3} log_2 \frac{2}{3}+\frac{1}{3} log_2 \frac{1}{3})=0.918 \\ Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\ Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\ Gani(D,敲声)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 1 - (\frac{6}{10}\times 0.918+\frac{3}{10} \times 0.918+\frac{1}{10}\times0) \\ &=0.2346 \end{aligned} \]

纹理 信息增益

根据 纹理 划分为 清晰 稍糊 模糊 三个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{2}{6} log_2 \frac{2}{6}+\frac{4}{6} log_2 \frac{4}{6})=0.918 \\ Ent(D^2) &= -(\frac{2}{3} log_2 \frac{2}{3}+\frac{1}{3} log_2 \frac{1}{3})=0.918 \\ Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\ Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\ Gani(D,纹理)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 1 - (\frac{6}{10}\times 0.918+\frac{3}{10} \times 0.918+\frac{1}{10}\times0) \\ &= 0.2346 \end{aligned} \]

脐部 信息增益

根据色泽划分为 凹陷，稍凹，平坦 三个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\ Ent(D^2) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\ Ent(D^3)&= -(\frac{2}{2} log_2 \frac{2}{2}+\frac{0}{2} log_2 \frac{0}{2})=0 \\ Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\ Gani(D,脐部)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 1 - (\frac{4}{10}\times 0.811+\frac{4}{10} \times 1+\frac{2}{10}\times0) \\ &= 0.2756 \end{aligned} \]

触感 信息增益

根据色泽划分为 硬滑，软粘 两个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{3}{6} log_2 \frac{3}{6}+\frac{3}{6} log_2 \frac{3}{6})=1 \\ Ent(D^2) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\ Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\ Gani(D,触感)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 1 - (\frac{6}{10}\times 1 +\frac{4}{10} \times 1 \\ &= 0 \end{aligned} \]

选择根结点构建决策树

\[\begin{aligned} Gain(D,色泽)=0.2756 \ Gain(D,根蒂)=0.1145 \ Gain(D,敲声)=0.2346 \\ Gain(D,纹理)=0.2346 \ Gain(D,脐部)=0.2756 \ Gain(D,触感)=0 \end{aligned} \]

比较六个属性的信息增益大小，选择脐部作为根结点

则数据集被划分为

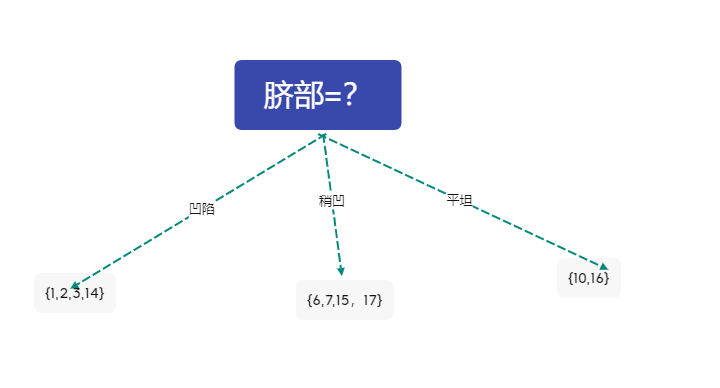
image-20211031203958969

2 对分支结点\({1,2,3,14}\)进行划分

色泽 信息增益

根据色泽划分为 青绿，乌黑，浅白 三个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0 \\ Ent(D^2) &= -(\frac{0}{2} log_2 \frac{0}{2}+\frac{2}{2} log_2 \frac{2}{2})=0 \\ Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\ Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\ Gani(D,色泽)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 0.811 - (\frac{1}{4}\times 0+\frac{2}{4} \times 0 +\frac{1}{4}\times 0) \\ &= 0.811 \end{aligned} \]

根蒂 信息增益

根据根蒂划分为 蜷缩 稍蜷 两个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{0}{3} log_2 \frac{0}{3}+\frac{3}{3} log_2 \frac{3}{3})=0 \\ Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\ Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})= 0.811\\ Gani(D,根蒂)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 0.811 - (\frac{3}{4}\times 0 +\frac{1}{4} \times 0) \\ &= 0.811 \end{aligned} \]

敲声 信息增益

根据色泽划分为 浊响，沉闷 两个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{0}{2} log_2 \frac{0}{2}+\frac{2}{2} log_2 \frac{2}{2})=0 \\ Ent(D^2) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\ Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\ Gani(D,敲声)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 0.811 - (\frac{2}{4}\times 0 +\frac{2}{4} \times 1 ) \\ &=0.311 \end{aligned} \]

纹理 信息增益

根据 纹理 划分为 清晰 稍糊 两个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{0}{3} log_2 \frac{0}{3}+\frac{3}{3} log_2 \frac{3}{3})=0 \\ Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\ Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\ Gani(D,纹理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 0.811 - (\frac{3}{4}\times 0+\frac{1}{4} \times 0 ) \\ &= 0.811 \end{aligned} \]

触感 信息增益

根据触感划分为 硬滑 一个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\ Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})= 0.811 \\ Gani(D,触感)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 0.811 - (\frac{4}{4}\times 0.811 ) \\ &= 0 \end{aligned} \]

选择分类结点构建决策树

\[\begin{aligned} Gain(D,色泽)=0.811 \ Gain(D,根蒂)=0.811 \ Gain(D,敲声)=0.311 \\ Gain(D,纹理)=0.811 \ \ \ Gain(D,触感)=0 \end{aligned} \]

不妨选择色泽作为分类依据

形成的决策树

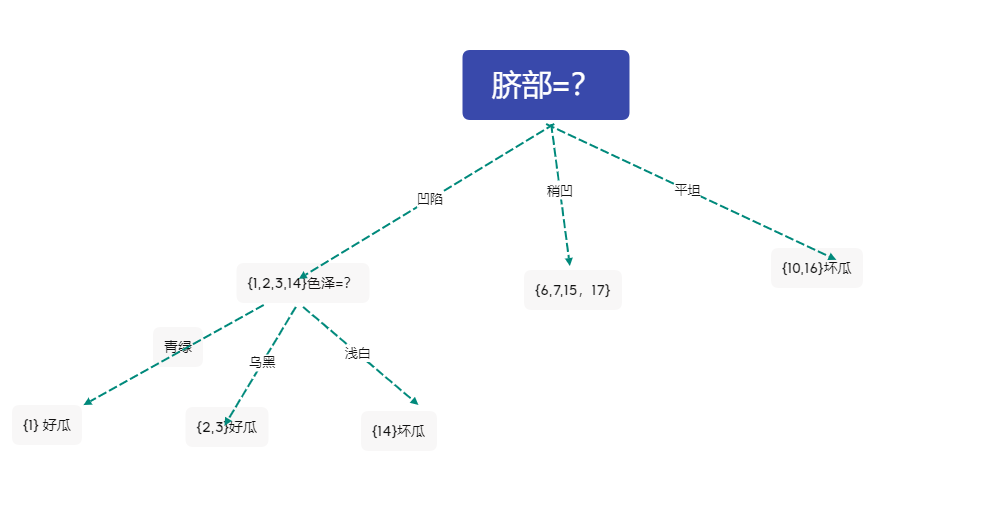
image-20211031211024832

3 对分支 \({6,7,15,17}\)进行划分

色泽 信息增益

根据色泽划分为 青绿，乌黑 两个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\ Ent(D^2) &= -(\frac{1}{2} log_2 \frac{0}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\ Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})= 1 \\ Gani(D,色泽)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 1 - (\frac{2}{4}\times 1+\frac{2}{4} \times 1 ) \\ &= 0 \end{aligned} \]

根蒂 信息增益

根据根蒂划分为 蜷缩 稍蜷 两个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0。918\\ Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\ Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})= 1\\ Gani(D,根蒂)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 1 - (\frac{3}{4}\times 0.918 +\frac{1}{4} \times 0) \\ &= 0.3115 \end{aligned} \]

敲声 信息增益

根据色泽划分为 浊响，沉闷 两个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\ Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})= 0 \\ Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\ Gani(D,敲声)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 1 - (\frac{3}{4}\times 0.918 +\frac{1}{4} \times 0 ) \\ &=0.3115 \end{aligned} \]

纹理 信息增益

根据 纹理 划分为 清晰 稍糊 两个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\ Ent(D^2) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\ Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\ Gani(D,纹理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 1 - (\frac{2}{4}\times 1+\frac{2}{4} \times 1 ) \\ &= 0 \end{aligned} \]

触感 信息增益

根据触感划分为 硬滑，软粘 两个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\ Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\ Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\ Gani(D,触感)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 1 - (\frac{3}{4}\times 0.918+\frac{1}{4} \times 0 ) \\ &= 0.2295 \end{aligned} \]

选择分类结点构建决策树

\[\begin{aligned} Gain(D,色泽)=0 \ Gain(D,根蒂)=0.3115 \ Gain(D,敲声)=0.3115 \\ Gain(D,纹理)=0 \ \ \ Gain(D,触感)=0.2295 \end{aligned} \]

不妨选择根蒂作为分类依据

此时决策树为

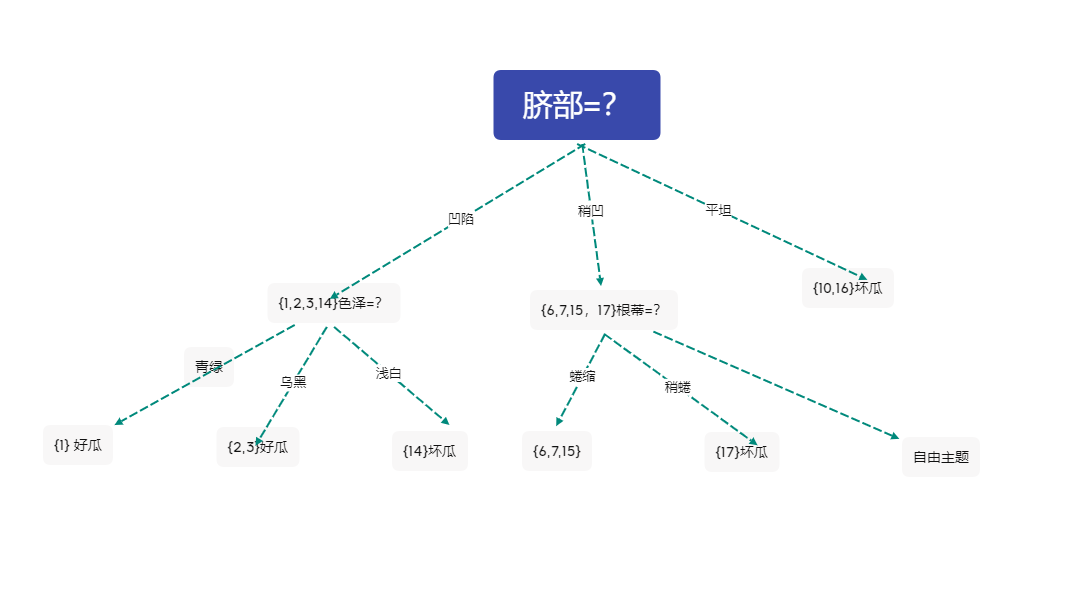
image-20211031213416296

4 对分支\({6,7,15}\)进行划分

色泽 信息增益

根据色泽划分为 青绿，乌黑 两个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0 \\ Ent(D^2) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\ Ent(D)&= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})= 0.918 \\ Gani(D,色泽)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 0.918 - (\frac{1}{3}\times 0+\frac{2}{3} \times 1 ) \\ &= 0.252 \end{aligned} \]

敲声 信息增益

根据色泽划分为 浊响 一个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\ Ent(D)&= -(\frac{2}{3} log_2 \frac{2}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\ Gani(D,敲声)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 0.918 - (\frac{3}{3}\times 0.918 ) \\ &=0 \end{aligned} \]

纹理 信息增益

根据 纹理 划分为 清晰 稍糊 两个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\ Ent(D^2) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0\\ Ent(D)&= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\ Gani(D,纹理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 0.918 - (\frac{2}{3}\times 1+\frac{1}{3} \times 0 ) \\ &= 0.252 \end{aligned} \]

触感 信息增益

根据触感划分为 软粘 一个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\ Ent(D)&= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918\\ Gani(D,触感)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 0.918 - (\frac{3}{3}\times 0.918 ) \\ &= 0 \end{aligned} \]

选择分类结点构建决策树

\[\begin{aligned} Gain(D,色泽)=0 .252 \ \ Gain(D,敲声)=0 \\ Gain(D,纹理)=0.252 \ \ \ Gain(D,触感)=0 \end{aligned} \]

不妨选择色泽作为分类依据

此时决策树为

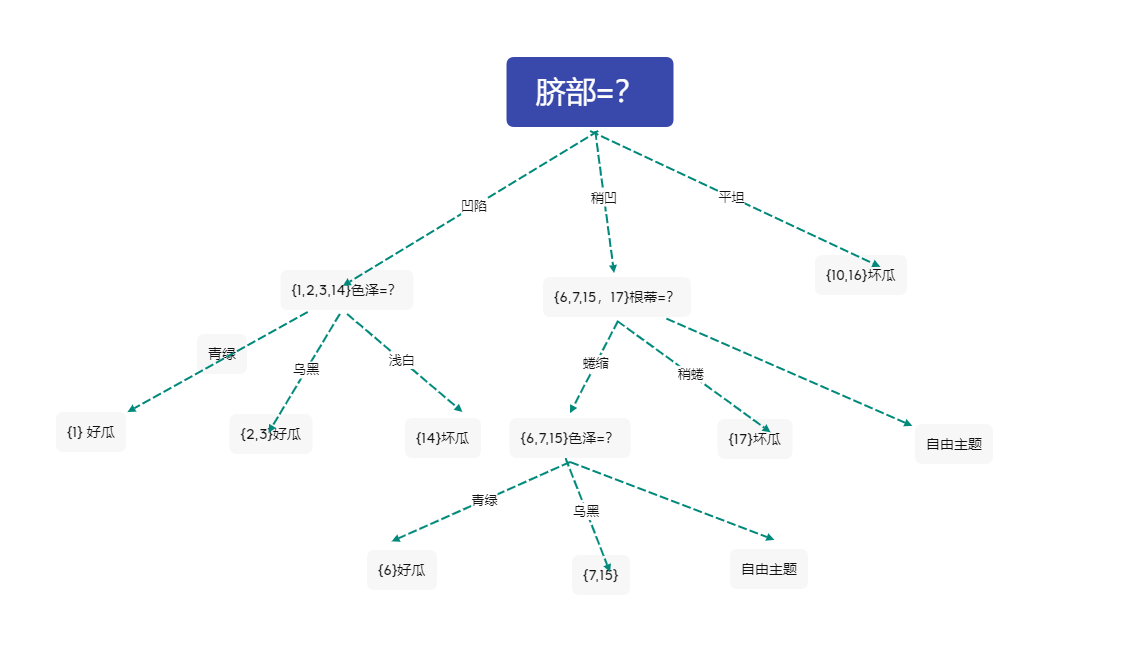
image-20211031214745472

5 对分支\({7,15}\)​进行划分

敲声 信息增益

根据色泽划分为 浊响 一个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\ Ent(D) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1\\ Gani(D,敲声)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 1 - (\frac{2}{2}\times 0.918 ) \\ &= 0 \end{aligned} \]

纹理 信息增益

根据 纹理 划分为 清晰 稍糊 两个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0 \\ Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0\\ Ent(D)&= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\ Gani(D,纹理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 1 - (\frac{1}{2}\times 0+\frac{1}{2} \times 0 ) \\ &= 1 \end{aligned} \]

触感 信息增益

根据触感划分为 软粘 一个子集

计算信息熵

\[\begin{aligned} Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\ Ent(D) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1\\ Gani(D,触感)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\ &= 1 - (\frac{2}{2}\times 0.918 ) \\ &= 0 \end{aligned} \]

选择分类结点构建决策树

\[\begin{aligned} \ \ Gain(D,敲声)=0 \ Gain(D,纹理)=1 \ \ \ Gain(D,触感)=0 \end{aligned} \]

选择纹理作为分类依据

此时决策树为

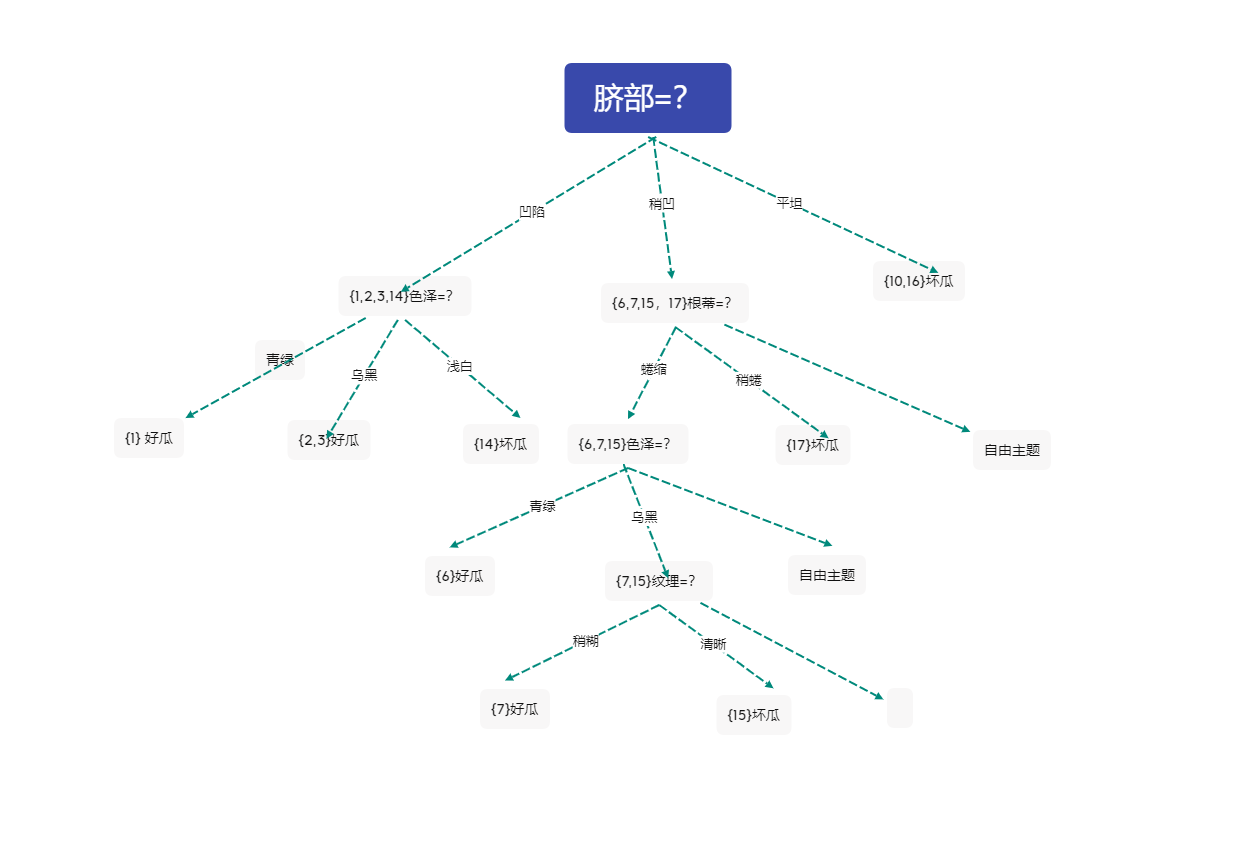
image-20211031215835835

2 决策树后剪枝

1 考虑结点\(7,15\)

原分支（剪枝前），有三个样本被正确分类 验证集精度为 42.8%

剪枝后的决策树

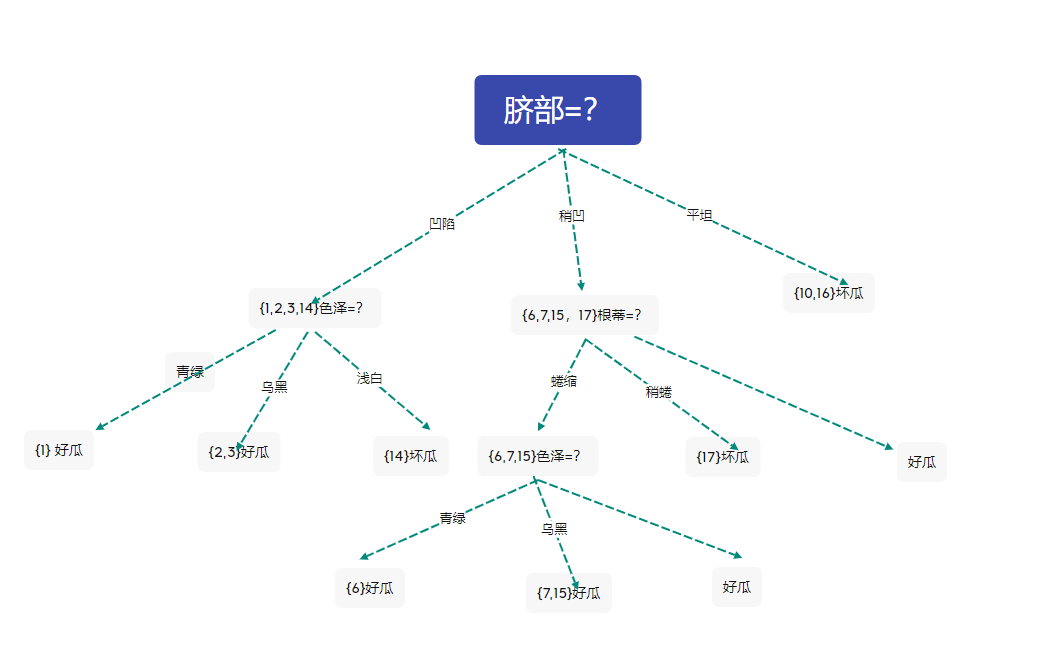
image-20211101090712293

此时验证集有四个样本被正确分类，精度为57.1%

于是后剪枝策略决定剪枝，得到上图的决策树

2 考虑结点\(6,715\)色泽=？

由上图，决策树精度为57.1%

剪去结点后的决策树为

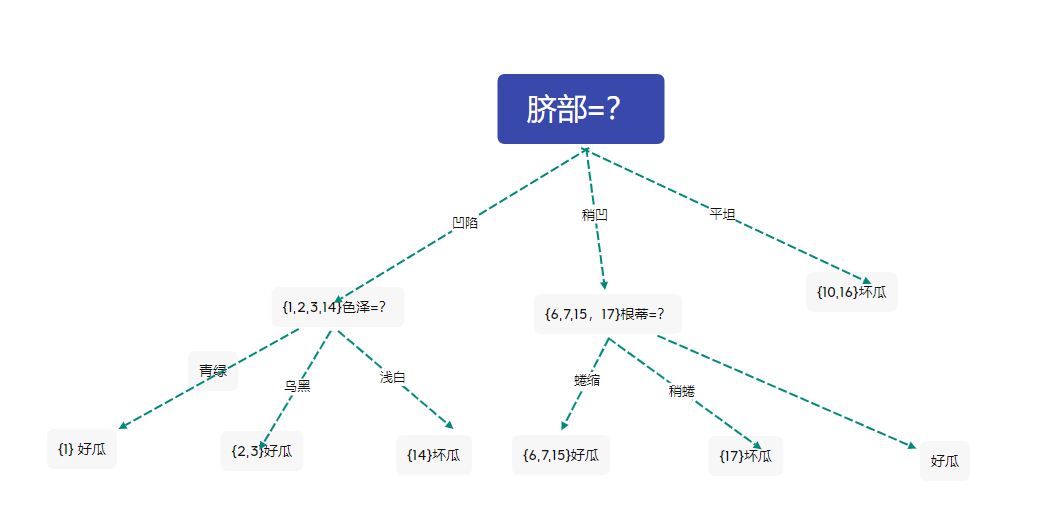
image-20211101091759701

此时验证集有四个样本被正确分类，精度为57.1%

与未剪枝时的精度相同，西瓜书中采用了不剪枝的策略。在这里我们不妨采用剪枝的策略，于是得到上图的决策树

3 考虑结点\(1,2,3,14\)​​色泽=？

在上图基础上来考虑剪去结点\(1,2,3,14\)色泽=？ ，剪枝后的决策树为

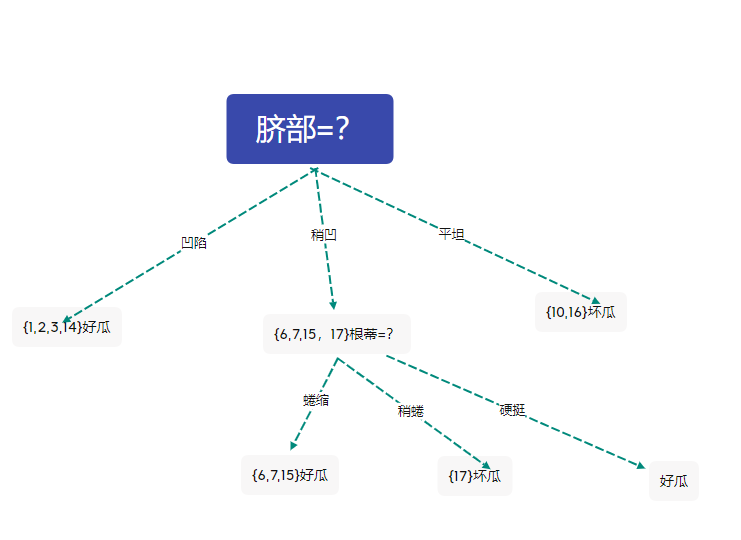
image-20211101092352485

此时的决策树正确分类的样本5个，精度为71.4%

根据后剪枝策略，进行剪枝，得到上图的决策树

4考虑 \(6,7，15,17\)根蒂=？

剪枝后的决策树为

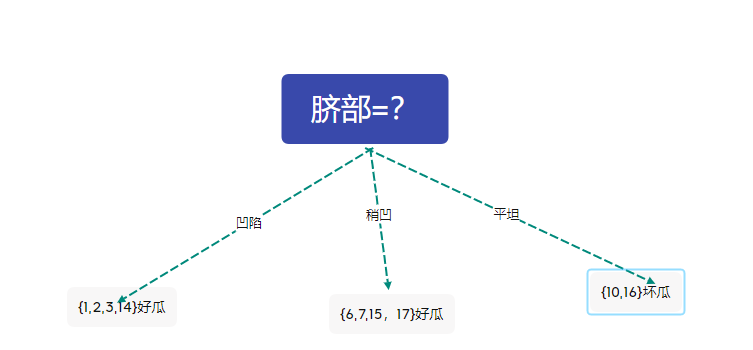
image-20211101092815594

此时的决策树的精度仍然为71.4%

与未剪枝时的精度相同，西瓜书中采用了不剪枝的策略。在这里我们不妨采用剪枝的策略，于是得到上图的决策树

最终得到上图的决策树

posted @ 2021-11-01 09:41  英飞  阅读(1091)  评论(0)  编辑  收藏  举报