高等数学1 函数 极限 连续
https://115.com/s/sw3twip3was#
高等数学
访问码:jc64
复制这段内容,可在115App中直接打开!
函数 极限 连续
函数
函数概念
定义1
给定两个实数集\(D\)和\(M\),若有对应法则\(f\),使对\(D\)内的每一个数\(x\),都有唯一一个数\(y\in M\)与它对应,则称\(f\)是定义在数集\(D\)上的函数。记作
数集\(D\)称为函数\(f\)的定义域。\(x\)所对应的数\(y\)称为\(f\)在点\(x\)的函数值,常记为\(f(x)\)。全体函数值的集合\(f(D)=\{y|y=f(x),x\in D\} (\subset M)\) 称为函数\(f\)的值域。
\(D\rightarrow M\)表示按着法则\(f\)建立数集\(D\)到\(M\)的函数关系。习惯上,我们称此函数关系中的\(x\)为自变量,\(y\)为因变量。
函数的表示
-
公式法
-
列表法
-
图像法
复合函数

复合函数也可以由多个函数相继复合而成
当且仅当\(E^*(\{x|g(x)\in D\}\bigcap E) \neq \emptyset\),函数\(f\)与\(g\)才能复合而成。
反函数

函数\(f\)有反函数,意味着\(f\)是\(D\)与\(f(D)\)之间的一个一一映射。
分段函数
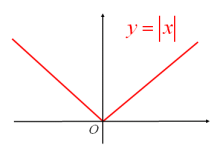
绝对值函数
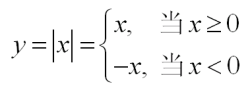
图像
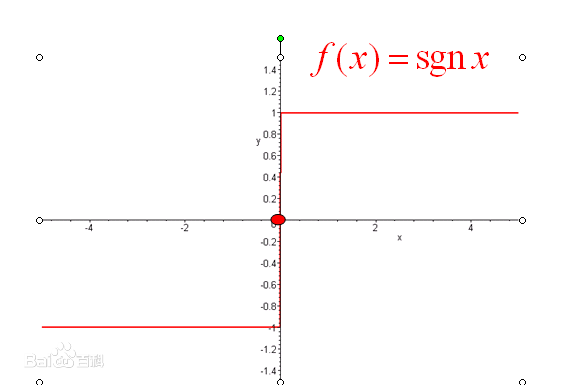
符号函数
定义域为\(D=(-\infin,+\infin)\),值域\(R_f=\{-1,0,1\}\)
\(x=sgnx * |x|\)
图像
取整函数
设\(x\)为任一实数,不超过\(x\)的最大整数称为\(x\)的整数部分,记作\([x]\)。
把\(x\)看做变量,则函数\(y=[x]\) ,称为取整函数。
定义域为\(D=(-\infin,+\infin)\),值域\(R_f=Z\)
图像
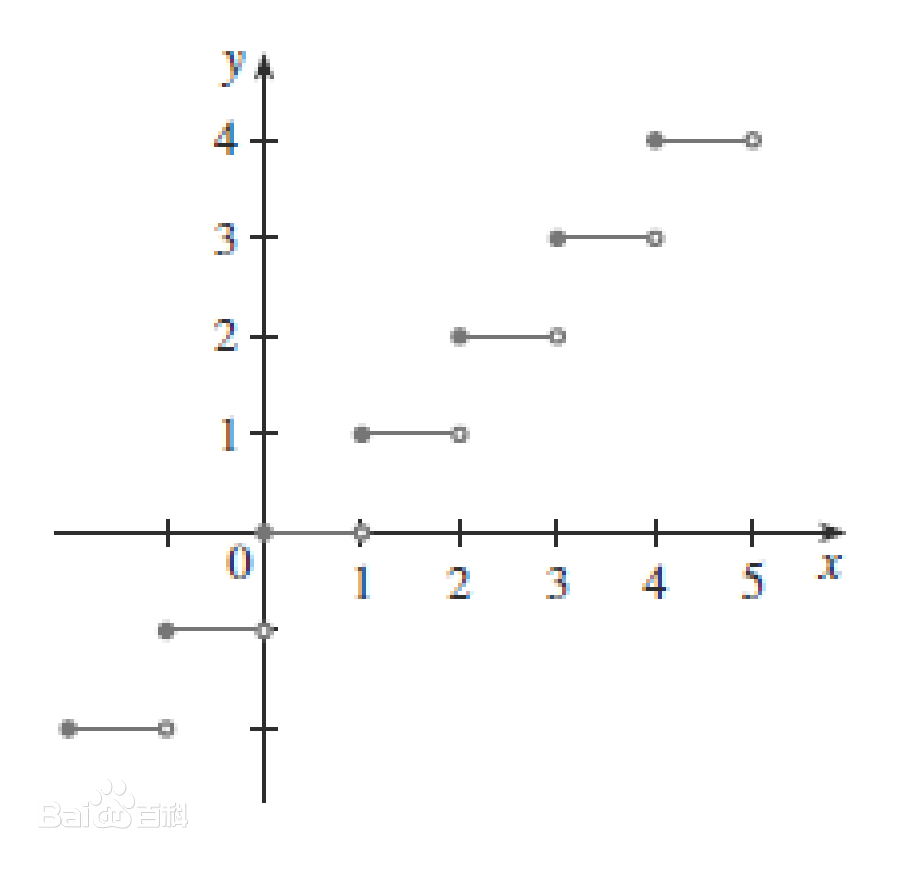
狄利克雷函数
黎曼函数
基本初等函数
-
常量函数 \(y=c(c是常数)\);
-
幂函数 \(y=x^a (a为常数)\);
-
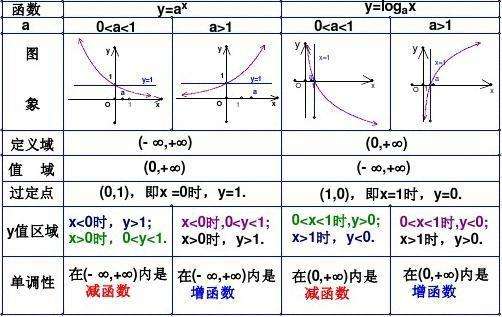
指数函数 \(y=a^x(a>0,a \neq 1)\)
-
对数函数 \(y=log_ax(a>0,a\neq1)\)
-
三角函数
\(y=sinx(正弦函数)\),\(y=cosx(余弦函数)\),
\(y=tanx(正切函数)\),\(y=cotx(余切函数)\)
-
反三角函数
\(y=arsinx(反正弦函数)\),\(y=arcosx(反余弦函数)\),
\(y=artanx(反正切函数)\),\(y=arcotx(反余切函数)\)
指数运算
对于所有实数\(a>0,m,n\),我们有以下恒等式
我们假定\(0^0=1\)
多项式与指数的增长率比较
自然对数\(e\)
对数运算
我们将使用以下记号:
$lgn= log_2n \tag{以2为底的对数} $
$ lnn\tag{自然对数} \$
$ lgkn=(lgn)k\tag{取幂} \$
$ lglgn=lg(lgn)\tag{复合} \$
对所有实数\(a>0,b>0.c>0和m,n\),有
阶乘
记号\(n!\)(读作\(n\)的阶乘)定义为对整数\(n\geq 0\),有
指数函数与对数函数图像
三角函数运算
定义
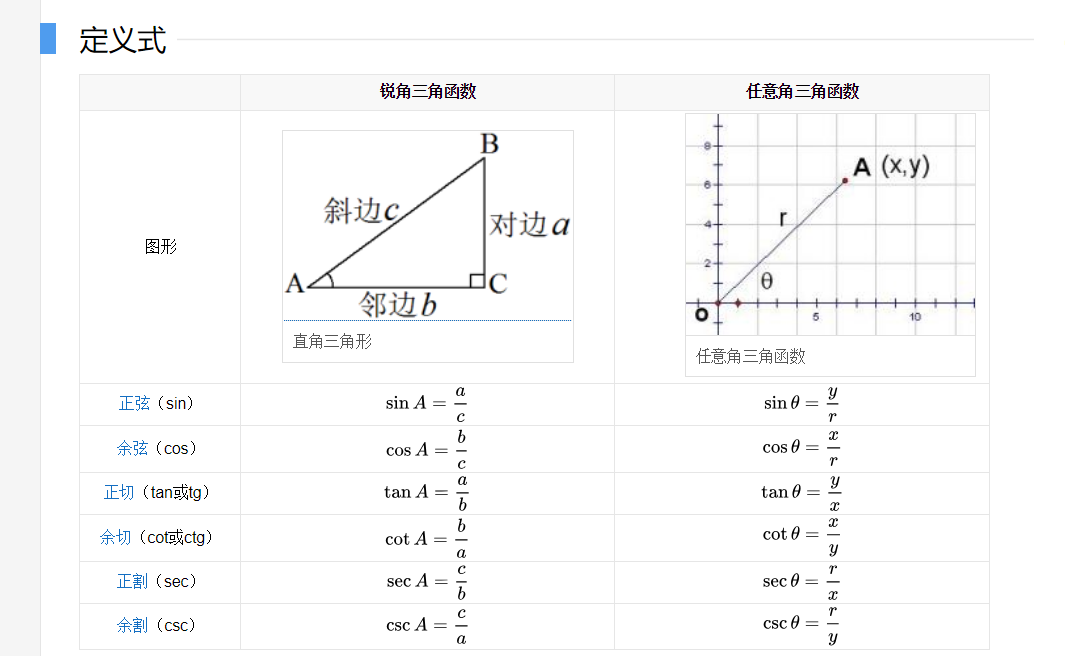
函数关系
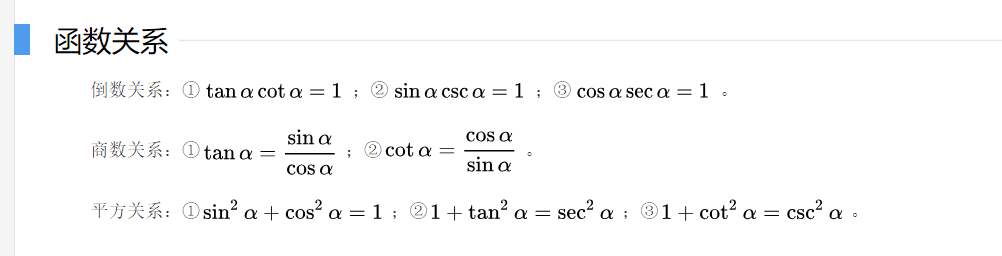

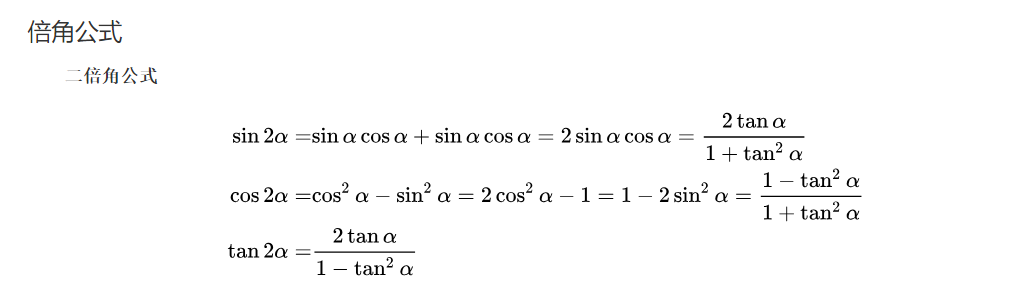


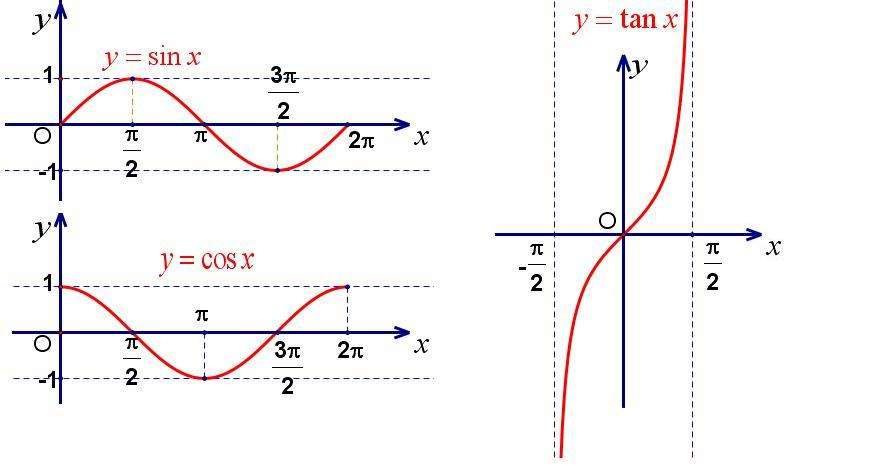
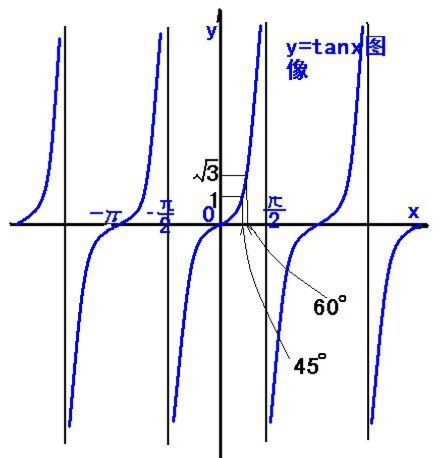
三角函数图像
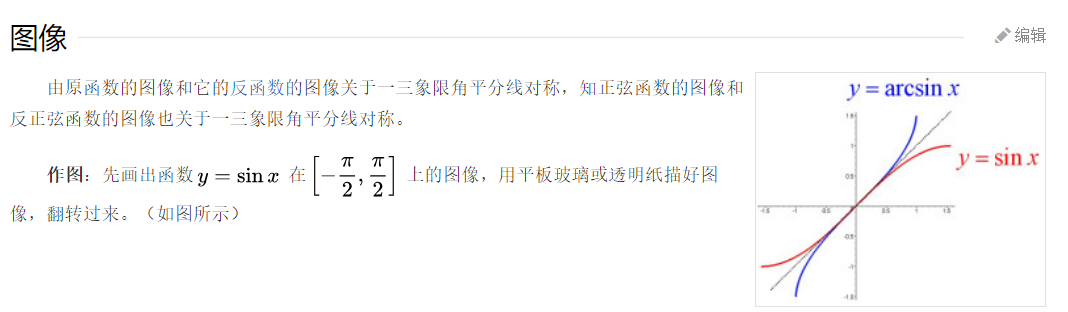
arcsin

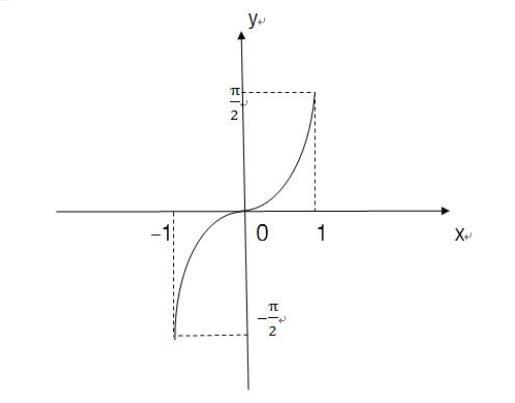




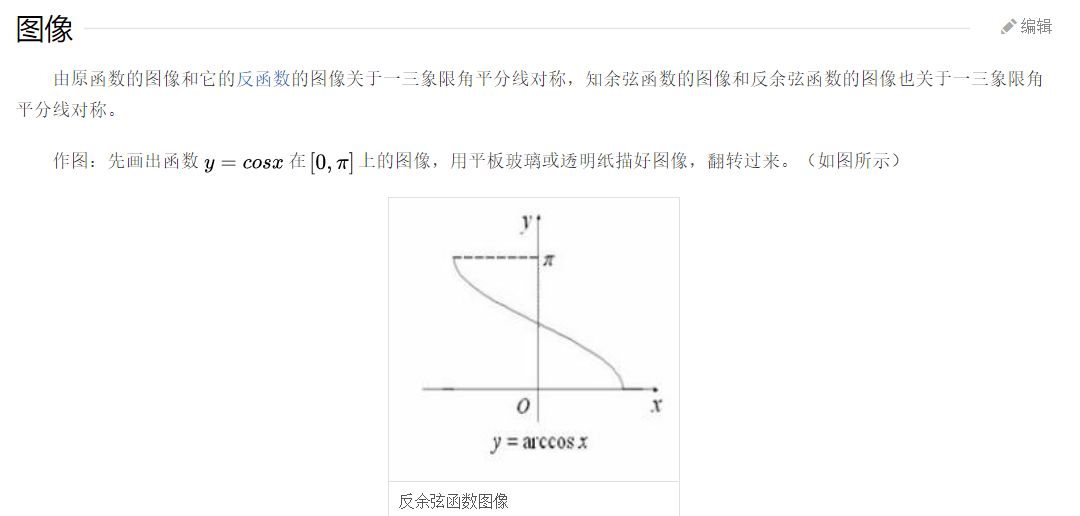
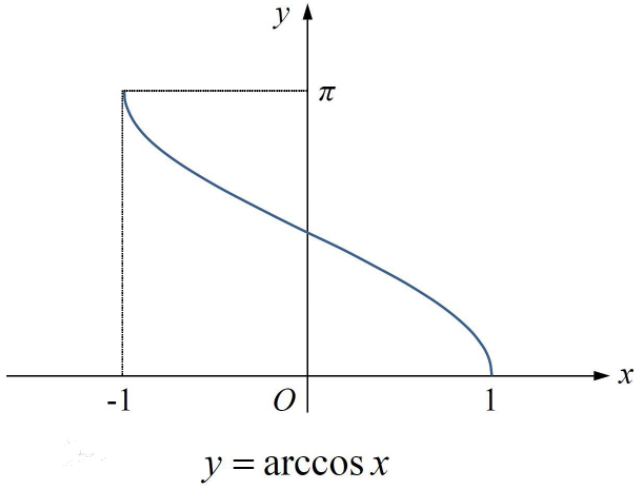
arccos


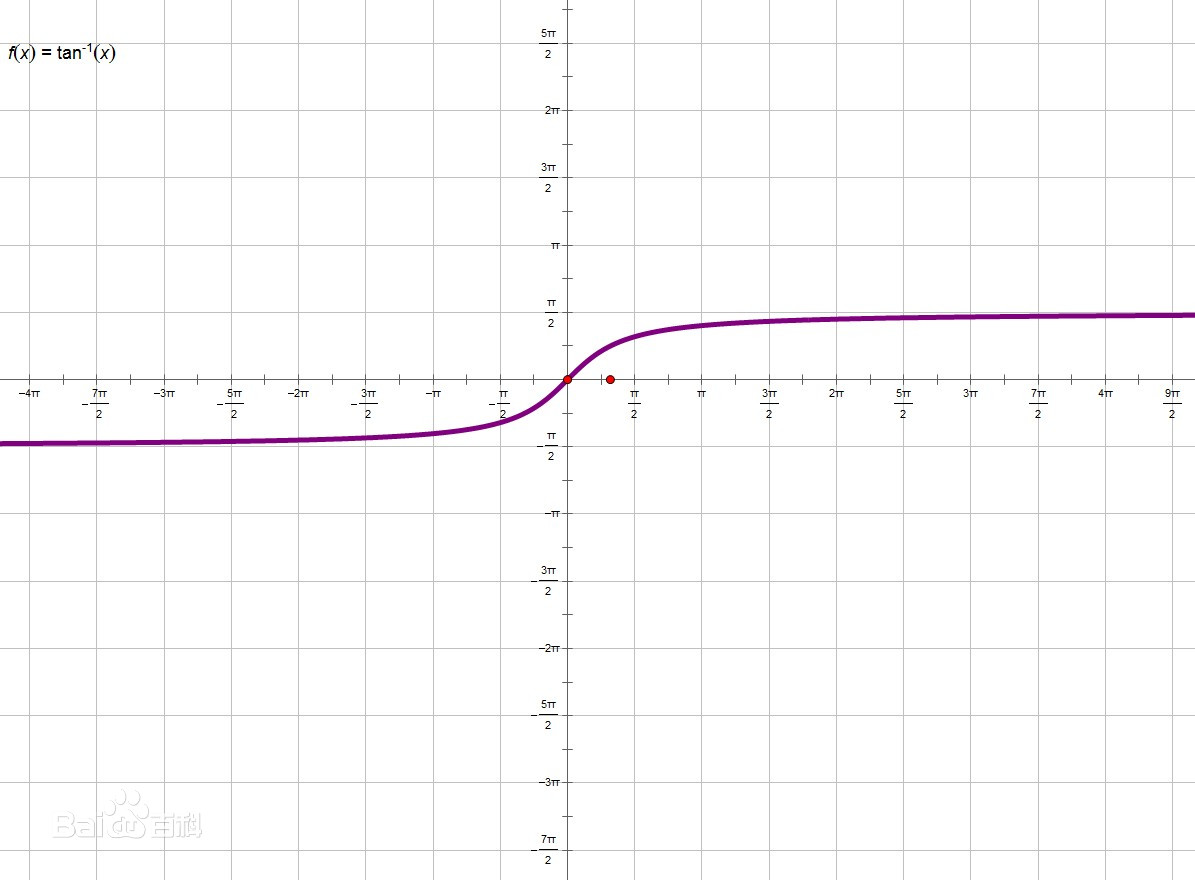
arctan


函数性质
有界性

单调性

奇偶性

周期性
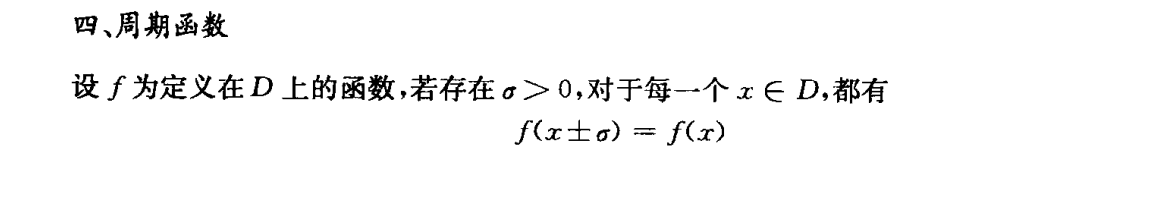
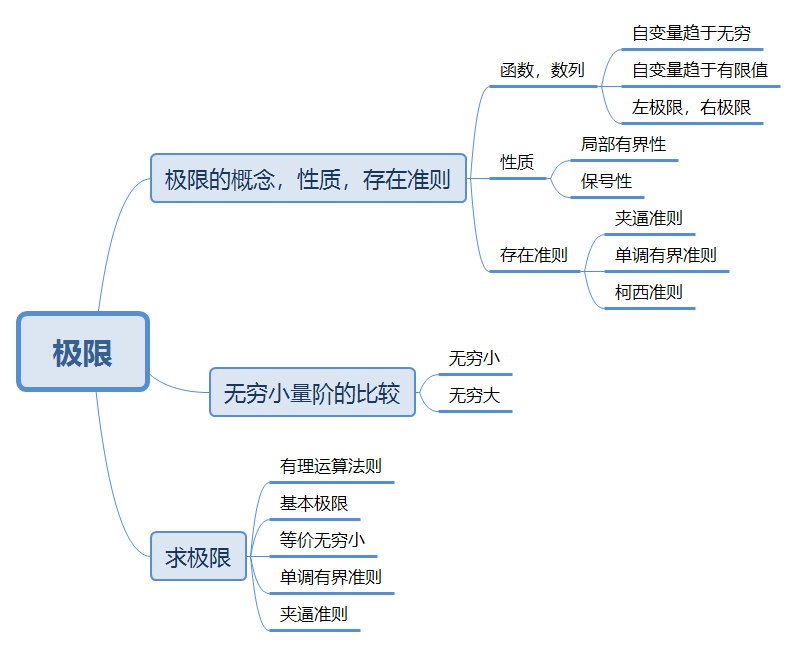
极限
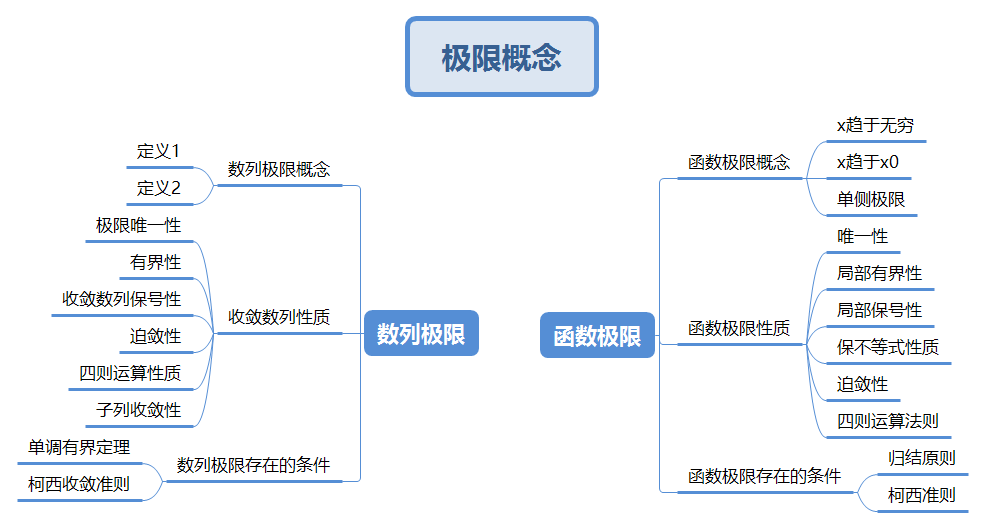
数列极限与函数极限概念性质,存在准则
数列极限
1 数列极限概念


2 收敛数列的性质


3 数列极限存在的条件



函数极限
1 函数极限概念

2 函数极限的性质




3 函数极限存在的条件


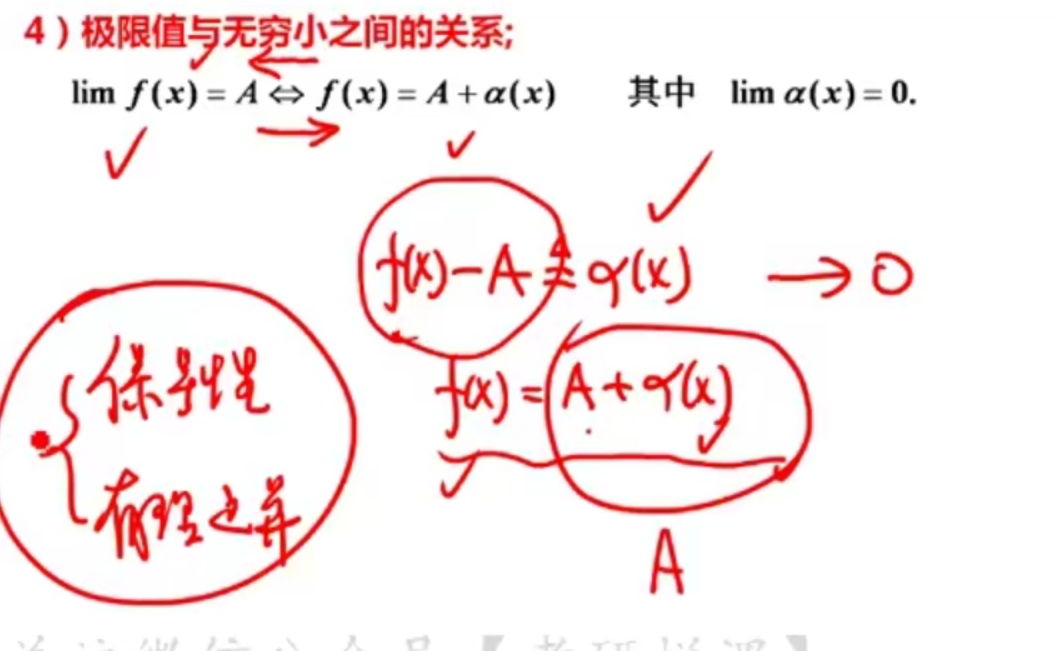
无穷小与无穷大
无穷小

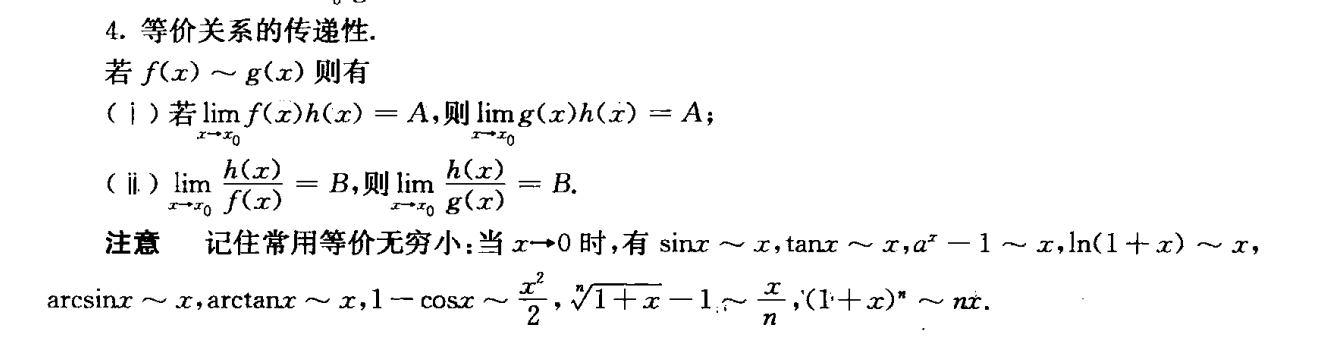
无穷大


极限的计算
两个基本极限
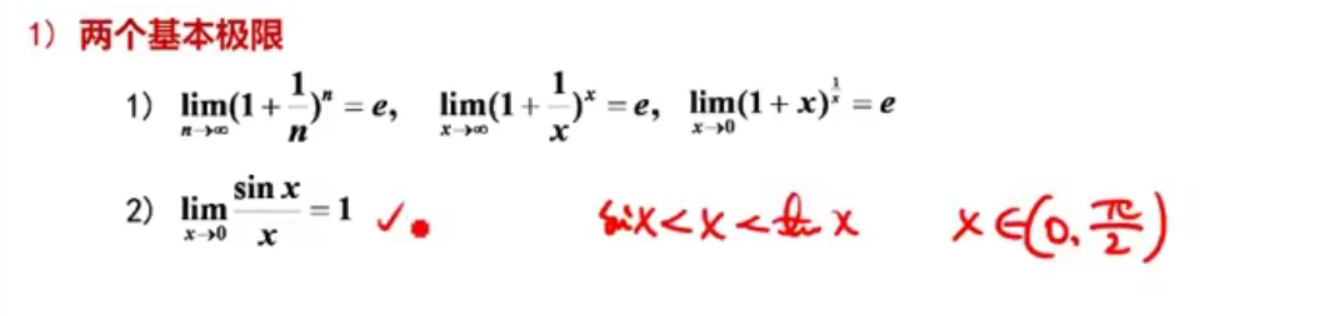
求极限常用方法
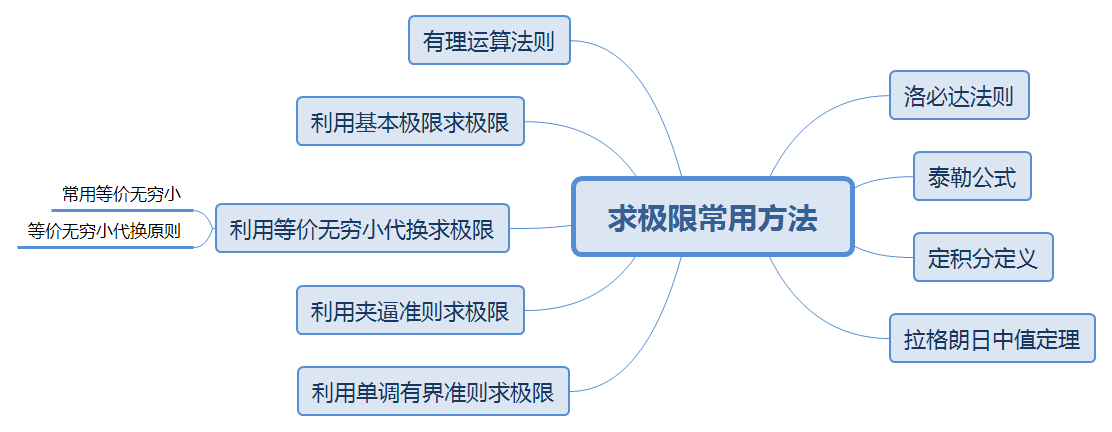
1 有理运算法则


2 利用基本极限求极限

3 等价无穷小的代换


4夹逼准则
5 单调有界准则
常见题型
\(1^{\infty}\)

连续
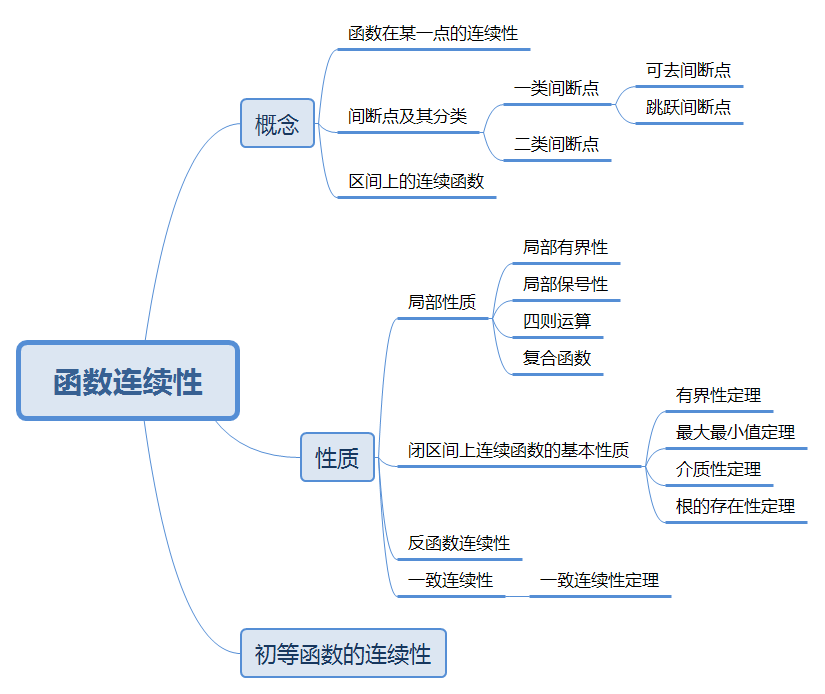
连续性概念
函数在某一点的连续性

间断点
第一类间断点


第二类间断点

区间上的连续函数
若函数\(f\)在区间\(I\)上的每一点都连续,则称\(f\)为\(I\)上的连续函数。对于闭区间或半开半闭区间的端点值,函数在这些点上连续是指左连续或者右连续。
若函数\(f\)在区间\([a,b]\)上仅有有限个第一类间断点,则称\(f\)在\([a,b]\)上分段连续。
连续函数的性质
连续函数的局部性质

闭区间上连续函数的基本性质

反函数的连续性

一致连续性

初等函数的连续性

本文来自博客园,作者:{珇逖},转载请注明原文链接:https://www.cnblogs.com/zuti666/p/13579903.html

