离散数学3 代数结构
离散数学3 代数结构
目录
第九章 代数系统
二元运算及其性质
二元运算

一元运算

二元运算及一元运算的表示

二元运算的性质——算律

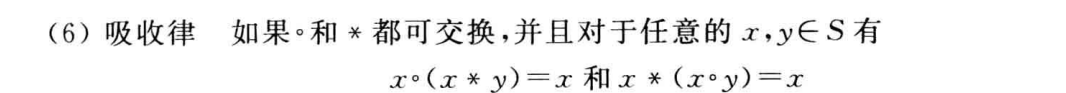
二元运算的特异元素(代数常数)——单位元 零元 可逆元及其逆元

唯一性定理

代数系统

子代数与积代数


代数系统的同态与同构

第十章 群与环
群的定义与性质
半群与独异点

子半群与子独异点


半群与独异点的同态

群的定义

群的性质

群的同态
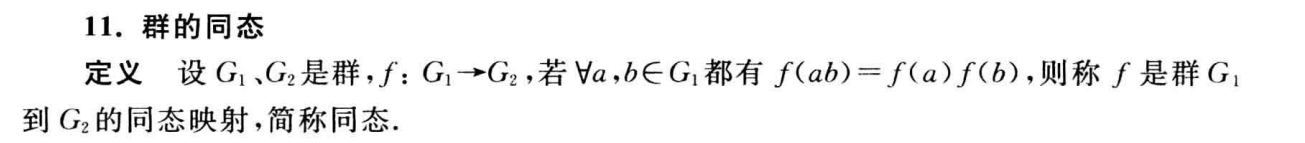
子群与群的陪集分解
子群

右陪集
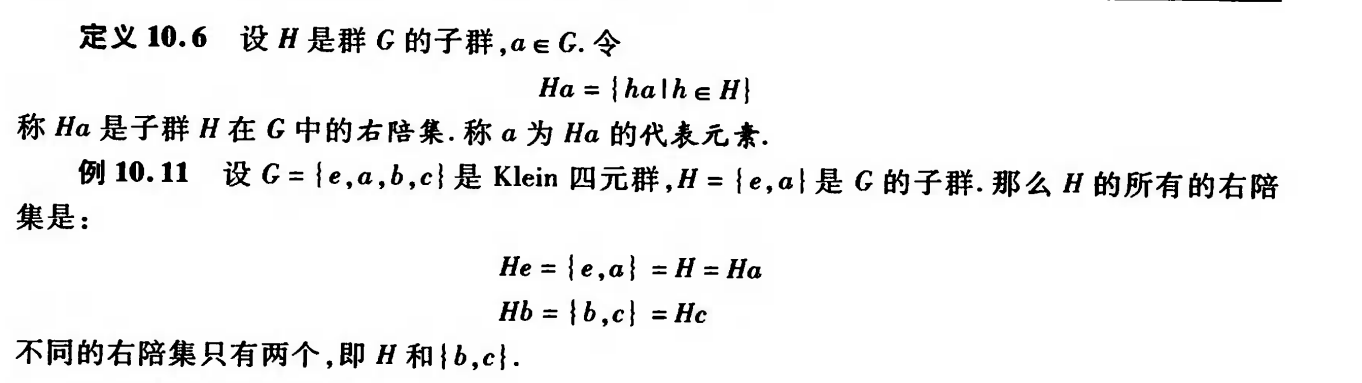
右陪集的性质



划分

\[<G,*>是有限群,<H,*>是<G,*>的子群,则G可以表示成两两不相交的右陪集的并。\\
即存在一个正整数m,使得G=Ha_1\cup Ha_2 \cup \cdots \cup Ha_n ,其中Ha_i \cap Ha_j = \empty ,i \neq j,i,j=1,2,...,n
\]
左陪集

正规子群

指数与拉格朗日定理


循环群与置换群
循环群

置换和置换的乘法


n元置换群

环与域
环的定义

环的运算性质
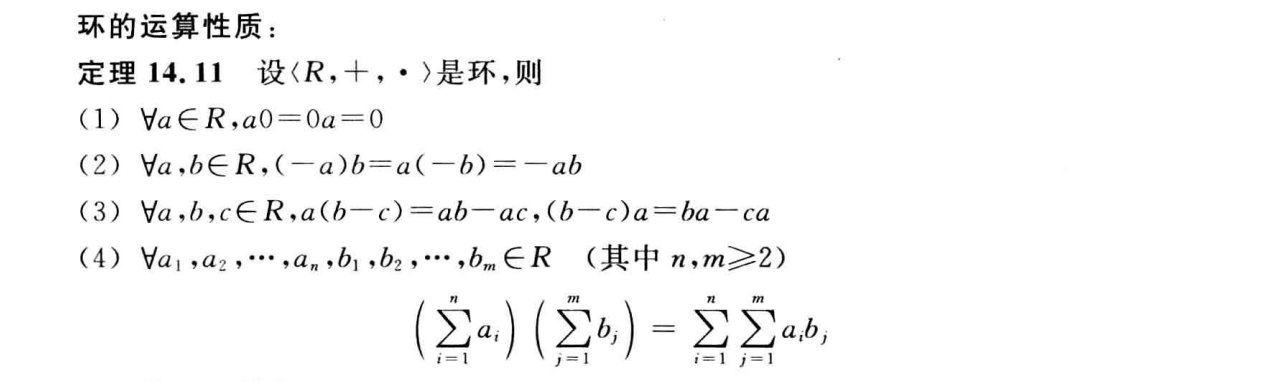
子环定义及判定


环同态

特殊的环

第十一章 格与布尔代数

子格与格同态

特殊的格

布尔代数

本文来自博客园,作者:{珇逖},转载请注明原文链接:https://www.cnblogs.com/zuti666/p/13579847.html

