离散数学2 集合论

合集 - 数学(48)
1.分类算法2.数值计算方法3.离散数学4 组合数学4.离散数学3 代数结构
5.离散数学2 集合论
6.离散数学1 数理逻辑7.离散数学6 初等数论8.高等代数2 向量组9.高等代数1 矩阵10.高等数学2 一元函数微分学11.算法导论 快速排序算法学习12.高等数学3 一元函数积分学13.高等数学1 函数 极限 连续14.离散数学5 图论15.我理解的高等代数——1从方格纸到线性空间16.3 逻辑回归17.朴素贝叶斯18.知识扩展4——拉格朗日乘数，KKT条件，对偶问题19.知识扩展3——广义线性模型GLM20.知识扩展2——熵 ，KL散度，交叉熵，JS散度，Wasserstein 距离（EarthMover距离）21.知识扩展1——最大似然估计22.线性回归23.决策树 机器学习，西瓜书p80 表4.2 使用信息增益生成决策树及后剪枝24.模式识别 第一章 概论25.高等代数9 欧几里得空间26.高等代数7 线性变换27.高等代数6 线性空间28.高等代数5 二次型29.高等代数4 线性方程组30.高等代数3 行列式31.矩阵博弈中的混合策略求解32.博弈论与强化学习实战——CFR算法——剪刀石头布33.博弈论与强化学习——— 基础2 马尔科夫博弈34.博弈论与强化学习——基础1 扩展型博弈35.博弈论与强化学习 算法 一 MinimaxQ, NashQ ,FFQ36.路径规划算法37.博弈论算法 CFR算法38.概率论3 随机变量及其分布39.概率论4 随机变量的数字特征40.频率与概率41.概率论1 随机试验与独立性42.扩展——向量求导43.扩展—— 向量矩阵张量44.我理解的高等代数3——线性变换45.我理解的高等代数——2坐标系变换与矩阵46.集合论1基数—无穷集合元素的个数47.集合论2序数——从自然数系统到无穷集合的排序48.集合论3 公理化—从罗素悖论到集合的公理化定义
收起

离散数学2 集合论

目录

第6章 集合代数

集合的基本概念

  • 集合：把一些事物汇集到一起组成一个整体就称为集合

  • 元素：这些食物就是集合的元素或成员

  • 集合的表示：列举法，概括属性法，文氏图

  • 元素与集合的关系

    • 属于
    • 不属于

  • 同一层级上的两个集合之间的关系

    • 包含，子集

    • 相等

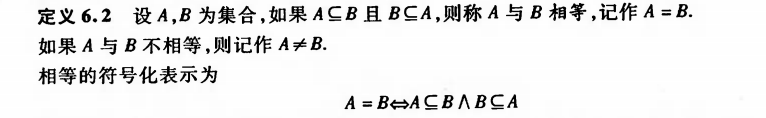
    • 真子集

    • 空集

    • n元集

    • 幂集
      ：

    • 全集

集合的运算

  • 交集

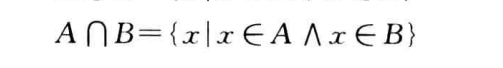
  • 并集

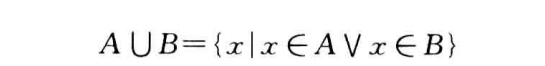
  • 相对补集

  • 对称差集

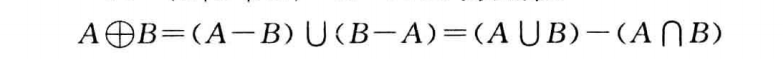
  • 绝对补集

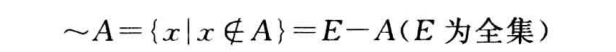
  • 广义并

  • 广义交

    运算的优先顺序

集合恒等式

第7章 二元关系

有序对与笛卡尔积

有序对

笛卡尔积

二元关系

特殊关系

  • 空关系 恒等关系 小于等于关系 整除关系 包含关系

关系的表示

关系的运算

基本运算

关系的幂运算

关系的性质

关系上的性质的判别

关系的闭包

关系闭包的计算公式

等价关系

等价类的性质

商集与划分

偏序关系

偏序集中的元素的可比与覆盖

偏序集中的特殊元素

偏序集的特殊子集

第8章 函数

函数的定义与性质

函数

函数相等

特殊函数

函数的像与完全原像

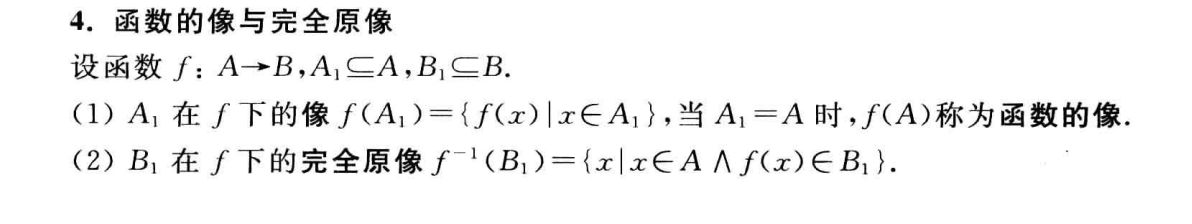
函数的性质

函数的复合和反函数

posted @   英飞  阅读(623)  评论(0)  编辑  收藏  举报
编辑推荐：
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语，封装的思维：从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热？
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列：向量存储与相似性搜索在 .NET 中的实现
阅读排行：
· 10年+ .NET Coder 心语 ── 封装的思维：从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源！
· 周边上新：园子的第一款马克杯温暖上架
点击右上角即可分享
微信分享提示
AI IDE Trae