经典排序算法C++实现

三大基本排序

void insert(vector<int>& a) {
    for (int i = 1; i < a.size();i++) {
        int t = i;
        while (t > 0 && a[t] < a[t - 1]) {
            swap(a[t], a[t - 1]);
            t--;
        }
    }
}//直接插入排序
void insert(vector<int>& a) {
    for (int i = 0; i < a.size()-1;i++) {
        for (int j = 0; j < a.size()-1-i;j++) {
            if (a[j] > a[j + 1])swap(a[j], a[j + 1]);
        }
    }
}//冒泡排序
void pick(vector<int>& a) {
    for (int i = 0; i < a.size()-1;i++) {
        int min=a[i],idx=i;
        for (int j = i+1; j < a.size();j++) {
            if (min > a[j])min = a[j],idx=j;
        }
        swap(a[i], a[idx]);
    }
}//直接选择排序

归并排序

void merge(vector<int>& ans, int L, int mid,int R) {
    vector<int> tmp;
    int i = L, j = mid + 1;
    while (i <= mid && j <= R) {
        if (ans[i] < ans[j])tmp.push_back(ans[i++]);
        else tmp.push_back(ans[j++]);
    }
    while (i <= mid)tmp.push_back(ans[i++]);
    while (j <= R)tmp.push_back(ans[j++]);
    for (int i = L; i <= R;i++) {
        ans[i] = tmp[i - L];
    }
}
void mysort(vector<int> &ans,int L,int R) {
    if (L >= R)return;// 终止递归的条件，子序列长度为1
    int mid = L + (R-L) / 2;// 取得序列中间的元素,防止整数越界
    mysort(ans, L, mid);// 对左半边递归
    mysort(ans, mid + 1, R);// 对右半边递归
    merge(ans, L, mid, R);// 合并
}
优化一：对小规模子数组使用插入排序
用不同的方法处理小规模问题能改进大多数递归算法的性能，因为递归会使小规模问题中方法调用太过频繁，所以改进对它们的处理方法
就能改进整个算法。因为插入排序非常简单，因此一般来说在小数组上比归并排序更快。这种优化能使归并排序的运行时间缩短10%到15%。
怎么切换呢?只要把作为停止递归条件的
 if(L>=R) return;
改成
 if(L>=R+10) { // 数组长度小于10的时候
      InsertSort(int arr[], int low,int high) // 切换到插入排序
      return;
 }
就可以了，这样的话，这条语句就具有了两个功能：
1. 在适当时候终止递归
2. 当数组长度小于M的时候（high-low <= M）， 不进行归并排序，而进行插排

快速排序

//快速排序（从小到大）荷兰国旗问题
void mysort(vector<int> &ans,int L,int R) {
    if (L >= R)return;
    int stan = ans[L],left=L,right=R;
    while (L < R) {
        while (L < R && ans[R] >= stan) R--;//这句和下一句先后顺序是有讲究的
        while (L < R && ans[L] <= stan) L++;        
        if (L < R)swap(ans[L], ans[R]);
    }
    swap(ans[left], ans[L]);//有讲究以后这句调换以后才保证左边都小于基准，右边都大于基准
    mysort(ans, left, L - 1);
    mysort(ans, L+1, right);
}

堆排序

#include <iostream>
using namespace std;
void adjust_heap(int* a, int node, int len){
    int left = 2 * node + 1;
    int right = 2 * node + 2;
    int max = node;
    if (left < len && a[left] > a[max])max = left;
    if (right < len && a[right] > a[max])max = right;
    if (max != node){
        swap(a[max], a[node]);
        adjust_heap(a, max, len);//递归调用，保证子树也是最大堆
    }
}
void heap_sort(int* a, int len){
    for (int i = len / 2 - 1; i >= 0; --i)adjust_heap(a, i, len);
	// 从最后一个非叶子节点（n/2-1）开始自底向上构建，
    for (int i = len - 1; i >= 0; i--){
        swap(a[0], a[i]);           // 将当前最大的放置到数组末尾
        adjust_heap(a, 0, i);       // 将未完成排序的部分继续进行堆排序
    }
}
int main()
{
    int a[10] = { 3, 2, 7, 4, 2, -999, -21, 99, 0, 9 };
    int len = sizeof(a) / sizeof(int);
    for (int i = 0; i < len; ++i)cout << a[i] << ' ';
    cout << endl;
    heap_sort(a, len);
    for (int i = 0; i < len; ++i)cout << a[i] << ' ';
    cout << endl;
    return 0;
}

希尔排序

void insert(vector<int>& ans,int step,int idx) {
    for (int i = idx; i < ans.size(); i+=step) {
        int t = i;
        while (t-step > 0 && ans[t] < ans[t - step]) {
            swap(ans[t], ans[t - step]);
            t=t-step;
        }
    }
}//指定步长的直接插入排序
void mysort(vector<int> &ans) {
    int step = ans.size() / 2;
    while (step!=0) {
        for (int i = 0; i < step;i++) {
            insert(ans, step,i);
        }        
        step /= 2;
    }    
}//初始步长一般取数组长度/2，此后每次减半，一直到一

基数排序

#include <iostream>
#include <vector>
using namespace std;
void fun(vector<int> &ans) {//如果考虑负数可以先同时加上最小负数的绝对值，最后再同时减去这个值
    int min=ans[0];
    vector<int> res(ans.size());
    int len = 3;
    for (int i = 0; i < len;i++) {
        vector<vector<int>> tmp(10,vector<int>());//tmp为模仿桶的二维数组
        for (int j = 0; j < ans.size();j++) {
            int y = pow(10, i);
            tmp[(ans[j]/y) % 10].push_back(ans[j]);//ans数组本身值要保持不变
        }
        res.clear();
        for (int j = 0; j < tmp.size();j++) {
            for (int k = 0; k < tmp[j].size();k++) {
                res.push_back(tmp[j][k]);
            }
        }
        for (int i = 0; i < res.size(); i++) {
            ans[i] = res[i];
        }
    }
    for (int i = 0; i < ans.size(); i++) {//临时数组tmp每位排序后将值赋给原本数组ans
        ans[i] = res[i];
    }
}
int main()
{
    vector<int> ans = { 3, 52, 7, 24, 12, 999, 218, 99, 106, 9 };
    fun(ans);
    for (int i = 0; i < ans.size(); ++i)cout << ans[i] << ' ';
    cout << endl;
    return 0;
}

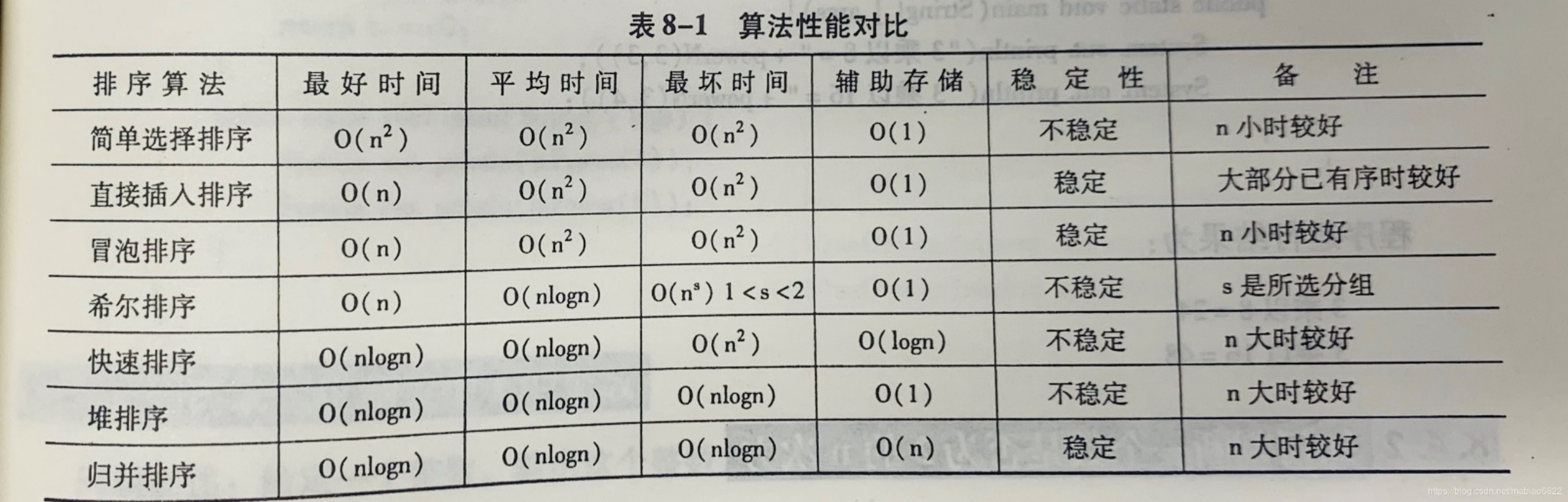
在最好情况下（基本有序），高效的算法是：直接插入排序、冒泡排序。

在无序情况下，高效的算法是：堆排序、快速排序、归并排序。

与初始序列无关的排序算法：简单选择排序。

 

如果给你一个数组，长度很长，综合排序会先进行一个判断，判断数组里面放的数据类型是什么样的，是基础类型(int,double,char,float,short)还是你自定义的类型(student)。

如果装的是基础类型的数据，则会用快排(不稳定)；原因是：基础类型根本不用区分原始顺序，相同值无差异。

 

如果数据的类型是你自己定义的(student)类型，则会用归并排序(稳定)。

原因是：对一个班级，先按照整个分数排序，再按照班级排序，此时相同班级的个体可能是不一样的，是有差别的。

 

如果你的数组长度很短，不管存放的是什么类型的数据，综合排序根本不会选择快排或者归并排序，它会直接用插入排序。

原因是：插入排序的常数项极低，在样本模数小于60的情况下直接用插入排序，为啥？

因为，虽然插入排序是O(N2)的排序，但是当样本量在极小的情况下，O(N2)的劣势表现不出来，反而插入排序的常数项很低，导致在小样本的情况下插入排序会飞快！