TensorFlow学习笔记（二）深层神经网络

一、深度学习与深层神经网络

深层神经网络是实现“多层非线性变换”的一种方法。

深层神经网络有两个非常重要的特性：深层和非线性。

 

1.1线性模型的局限性

线性模型：y =wx+b

线性模型的最大特点就是任意线性模型的组合仍然还是线性模型。

如果只通过线性变换，任意层的全连接神经网络和单层神经网络模型的表达能力没有任何的区别，它们都是线性模型。然而线性模型能够解决的问题是有限的。

如果一个问题是线性不可分的，通过线性模型就无法很好的去分类这些问题。

1.2激活函数实现去线性化

神经元的输出为所有输入的加权和，所以整个神经网络就是一个线性模型。如果将每个神经元的输出通过一个激活函数，那么整个神经网络就变成了一个非线性的模型。

 

 几种常用的非线性激活函数及其图像。

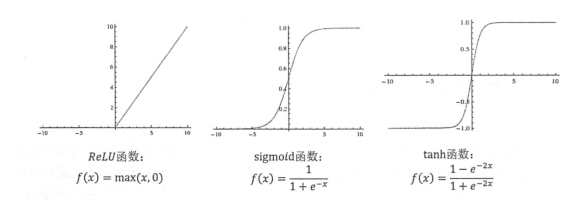
TF提供了7中不同的非线性激活函数，relu，sigmod和tanh是其中最常用的。TF还支持使用自己定义的激活函数。

 

 

 

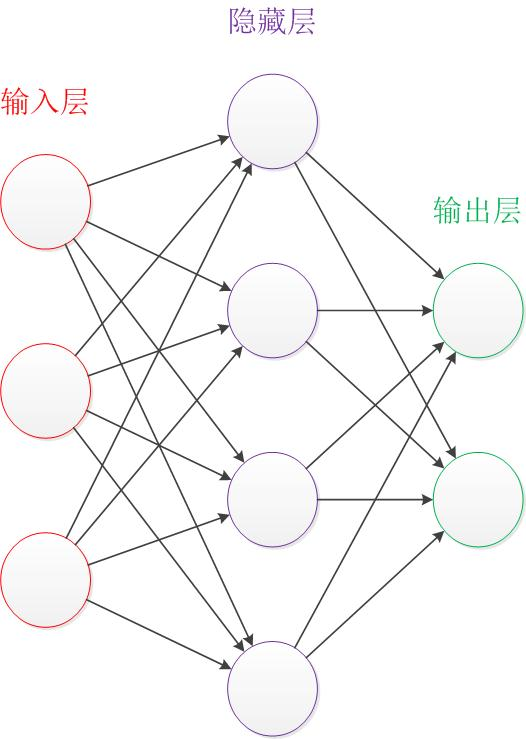
　　　　　　　　这是一个加入了偏置项和激活函数的网络结构。

 那么，怎么用TF实现这个网络结构的前向传播算法呢。

import tensorflow as tf

#声明w1，w2 两个变量,通过seed设定随机种子

w1 = tf.Variable(tf.random_normal([2,3],stddev=1.0 ,seed =1 ))
w2 = tf.Variable(tf.random_normal([3,1],stddev=1.0 ,seed =1 ))
bias1 = tf. Variable(tf.random_normal([3,1],stddev=1.0 ,seed =1 ))
bias2 = tf. Variable(tf.random_normal([1,1],stddev=1.0 ,seed =1 ))

#暂时将输入的誊正向量定义为一个常量，这里的X是一个【1，2】矩阵 x = tf.constant([[0.7,0.9]]) #通过前向传播算法得到输出y h = tf.nn.relu（ tf.matmul(x,w1)+bias1） y =tf.nn.relu（ tf.matmul(h,w2)+bias2）

二 损失函数的定义

神经网络的模型的效果及优化的目标是通过损失函数来定义的。

2.1经典的损失函数

 通过神经网络解决多分类问题最常用的方法就是设置n个输出节点，n为类别的个数。神经网络可以得到一个n维数组作为结果输出。数组中的每一个维度对应一个类别。理想情况，如果一个样本属于类别k，那么这个节点对应的维度为1，其他维度为0.如何判断一个输出向量和期望向量有多接近？可以用交叉熵来判断。

交叉熵的公式：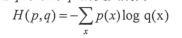 

交叉熵刻画的是两个概率分布之间的距离。将前向计算得到的output经过Softmax优化成一个0~1之间的概率分布。

这样p代表标签值，q代表输出的预测值。

根据公式用TF定义交叉熵的计算图：

cross_entropy = - tf.reduce_mean(y_* tf.log(tf.clip_by_value(y,1e-10,1)))

其中y_表示真实值，y表示模型的预测值。tf.clip_by_value将y的值限制在e^-10 到 1 之间

 因为交叉熵损失一般与softmax回归一起使用，所以TF对这两个功能进行了统一的封装，提供了softmax_cross_entropy_with_logits函数

tf.nn.softmax_cross_entropy_with_logits(y,y_)#y代表原始神经网络的预测输出，y_代表标准答案

 

那么，对于回归问题一般采用什么样的损失函数？

回归问题一般只有一个输出节点，这个节点就是预测值。对于回归问题，最常用的损失函数就是均方误差（MSE），公式如下：

假设一个batch包含n个样本，其中yi是batch中第i个样本的正确答案，yi ‘ 是神经网络输出的预测值。

TF实现MSE：

mse= tf.reduce_mean(tf.square(y_ - y))

均方误差也是分类中一种常用的损失函数。

2.2自定义损失函数

例如我们定义的损失函数为

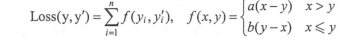
用TF实现

loss = tf.reduce_mean(tf.select(tf.greater(v1,v2),(v1-v2)*a,(v1-v2)*b))

 

tf.greater 比较两个张量中的每一个元素大小，返回比较的结果为元素为True或False的张量。

tf.select 有三个参数，第一个参数为选择条件根据。如果第一个参数为true，就选择第二个参数作为返回值，如果为false就选择第三个参数作为返回值。

 

 三、神经网络优化算法

梯度下降算法用于优化参数，反向传播算法是训练神经网络的核心算法。

梯度下降算法存在两个问题：第一，有可能得到的是局部最优解；第二，每一次迭代的时候，需要计算所有训练数据的loss，计算时间太长了。

所有一般采用mini_batch SGD。

用TensorFlow实现神经网络的优化。

一个伪代码

import tensorflow as tf
batch_size = 128
STEPS = 20000
#每次读取一小部分数据作为当前训练数据来进行BP
x = tf.placeholder(tf.float32,shape=(batch_size,2),name="x_input")
y_ = tf.placeholder(tf.float32,shape=(batch_size,1),name="y_input")
#定义神经网络结构和优化算法
loss = tf.nn.sigmoid_cross_entropy_with_logits()
train_step = tf.train.AdamOptimizer(0.01).minimize(loss)
#训练神经网络
with tf.Session() as ss:
    #参数初始化
    #...
    #迭代的更新参数
    for i in range(STEPS):
        #准备batch_size 个数据
        current_x,current_y = (None,None)
        ss.run(train_step,feed_dict={x:current_x,y_:current_y})

 四、进一步优化神经网络

 有了神经网络的基本算法，在训练的过程中还会遇到一些问题。例如学习率怎么设置，怎么解决过拟合等

下面针对几个问题给出解决办法。

4.1学习率的设置

学习率决定了参数每次更新的幅度。如果学习率过大，那么可能导致参数在极优解的周围震荡，学习不到极优解。如果学习率过小，会导致收敛速度太慢。

为了解决学习率的问题，TensorFlow提供了提供了一种更加灵活的学习率设置方法——指数衰减法。tf.train_exponential_decay函数实现了指数衰减学习率。

global_step = tf.Variable(0)
#通过xponential_decay函数生成学习率
learning_rate = tf.train.exponential_decay(0.1,global_step,100,0.96,staircase=True)
#使用指数衰减的学习率，在minimize函数中传入global_step 将自动更新global_step参数，从而使得学习率也得到相应的更新
learning_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss,global_step=global_step)

staircase=True时，每训练100轮，学习率乘以0.96

4.2过拟合问题

为了避免过拟合问题，一个非常常用的方法就是正则化。正则化的事项就是在损失函数中加入刻画模型复杂度的指标。常用L1正则化和L2正则化。

w = tf.Variable(tf.random_normal([2,1],stddev=1.0,seed=1.0))
lamda = 0.3
y = tf.matmul(x,w)
#lamda是正则化的惩罚系数
loss = tf.reduce_mean(tf.square(y_-y)+tf.contrib.layers.l2_regularizer(lamda)(w))

通过变量来计算损失函数部署很方便，可以通过TF的集合来保存一组实体。例子如下：

import tensorflow as tf
# 获取一层神经网络的权重，并将其L2正则化损失加入名称为“losses”的集合中
def get_weights(shape,lamda):
    #生成变量
    var = tf.Variable(tf.random_normal(shape),dtype=tf.float32)
    tf.add_to_collection("losses",tf.contrib.layers.regularizar(lamda)(var))
    #返回生成的变量
    return var
x = tf.placeholder(tf.float32,shape=[None,2])
y_ = tf.placeholder(tf.float32,shape=[None,1])
batch_size = 8
#定义每一次中节点的个数
layer_dimension = [2,10,10,10,1]
#神经网络的层数
n_layer = len(layer_dimension)
#变量维护前向传播是最深层的节点，最开始是输入层
cur_layer = x
#当前层的节点个数
in_dimension = layer_dimension[0]

#生成5层全连接网络的结构
for i in range(1,n_layer):
    out_diminsion = layer_dimension[i]
    weight = get_weights([in_dimension,out_diminsion],0.001)
    bias = tf.Variable(tf.constant(0.1,shape=[out_diminsion]))
    #使用Relu激活函数
    cur_layer = tf.nn.relu(tf.matmul(cur_layer,weight)+bias)
    #进入下一层之间将下一层的节点个数更新为当前层的节点个数
    in_dimension = layer_dimension[i]

mse_loss = tf.reduce_mean(tf.square(y_ - cur_layer))
#将MSE加入损失集合
tf.add_to_collection("losses",mse_loss)
#get_collection 返回一个列表
loss = tf.add(tf.get_collection("losses"))

 

4.3滑动平均模型

用SGD训练网络时，使用滑动平均模型在很多应用中可以在一定程度提高最终模型在测试数据上的表现。

TF提供了tf.train.ExponentialMovingAverage来实现滑动平均模型。