子集树和排列树

子集树

当所给的问题是从n个元素的集合S中找出满足某种性质的子集时，相应的解空间称为子集树。
比如，01背包问题就是子集树。这类问题通常有2^n个叶子节点，总节点个数是2^(n+1)-1。遍历子集树的任何算法都需要 O(2^n)的时间。

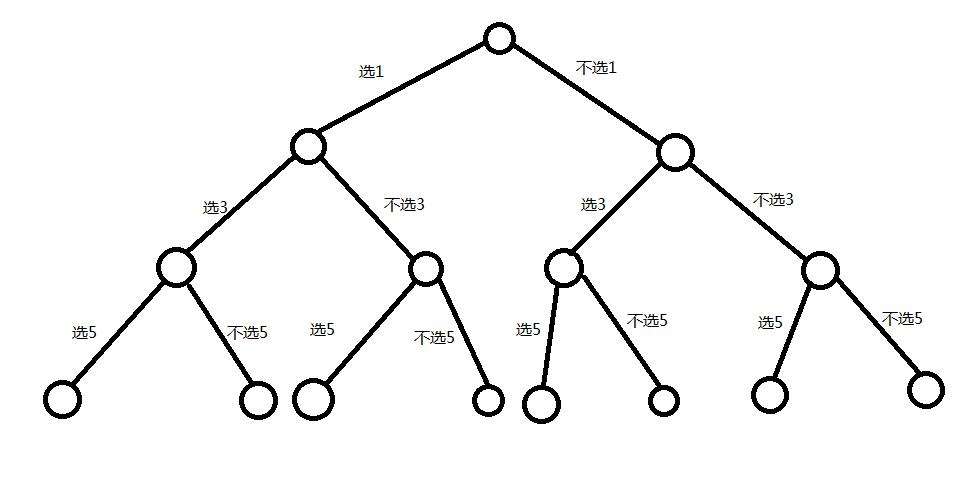
选取数字：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>


void sel(int *arr, int len, int *ass, int index)
{
    if (index == len)
    {
        for (int i = 0; i < len; ++i)
        {
            if (ass[i])
            {
                printf("%d ", arr[i]);
            }
        }
        printf("\n");
    }
    else
    {
        ass[index] = 1;
        sel(arr, len, ass, index+1);
        ass[index] = 0;
        sel(arr, len, ass, index+1);
    }
}


int main()
{
    int arr[] = {1,3,5};
    int len = sizeof(arr)/sizeof(int);

    int *ass = (int*)malloc(len * sizeof(int));
    if (ass)
    {
        sel(arr, len, ass, 0);

        free(ass);
    }

    return 0;
}

 

排列树

当所给问题是确定n个元素满足某种性质的排列时，相应的解空间树称为排列树。

排列树通常有n!个叶子节点。因此遍历排列树需要O(n!)的计算时间

 

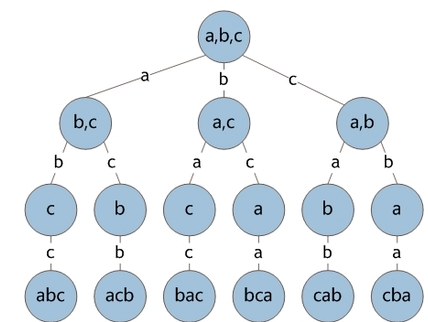
数组全排列：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>


void swap(int *a, int *b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}


void permutation(int *arr, int len, int index)
{
    if (index == len)
    {
        for (int i = 0; i < len; ++i)
        {
            printf("%d ", arr[i]);
        }
        printf("\n");
    }
    else
    {
        for (int i = index; i < len; ++i)
        {
            swap(&arr[index], &arr[i]);
            permutation(arr, len, index+1);
            swap(&arr[index], &arr[i]);
        }
    }
}


int main()
{
    int arr[] = {1,2,3};
    int len = sizeof(arr)/sizeof(int);

    permutation(arr, len, 0);

    return 0;
}