分治法
原理
将问题分解为几个规模较小但类似于原问题的子问题,递归求解这些子问题,然后合并这些子问题的解来建立原问题的解
分治模式在每层递归时,都有三个步骤:
1. 分解原问题为若干子问题,这些子问题是原问题的规模较小的实例。
2. 解决这些子问题,递归地求解各个子问题。如果子问题规模足够小,直接求解
3. 合并子问题的解为原问题的解
归并排序
以归并排序为例,归并排序的操作如下:
分解:分解待排序的n个元素的序列为具有n/2个元素的两个子序列
解决:使用归并排序递归地排序两个子序列
合并:合并两个已排序的子序列以产生已排序的答案
当待排序的序列长度为1时,递归开始回升,在这种情况下不要做任何工作,因为长度为1的序列已排序好了
void mergeArr(int* arr, int startIdx, int mid, int endIdx)
{
int n1 = mid - startIdx;
int n2 = endIdx - mid;
// 用两个临时数组,保存要合并数组的值
int* a1 = new int[n1];
int* a2 = new int[n2];
for (int i = 0; i < n1; i++)
{
a1[i] = arr[startIdx+i];
}
for (int i = 0; i < n2; i++)
{
a2[i] = arr[mid+i];
}
// 按照从小到大的顺序,合并两个数组的值
int len = n1 + n2;
int i = 0, j = 0;
for (int k = startIdx; k < endIdx; k++)
{
if (j == n2)
{
arr[k] = a1[i++];
}
else if (i == n1 || a1[i] > a2[j])
{
arr[k] = a2[j++];
}
else
{
arr[k] = a1[i++];
}
}
delete[] a1;
delete[] a2;
}
// arr表示待排序的数组,startIdx,endIdx分别表示数组中元素的索引,前闭后开区间
void merge_sort(int* arr, int startIdx, int endIdx)
{
if (endIdx - startIdx == 1)
{
return;
}
// 分解
int mid = (startIdx+endIdx) >> 1;
merge_sort(arr, startIdx, mid);
merge_sort(arr, mid, endIdx);
// 合并
mergeArr(arr, startIdx, mid, endIdx);
}
最大子数组问题
以茅台股票的股价走势日线图为例,如下图。假如我们能够穿越时空,回到过去,给你足够买一手茅台的钱,只买卖一次,你怎样可以实现最大化收益。
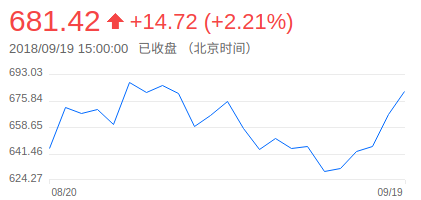
茅台一个月的收盘价:[644.79, 671.49, 667.7, 670.21, 660.3, 687.3, 681.0, 685.85, 680.4, 659.19, 666.21, 675.04, 657.79, 644.0, 650.97, 644.8, 646.0, 630.0, 631.98, 642.9, 645.81, 666.7, 681.42]
一种方法是暴力求解:尝试每对可能的买进和卖出组合,只要卖出日期在买入日期之后即可。n天时间的组合有 n+n-1+n-2+...+1 = O(n^2) 种。
下面使用分治法来求解。
首先变化一下思路,我们将股价每天的变化值列出来,得到一个新的数组:
[26.7, -3.79, 2.51, -9.91, 27.0, -6.3, 4.85, -5.45, -21.21, 7.02, 8.83, -17.25, -13.79, 6.97, -6.17, 1.2, -16.0, 1.98, 10.92, 2.91, 20.89, 14.72]
这样我们原来的问题就转化成:寻找A中最大的非空连续子数组。
分治法三步骤:分解,解决,合并
先把数组分解,假定我们寻找子数组A[low...high]的最大子数组。我们可以找到子数组中央位置mid,然后求解两个子数组A[low...mid]和A[mid+1...high]
A[low...high]的任何连续子数组A[i...j]所处位置有三种情况:
1. 完全位于A[low...mid]中, low <= i <= j <= mid
2. 完全位于A[mid+1...high]中, mid < i <= j <= high
3. 跨越了中点,low <= i <= mid < j <= high
1和2两种情况是原问题的子问题,第3中情况,可以由两个子数组 A[i...mid] 和 A[mid+1...j] 组成。我们只需要找出形如 A[i...mid] 和 A[mid+1...j] 的最大子数组,然后合并就可以了。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
double cross_subarray(double* arr, int low, int mid, int high, int& left, int& right)
{
// 左边的最大子数组,arr[mid]肯定被选中
double leftsum = arr[mid] - 1;
double sum = 0;
for (int i = mid; i >= low; i--)
{
sum += arr[i];
if (sum > leftsum)
{
leftsum = sum;
left = i;
}
}
// 右边的最大子数组,arr[mid]肯定被选中
double rightsum = arr[mid] - 1;
sum = 0;
for (int i = mid; i <= high; i++)
{
sum += arr[i];
if (sum > rightsum)
{
rightsum = sum;
right = i;
}
}
// arr[mid]被计算了两次,减去一次
return leftsum + rightsum - arr[mid];
}
double max_sub_array(double* arr, int low, int high, int& left, int& right)
{
if (low == high)
{
left = right = low;
return arr[low];
}
else
{
int mid = (low + high) >> 1;
int left_low, left_high, right_low, right_high, cross_low, cross_high;
double left_sum = max_sub_array(arr, low, mid, left_low, left_high);
double right_sum = max_sub_array(arr, mid+1, high, right_low, right_high);
double cross_sum = cross_subarray(arr, low, mid, high, cross_low, cross_high);
if (left_sum >= right_sum && left_sum >= cross_sum)
{
left = left_low;
right = left_high;
return left_sum;
}
else if (right_sum >= left_sum && right_sum >= cross_sum)
{
left = right_low;
right = right_high;
return right_sum;
}
else
{
left = cross_low;
right = cross_high;
return cross_sum;
}
}
}
int main()
{
double arr[] = {26.7, -3.79, 2.51, -9.91, 27.0, -6.3, 4.85, -5.45, -21.21, 7.02, 8.83, -17.25, -13.79, 6.97, -6.17, 1.2, -16.0, 1.98, 10.92, 2.91, 20.89, 14.72};
int len = sizeof(arr) / sizeof(double);
int left, right;
double sum = max_sub_array(arr, 0, len-1, left, right);
printf("%d, %d, %lf\n", left, right, sum);
for (int i = left; i <= right; ++i)
{
printf("%lf ", arr[i]);
}
printf("\n");
return 0;
}
打印结果:
17, 21, 51.420000
1.980000 10.920000 2.910000 20.890000 14.720000
如果能往前回几天,可以在9.13号买,今天卖的话,一股赚51.42,一手赚5142
如果能往前回几年,那就无脑买吧,因为茅台的股价走势是这样的:

哈哈,我真能幻想
