快速排序

特点

对于有n个数的数组来说，快速排序最坏情况下的时间复杂度是O(n^2)。但是，快速排序通常是在实际应用中最好的选择，因为它的平均性能非常好: 它的期望时间复杂度是 O(n lgn)，而且，O(n lgn)中隐含的常数因子很小。它还是可以进行原址排序。STL algorithm中的sort函数就是使用快速排序。

过程

快速排序也是使用分治思想。其排序步骤为：

分解：数组 A[p...r] 被划分为两个子数组 A[p...q-1] 和 A[q+1...r]，使得 A[p...q-1]中的每个元素都小于等于A[q]，A[q+1...r] 中的元素都大于 A[q]。

解决：通过快速排序，对两个子数组也排序

合并：因为是子数组是原址排序，所以不需要合并

#include <stdio.h>
#include <stdlib.h>
#include <string.h>


int partition(int* arr, int p, int r)
{
    int key = arr[r];
    int i = p - 1;

    for (int j = p; j < r; j++)
    {
        if (arr[j] < key)
        {
            i++;
            int tmp = arr[i];
            arr[i] = arr[j];
            arr[j] = tmp;
        }
    }
    int tmp = arr[i+1];
    arr[i+1] = arr[r];
    arr[r] = tmp;

    return i+1;
}

void quick_sort(int* arr, int p, int r)
{
    if (p < r)
    {
        int q = partition(arr, p, r);
        quick_sort(arr, p, q-1);
        quick_sort(arr, q+1, r);
    }
}

int main()
{
    int arr[] = {2,4,62,3,4,3,1,7,8,9,5};
    int len = sizeof(arr) / sizeof(int);

    quick_sort(arr, 0, len-1);

    for (int i = 0; i < len; ++i)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");

    return 0;
}

 

quick_sort函数入参表示：数组、开始下标、结束下标。下标都是闭区间。

关键部分是partition函数，《算法导论》中的图：

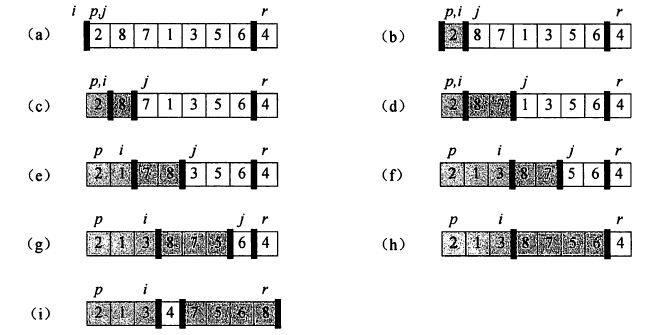
性能

快速排序的运行时间依赖于划分是否平衡。如果划分平衡，时间复杂度O(n lgn)，如果不平衡，时间复杂度 O(n^2)

在最坏情况，就是划分产生的两个子问题分别包含 n-1 个元素和 0 个元素。如果每次递归都出现了这种不平衡，划分操作时间复杂度 O(n).

T(n) = T(n-1) + O(n)

所以时间复杂度为 1+2+3+...+n = O(n^2)

最好情况下，partition得到的两个子问题的规模都不大于n/2.这时，算法运行时间关系是：

T(n) = 2T(n-1) + O(n)

时间复杂度为 O(n lgn)，不过，复杂度的常数因子比堆排序、归并排序都要小

稳定性

快速排序是不稳定的。它可以保证 A[p...q] 的稳定性，但不能保证 A[q...r]的稳定性。

比如数组：[2,7,7,1,1,5,6,4]，快排之后，[2,1,1,4]保持顺序稳定，但是第一个7到了最后一位。