| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | 课程班级博客链接 |
| 这个作业要求链接 | 作业要求链接 |
| 我的课程学习目标 | (1)体验软件项目开发中的两人合作,练习结对编程(Pair programming)。 (2)掌握Github协作开发程序的操作方法。 |
| 这个作业在哪些方面帮助我实现学习目标 | (1)通过该实验练习结对编程 (2)练习github操作方法并掌握 (3)掌握代码编写能力及规范 |
| 结对方学号-姓名 | 201871030109_韩诚 |
| 结对方本次博客作业链接 | 结对方本次博客作业链接 |
| 本项目Github的仓库链接地址 | 项目Github的仓库链接地址 |
任务一:理解并掌握代码风格规范、代码设计规范、代码复审、结对编程概念
1.代码规范

2.代码复审
定义:看代码是否在“代码规范”的框架内正确地解决了问题
代码复审形式:
| 名称 | 形式 | 目的 |
|---|---|---|
| 自我复审 | 自己vs.自己 | 用同伴复审的标准来要求自己 |
| 同伴复审 | 复审者vs.开发者 | 简便易行(最基本复审手段) |
| 团队复审 | 团队vs.开发者 | 有比较严格的规定和流程,适用于关键的代码 |
代码复审目的:
1.找出代码的错误
2.发现逻辑错误
3.发现算法错误
4.发现潜在的错误和回归性错误
5.发现可能需要改进的地方
6.教育开发人员
代码复审步骤:
复审前:
1.代码必须成功编译
2.程序员必须测试过代码
3.程序员必须提供新的代码以及文件差异分析工作。用Windiff或VSTS自带工具都可以
4.面对面复审中,一般是开发者控制流程
5.复审者必须逐一提供反馈意见
6.开发者必须负责让所有的问题都得到满意解释
7.复审意见必须达成一致
复审后:
1.更正明显错误
2.对于无法更正错误在项目管理软件中创建Bug并记录
3.把错误记在“我常犯的错误”表中
3.结对编程
为什么要结对编程?
每人在各自独立设计、实现软件的过程中不免要犯这样那样的错误。在结对编程中,因为有随时的复审和交流,程序各方面的质量取决于一对程序员中各方面水平较高的那一位。这样,程序中的错误就会少得多,程序的初始质量会高很多,这样会省下很多以后修改、测试的时间。具体地说,结对编程有如下的好处:
(1)在开发层次,结对编程能提供更好的设计质量和代码质量,两人合作能有更强的解决问题的能力。
(2)对开发人员自身来说,结对工作能带来更多的信心,高质量的产出能带来更高的满足感。
(3)在心理上, 当有另一个人在你身边和你紧密配合, 做同样一件事情的时候, 你不好意思开小差, 也不好意思糊弄。
(4)在企业管理层次上,结对能更有效地交流,相互学习和传递经验,能更好地处理人员流动。因为一个人的知识已经被其他人共享。
如何结对编程?
(1)驾驶员:写设计文档,进行编码和单元测试等XP开发流程。
(2)领航员:审阅驾驶员的文档、驾驶员对编码等开发流程的执行;考虑单元测试的覆盖程度;是否需要和如何重构;帮助驾驶员解决具体的技术问题。
(3)驾驶员和领航员不断轮换角色,不宜连续工作超过一小时。领航员要控制时间。
(4)主动参与。任何一个任务都首先是两个人的责任,也是所有人的责任。没有“我的代码”、“你的代码”或“她的代码”,只有“我们的代码”。
(5)只有水平上的差距,没有级别上的差异。尽管可能大家的级别资历不同,但不管在分析、设计或编码上,双方都拥有平等的决策权利。
结对编程是个渐进的过程
有效率的结对编程不是一天就能做到的。结对编程是一个相互学习、相互磨合的渐进过程。开发人员需要时间来适应这种新的开发模式。刚开始的结对编程很可能不比单独开发效率更高。但是在度过了学习阶段后,结对编程小组的开发质量、开发时间通常比两人单独开发有明显的改善。
要避免的误区
-
不分情况强迫每个任务都用结对编程的方式, 或者固执地遵守一些教条 (例如 "结对的成员必须水平相当..." 等等)
-
没有提供足够的支持就匆忙上马结对编程 - 工作环境, 硬件, 对结果的期望都要准备好。
-
在具体作法上加入过多限制或要求 - 应该让两位程序员自己决定具体的方式。
不适合结对编程的情况
并不是所有的项目都适合结对编程,下面是一些不适合使用的例子。
1)处于探索阶段的项目,需要深入地研究,在这种情况下,一个人长时间的独立钻研是有必要的。
2)在做后期维护的时候,如果维护的技术含量不高,只需要做有效的复审即可,不必拘泥于形式,硬拉一个人来结对唱二人转。
3)如果验证测试需要运行很长时间,那么两个人在那里等待结果是有点浪费时间。
4)如果团队的人员要在多个项目中工作,不能充分保证足够的结对编程时间,那么成员要经常处于等待的状态,反而影响效率。
5)关键是如何最大限度地发挥“领航员”的作用,如果用处不大,也就无需结对。
两人合作的不同阶段
1.萌芽
2.磨合阶段
3.规范阶段
4.创造阶段
5.解体阶段
两人的合作——如何影响对方
| 方式 | 简介 | 逻辑/感情 | 推/拉 | 注解 |
|---|---|---|---|---|
| 断言 (Assertion) | 就是这样吧,听我的,没错! | 感情 | 推—— 主动推动同伴做某事 | 感情很强烈,适用于有充分信任的同伴。语音、语调、肢体语言都能帮助传递强烈的信息 |
| 桥梁 (Bridge) | 能不能再给我讲讲你的理由…… | 逻辑 | 拉—— 吸引对方,建立共识 | 给双方充分条件互相了解 |
| 说服 (Persuasion) | 如果我们这样做,根据我的分析,我们会有这样的好处,a、 b、 c…… | 逻辑 | 推—— 让对方思考 | 有条理,建立在逻辑分析的基础上。即使不能全部说服,对方也可能接受部分意见 |
| 吸引 (Attraction) | 你想过舒适的生活么?你想在家里发财么?加入我们的传销队伍吧,几个月后就可以有上万元的收入…… | 感情 | 拉—— 描述理想状态,吸引对方加入 | 可以有效地传递信息,但是要注意信息的准确性。夸大的渲染会降低个人的可信度 |
任务二:对结对方《实验二 软件工程个人项目》的项目成果进行评价
| 结对方博客链接 | https://www.cnblogs.com/hc82/p/14599887.html |
| 结对方Github项目仓库链接 | https://github.com/ThreeTeaZ/ThreeTea |
| 符合(1)要求的博客评论 | https://www.cnblogs.com/hc82/p/14599887.html |
clone结对方作业
代码复审的核查表:
| 1.概要部分 | |
|---|---|
| (1)代码能符合需求和规格说明么? | 是 |
| (2)代码设计是否有周全的考虑? | 是 |
| (3)代码可读性如何? | 良好 |
| (4)代码容易维护么? | 容易 |
| (5)代码的每一行都执行并检查过了吗? | 是 |
| 2.设计规范部分 | |
| (1)设计是否遵从已知的设计模式或项目中常用的模式? | 是 |
| (2)有没有硬编码或字符串/数字等存在? | 否 |
| (3)代码有没有依赖于某一平台,是否会影响将来的移植(如Win32到Win64)? | 否 |
| (4)开发者新写的代码能否用已有的Library/SDK/Framework中的功能实现? | 能 |
| (5)在本项目中是否存在类似的功能可以调用而不用全部重新实现? | 是 |
| (6)有没有无用的代码可以清除? | 有 |
| 3.代码规范部分 | |
| (1)修改的部分符合代码标准和风格么(详细条文略)? | 符合 |
| 4.具体代码部分 | |
| (1)有没有对错误进行处理?对于调用的外部函数,是否检查了返回值或处理了异常? | 无 |
| (2)参数传递有无错误,字 | 无 |
| (3)边界条件是如何处理的?Switch语句的Default是如何处理的?循环有没有可能出现死循环? | 无死循环 |
| (4)有没有使用断言(Assert)来保证我们认为不变的条件真的满足? | 无 |
| (5)有没有可能优化? | 有 |
| (6)数据结构中是否有无用的元素? | 有 |
| 5.效能 | |
| (1)代码的效能(Performance)如何?最坏的情况是怎样的? | |
| (2)代码中,特别是循环中是否有明显可优化的部分? | 无 |
| (3)对于系统和网络调用是否会超时?如何处理? | |
| 6.可读性 | |
| 代码可读性如何? | 良好 |
| 7.可测试性 | |
| 代码是否需要更新或创建新的单元测试? | 不需要 |
任务三:开发一款D{0-1}KP 实例数据集算法实验平台
1.需求分析
背包问题(Knapsack Problem,KP)是NP Complete问题,也是一个经典的组合优化问题,有着广泛而重要的应用背景。它的一般描述为:给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为C。问应如何选择装入背包的物品,使得装 入背包中物品的总价值最大?
D{0-1} KP 是经典{ 0-1}背包问题的一个拓展形式,用以对实际商业活动中折扣销售、捆绑销售 等现象进行最优化求解,达到获利最大化。D{0-1}KP数据集由一组项集组成,每个项集有3项物品可 供背包装入选择,其中第三项价值是前两项之和,第三项的重量小于其他两项之和,算法求解过程中, 如果选择了某个项集,则需要确定选择项集的哪个物品,每个项集的三个项中至多有一个可以被选择 装入背包,D{0-1} KP问题要求计算在不超过背包载重量 的条件下,从给定的一组项集中选择满 足要求装入背包的项,使得装入背包所有项的价值系数之和达到最大;D{0-1}KP instances数据 集是研究D{0-1}背包问题时,用于评测和观察设计算法性能的标准数据集。
2.功能介绍
(1)平台基础功能:实验二 任务3;
(2)D{0-1}KP 实例数据集需存储在数据库;
(3)平台可动态嵌入任何一个有效的D{0-1}KP 实例求解算法,并保存算法实验日志数据;
(4)人机交互界面要求为GUI界面(WEB页面、APP页面都可);
(5)查阅资料,设计遗传算法求解D{0-1}KP,并利用此算法测试要求(3);
(6)附加功能:除(1)-(5)外的任意有效平台功能实现。
3.核心代码
1)所需库函数
import matplotlib.pyplot as plt
import linecache
import time
import datetime
import numpy as np
import os
import wx
2)界面类
class MyFrame(wx.Frame):
def __init__(self,parent,id):
wx.Frame.__init__(self, parent,id, title="首页",size=(600,450))
#创建面板
panel = wx.Panel(self)
# 创建文本和输入框
self.title1 = wx.StaticText(panel ,label="D{0-1}KP 实例数据集算法实验平台",pos=(60,20))
#font = wx.Font(14, wx.DEFAULT, wx.FONTSTYLE_NORMAL, wx.NORMAL)
font = wx.Font(16, wx.SWISS, wx.ITALIC, wx.LIGHT)
self.title1.SetFont(font)
self.bt_con = wx.Button(panel,label='登录/注册',pos=(500,20))
self.bt_con.Bind(wx.EVT_BUTTON,self.OnclickSubmit)
self.bt_confirm = wx.Button(panel,label='首 页',pos=(0,90))
self.bt_cancel = wx.Button(panel,label='查看数据',pos=(0,115))
self.bt_cancel = wx.Button(panel,label='动态规划',pos=(0,140))
self.bt_cancel = wx.Button(panel,label='回 溯 法',pos=(0,165))
self.bt_cancel = wx.Button(panel,label='遗传算法',pos=(0,190))
self.bt_cancel = wx.Button(panel,label='降序排列',pos=(0,215))
self.bt_cancel = wx.Button(panel,label='画散点图',pos=(0,235))
self.title2 = wx.StaticText(panel ,label="联系我们",pos=(230,285))
font1 = wx.Font(14, wx.DEFAULT, wx.FONTSTYLE_NORMAL, wx.NORMAL)
#font = wx.Font(16, wx.SWISS, wx.ITALIC, wx.LIGHT)
self.title2.SetFont(font1)
self.title = wx.StaticText(panel ,label="电子邮件:1119786516@qq.com",pos=(180,315))
self.title = wx.StaticText(panel ,label="地址:西北师范大学",pos=(200,340))
self.title = wx.StaticText(panel ,label="邮政编码",pos=(230,365))
self.title = wx.StaticText(panel ,label="联系电话",pos=(230,390))
def OnclickSubmit(self,event):
""" 点击确定按钮,执行方法 """
def fun():
os.system("登录.py")
fun()
3)画散点图
def s1():
weight=list4
profit=list3
plt.figure(figsize=(10, 10), dpi=100)
plt.scatter(weight,profit)
plt.show()
4)遗传算法求解
def s4():
start = time.time()
def init(N,n):
C = []
for i in range(N):
c = []
for j in range(n):
a = np.random.randint(0,2)
c.append(a)
C.append(c)
return C
##评估函数
# x(i)取值为1表示被选中,取值为0表示未被选中
# w(i)表示各个分量的重量,v(i)表示各个分量的价值,w表示最大承受重量
def fitness(C,N,n,W,V,w):
S = []##用于存储被选中的下标
F = []## 用于存放当前该个体的最大价值
for i in range(N):
s = []
h = 0 # 重量
h=int(h)
f = 0 # 价值
f=int(f)
for j in range(n):
if C[i][j]==1:
if h+W[j]<=w:
h=h+W[j]
f = f+V[j]
s.append(j)
S.append(s)
F.append(f)
return S,F
##适应值函数,B位返回的种族的基因下标,y为返回的最大值
def best_x(F,S,N):
y = 0
x = 0
B = [0]*N
for i in range(N):
if y<F[i]:
x = i
y = F[x]
B = S[x]
return B,y
## 计算比率
def rate(x):
p = [0] * len(x)
s = 0
for i in x:
s += i
for i in range(len(x)):
p[i] = x[i] / s
return p
## 选择
def chose(p, X, m, n):
X1 = X
r = np.random.rand(m)
for i in range(m):
k = 0
for j in range(n):
k = k + p[j]
if r[i] <= k:
X1[i] = X[j]
break
return X1
##交配
def match(X, m, n, p):
r = np.random.rand(m)
k = [0] * m
for i in range(m):
if r[i] < p:
k[i] = 1
u = v = 0
k[0] = k[0] = 0
for i in range(m):
if k[i]:
if k[u] == 0:
u = i
elif k[v] == 0:
v = i
if k[u] and k[v]:
# print(u,v)
q = np.random.randint(n - 1)
# print(q)
for i in range(q + 1, n):
X[u][i], X[v][i] = X[v][i], X[u][i]
k[u] = 0
k[v] = 0
return X
##变异
def vari(X, m, n, p):
for i in range(m):
for j in range(n):
q = np.random.rand()
if q < p:
X[i][j] = np.random.randint(0,2)
return X
4.程序测试
1)界面
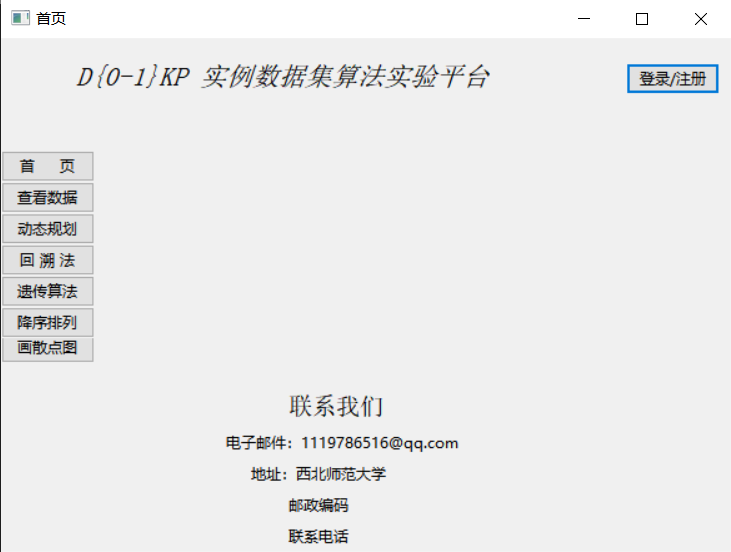
2)降序排序

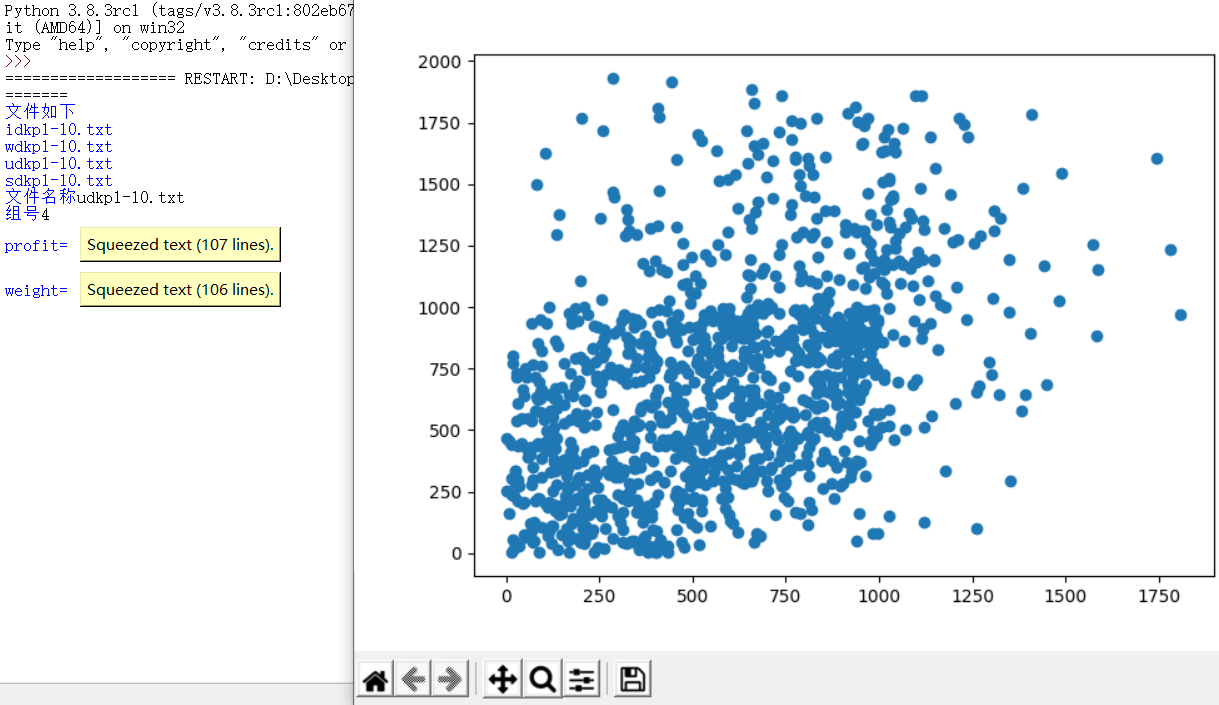
3)画散点图
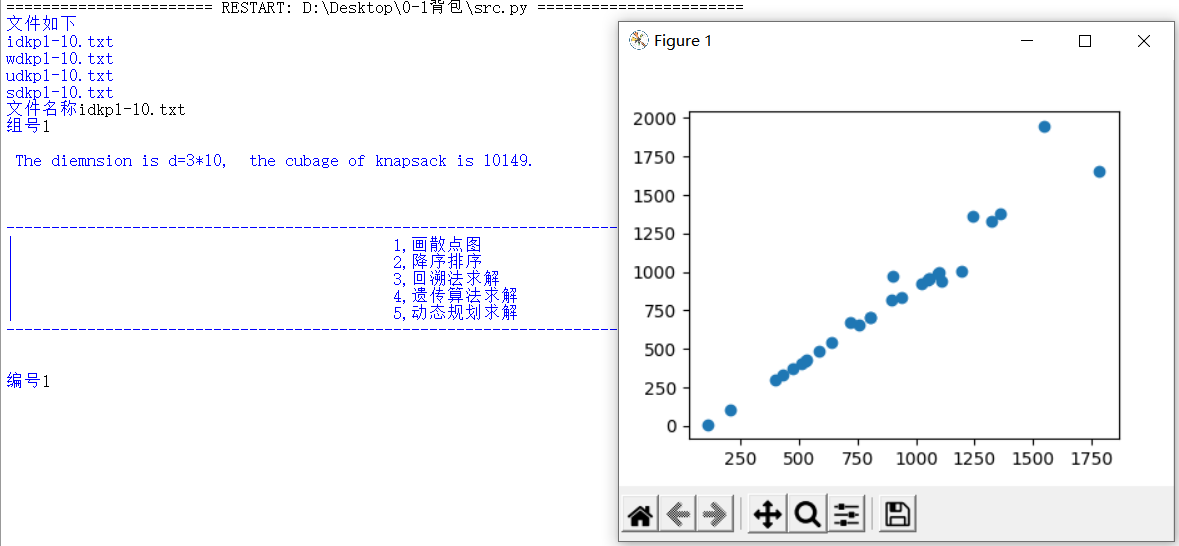
4)回溯法求解

5)遗传算法求解

6)动态规划求解

5.描述结对过程
由于我的结对方为舍友,所以我们都是在一起讨论,并没有在社交软件上进行交流。
6.PSP
| PSP2.1 | 任务内容 | 计划共完成需要的时间(min) | 实际完成需要的时间(min) |
|---|---|---|---|
| Planning | 计划 | 30 | 20 |
| Estimate | 估计这个任务需要多少时间,并规划大致工作步骤 | 30 | 20 |
| Development | 开发 | 450 | 385 |
| Analysis | 需求分析 (包括学习新技术) | 30 | 18 |
| Design Spec | 生成设计文档 | 20 | 15 |
| Design Review | 设计复审 (和同事审核设计文档) | 10 | 6 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 20 | 15 |
| Design | 具体设计 | 100 | 90 |
| Coding | 具体编码 | 180 | 200 |
| Code Review | 代码复审 | 30 | 20 |
| Test | 测试(自我测试,修改代码,提交修改) | 30 | 21 |
| Reporting | 报告 | 60 | 70 |
| Test Report | 测试报告 | 20 | 20 |
| Size Measurement | 计算工作量 | 20 | 20 |
| Postmortem & Process Improvement Plan | 事后总结 ,并提出过程改进计划 | 20 | 30 |
7.实验总结
通过本次实验,我对于github操作方法更加熟悉,并且对PSP的作用有了更深刻的认识,而且通过阅读构建之法学习了代码规范和代码复审的知识,对于结对很有感想,结对以后会有三种效果,1+1<2;1+1=2;1+1>2;我认为这效果主要取决与和结对方的沟通,总的来说,结对做项目利大于弊。



