| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | 课程班级博客链接 |
| 这个作业要求连接 | 作业要求链接 |
| 我的课程学习目标 | (1)掌握软件项目个人开发流程。 (2)掌握Github发布软件项目的操作方法。 |
| 这个作业在那些方面帮助我实现学习目标 | (1)理解PSP流程,形成计划。 (2)熟练GitHub项目托管。 (3)培养良好的代码规范习惯。 |
| 项目GitHub的仓库链接地址 | GitHub的仓库链接地址 |
任务一:作业互评
☀同学一:https://www.cnblogs.com/hc82/p/14549034.html#4842808
☀同学二:https://www.cnblogs.com/nwnuyh/p/14545632.html#4842815
☀同学三:https://www.cnblogs.com/ybp7/p/14540117.html#4842819
☀同学四:https://www.cnblogs.com/yuzehao/p/14548645.html#4842835
任务二:个人开发流程
卡内基梅隆大学(CMU)的能力成熟度模型(CMM和CMMI),是用来衡量一个团队能力的一套模型。CMU专家针对软件工程师也有一套模型,叫Personal Software Process(PSP)。
PSP特点
•不局限于某一种软件技术(如编程语言),而是着眼于软件开发流程,这样开发不同应用工程师可以互相比较。
•不依赖考试,而主要靠工程师自己收集数据,然后分析,提高。
•在小型、初创的团队中,很难找到高质量的项目需求,这意味着给程序员的输入质量不高。这种情况下,程序员输出质量也不高,并不能全部由程序员负责。
•PSP依赖数据。
•PSP目的是记录工程师如何实现需求的效率,而不是记录顾客对产品的满意度。
| PSP2.1 | 任务内容 | 计划共完成需要的时间(min) | 实际完成需要的时间(min) |
|---|---|---|---|
| Planning | 计划 | 30 | 20 |
| Estimate | 估计这个任务需要多少时间,并规划大致工作步骤 | 30 | 20 |
| Development | 开发 | 450 | 385 |
| Analysis | 需求分析 (包括学习新技术) | 30 | 18 |
| Design Spec | 生成设计文档 | 20 | 15 |
| Design Review | 设计复审 (和同事审核设计文档) | 10 | 6 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 20 | 15 |
| Design | 具体设计 | 100 | 90 |
| Coding | 具体编码 | 180 | 200 |
| Code Review | 代码复审 | 30 | 20 |
| Test | 测试(自我测试,修改代码,提交修改) | 30 | 21 |
| Reporting | 报告 | 60 | 70 |
| Test Report | 测试报告 | 20 | 20 |
| Size Measurement | 计算工作量 | 20 | 20 |
| Postmortem & Process Improvement Plan | 事后总结 ,并提出过程改进计划 | 20 | 30 |
任务三:个人项目开发
1,需求分析
背包问题(Knapsack Problem,KP)是NP Complete问题,也是一个经典的组合优化问题,有着广泛而重要的应用背景。它的一般描述为:给定n种物品和一背包。物品i的重量是wi,其价值为vi,背包的容量为C。问应如何选择装入背包的物品,使得装 入背包中物品的总价值最大?
D{0-1} KP 是经典{ 0-1}背包问题的一个拓展形式,用以对实际商业活动中折扣销售、捆绑销售等现象进行最优化求解,达到获利最大化。D{0-1}KP数据集由一组项集组成,每个项集有3项物品可供背包装入选择,其中第三项价值是前两项之和,第三项的重量小于其他两项之和,算法求解过程中,如果选择了某个项集,则需要确定选择项集的哪个物品,每个项集的三个项中至多有一个可以被选择装入背包,D{0-1} KP问题要求计算在不超过背包载重量 的条件下,从给定的一组项集中选择满足要求装入背包的项,使得装入背包所有项的价值系数之和达到最大;D{0-1}KP instances数据集是研究D{0-1}背包问题时,用于评测和观察设计算法性能的标准数据集。
2,求解最优值
3,功能设计
1.读入实验数据文件的有效D{0-1}KP数据;
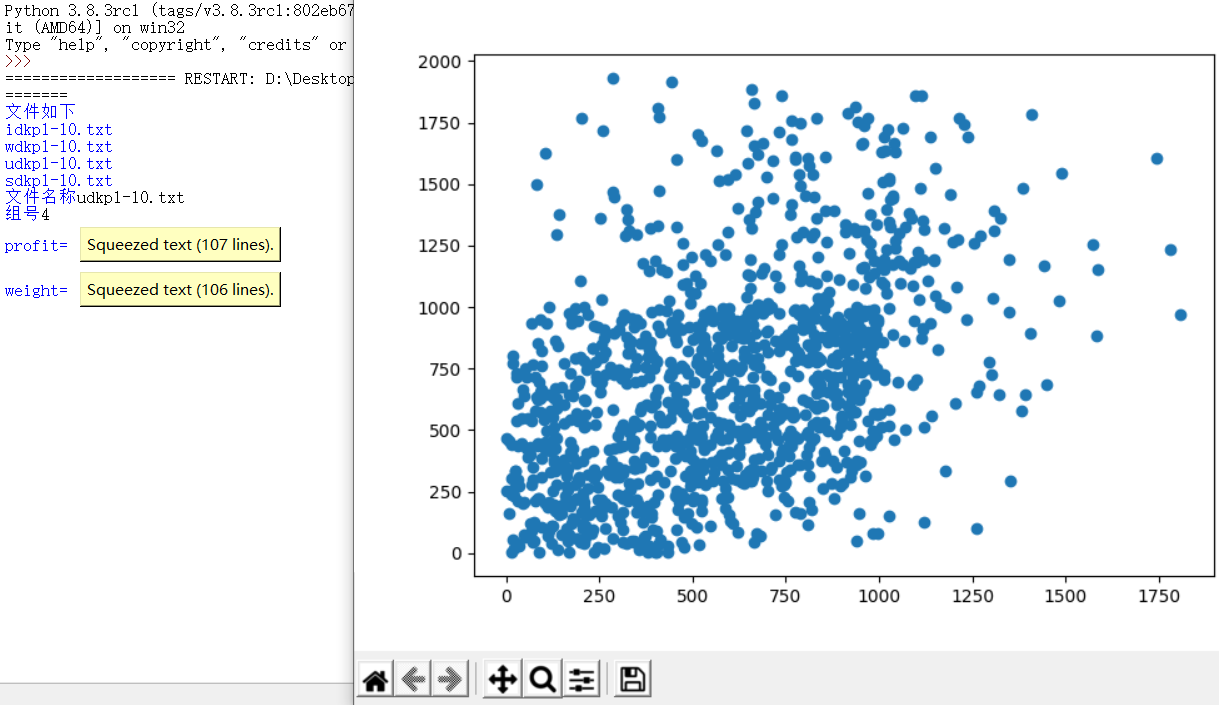
2.绘制任意一组D{0-1}KP数据以重量为横轴、价值为纵轴的数据散点图;
3.对一组D{0-1}KP数据按项集第三项的价值:重量比进行非递增排序;
4.用户能够自主选择动态规划算法、回溯算法求解指定D{0-1} KP数据的最优解和求解时间(以秒为单位);
5.可以将任意一组D{0-1} KP数据的最优解、求解时间和解向量保存为txt文件或导出EXCEL文件。
4,实验测试
读取文件:

绘制散点图:
降序排列:

动态规划解决{0,1}背包问题

回溯法解决{0,1}背包问题

5,代码展示
读取文件
tex=input("文件名称")
n=int(input("组号"))
m=n*8
s=n*8+2
t=n*8-2
profit=linecache.getline(tex,m)
list1 = profit.split(',')
weight=linecache.getline(tex,s)
list2 = weight.split(',')
list1.pop()
list2.pop()
画出散点图并降序排列
weight=list4
profit=list3
plt.figure(figsize=(10, 10), dpi=100)
plt.scatter(weight,profit)
plt.show()
for (a,b) in zip(list3,list4):
num=a/b
lit.append(num)
lit= [round(i,3) for i in lit]
#print(lit)
lit1=sorted(lit,reverse=True)
动态规划解决0-1背包问题
int V_total(int i, int j)
{
if (values[i][j])
return values[i][j]; //如果结果已经计算过,直接返回
int value = 0;
if (i == 0 || j == 0) //当可选物品数量或背包容量为0时,返回0
value = 0;
else if (j < w[i]) //背包容量不足
value = V_total(i - 1, j);
else
{
value = max(V_total(i - 1, j), V_total(i - 1, j - w[i]) + v[i]);
values[i][j] = value;
}
return value;
}
回溯法解决0-1背包问题
def bag_01(weights, values, capicity):
n = len(values)
f = [[0 for j in range(capicity+1)] for i in range(n+1)]
for i in range(1, n+1):
for j in range(1, capicity+1):
f[i][j] = f[i-1][j]
if j >= weights[i-1] and f[i][j] < f[i-1][j-weights[i-1]] + values[i-1]:
f[i][j] = f[i-1][j-weights[i-1]] + values[i-1]
return f
def show(capicity, weights, f):
n = len(weights)
print("最大价值:", f[n][capicity])
x = [False for i in range(n)]
j = capicity
for i in range(n, 0, -1):
if f[i][j] > f[i-1][j]:
x[i-1] = True
j -= weights[i-1]
print("背包中所装物品为:")
for i in range(n):
if x[i]:
print("第{}个,".format(i+1),end='')
if __name__=='__main__':
n=int(input("数量"))
capicity=int(input("容量"))
weights=list4
values=list3
m = bag_01(weights, values, capicity)
show(capicity, weights, m)
7,总结
通过任务一,在互评中互相学习,发现每个人的编写习惯都不一样,通过学习他人良好的编写习惯,完善自己的博客及代码书写规范以及为用户提供良好的视觉效果;任务二主要是学习PSP流程,通过创建PSP,了解自己的欠缺之处,提高效率。对于任务三,发现自己的项目实践很是匮乏,所以完成度很差,希望再以后的学习中再接再厉。
任务四:代码添加到Github账号的项目仓库