gcd()&lcm()背后的故事 | 欧几里得算法
概念:整除,取余,最大公约数,最小公倍数
整除:整数a除以非零整数b,商为整数,余数为0,则a能被b整除,或是b能整除a,记为b|a,整除关系表现了a与b的倍数因数的关系。
取余:整数a除以非零整数b,余数为r,r=a mod b ,mod表示取余,其实可以看做运算符。
如果d|a,d|b,最大的d为最大公约数,d=gcd(a,b)
如果c|a,c|b,最小的c为最小公倍数, d=lcm(a,b)
欧几里得算法
a>b,r=a mod b,a=kb+r推出r=a-kb
d|a,d|b,r=a-kb推出r=xd-kyd进而推出d|r,d|b
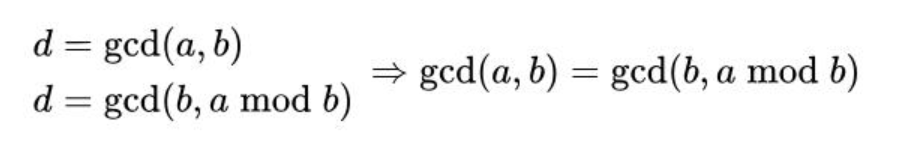

m与0的最大公约数为m,gcd(a,b)=gcd(m,0)=m
int gcd(a,b)
{
return b?gcd(b,a%b):a;
}
最小公倍数,由d|a,d|b推知a=k1d,b=k2d,且gcd(k1,k2)=1(反证法可证),进而最小公倍数为k1k2d
其实就是最大公约数*最小公倍数=两数之积
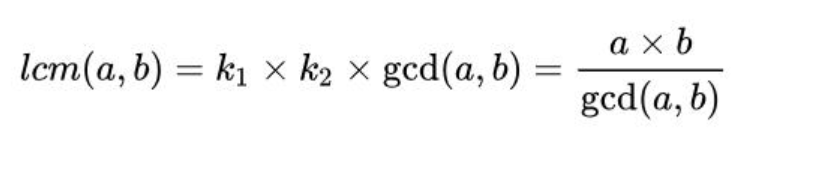
int lcm(a,b)
{
int d;
d=gcd(a,b)
return (a*b)/d; //d*a/d*b/d
}
zer0_1s


