数据结构与算法之线性查找
线性查找
在一个无顺序的数组中找到第k大的元素是几.
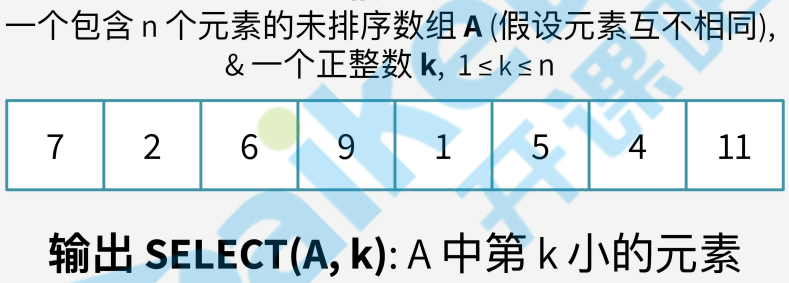
这个问题最简单的解法是先将数组进行排序,然后返回下标k上的元素.如果使用上一节的归并排序则时间复杂度是O(nlogn)
那是否有更好的思路呢.同样我们还是使用分治策略,先从数组中找到一个合适的主元,围绕这个主元划分子数组.比主元小的
划分到左边,比主元大的划分到右边.
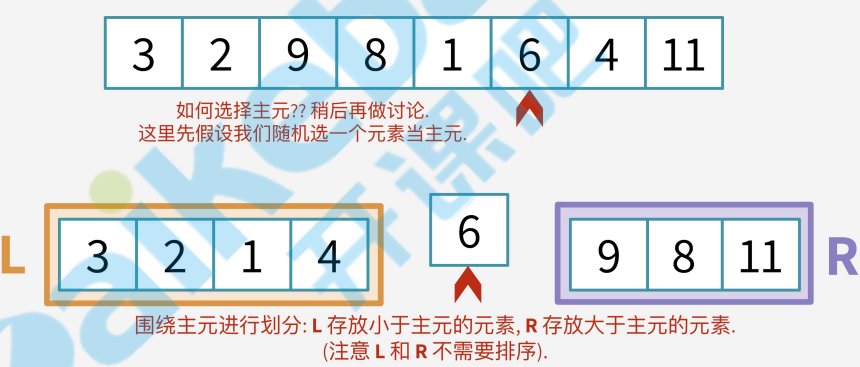
上图为例,假设k是6则要寻找数组中第六个小的元素.那left有4个加上主元1个已经有5个元素了.我们要找的是第六个,很显然,k在right里并且是right中第1小的元素.在right里就是k-left.length+1.此时再次递归
从right中寻找k=1.递归进来第一步依然是选择主元.以此类推
加入k是3则肯定要去left中寻找,并且依然k依然是3.将left进入递归,第一步还是选择主元,以此类推.
最巧的情况是我们选择的主元刚好=k也就是k=5的情况,left4个比主元小.right的3个比主元大,则主元就是k.
所以选择一个合理的主元是很重要的,或者说主元如何能使得left和right能够平衡,这样无论是到left还是right里寻找k都是均衡的.
以下代码选择主元的方式为将数组分为N个小数组,然后获取N个小数中的中位数,然后再在N个中位数中选择一个中位数.所以主元的选择方式为中位数中的中位数.
具体拆分为几个小数组取决于大数组的长度,以下代码大数组的长度为25,所以我拆分成了5*5的小数组.然后从5个小数组中寻找各自的中位数,然后再寻找中位数中中位数.此算法的时间复杂度为O(n)
public class BFPRT_DEMO { public static void swap(int[] A, int i, int j) { if (i == j) return; int temp = A[i]; A[i] = A[j]; A[j] = temp; } // 构造 subMedians 时,寻找每个小数组中的中位数 // 小数组长度之多为 5 public static int findMedianInAtMost5(int[] A, int left, int right) { // 使用插入排序得到每组中的中位数 // 每组长度至多为 5,所以 findMedianInAtMost5 仍为 O(1) int i = left + 1; while (i < right) { int j = i; while (j > left && A[j - 1] > A[j]) { swap(A, j - 1, j); j--; } i++; } return A[(left + right) / 2]; } // 计算 A 数组中的 Median of Medians public static int medianOfMedians(int[] A) { List<Integer> subMedians = new ArrayList<>(); int i = 0; while (i < A.length) { int r = i + 5 > A.length ? A.length : i + 5; subMedians.add(findMedianInAtMost5(A, i, r)); i += 5; } return select(subMedians.stream().mapToInt(Integer::intValue).toArray(), subMedians.size() / 2); } // 线性时间的 Select-K public static int select(int[] A, int k) { if (A.length == 1) { return A[0]; } int pivot = medianOfMedians(A); // Partition 过程 List<Integer> L = new ArrayList<>(); List<Integer> R = new ArrayList<>(); for (int i = 0; i < A.length; i++) { if (A[i] == pivot) continue; else if (A[i] < pivot) L.add(A[i]); else R.add(A[i]); } if (L.size() == k - 1) { return pivot; } else if (L.size() > k - 1) { return select(L.stream().mapToInt(Integer::intValue).toArray(), k); } else { return select(R.stream().mapToInt(Integer::intValue).toArray(), k - L.size() - 1); } } public static void main(String[] args) { // 1 - 25 乱序 int[] A = {1, 14, 4, 18, 25, 6, 17, 9, 3, 5, 10, 16, 12, 23, 19, 13, 20, 8, 15, 24, 7, 21, 22, 2, 11}; for (int i = 1; i <= 25; i++) { // 第 i 小元素为 i System.out.println(select(A, i)); } } }





