数据结构与算法之分治策略
用循环计算两个数字的乘积
用循环解决这个问题只能是类似于小学乘法个位与个位相乘,个位与十位相乘。十位与个位相乘,十位与十位相乘。此算法的时间复杂度为O(n^2)
public static long f1(String n1, String n2) { int sum = 0; for (int i = n1.length() - 1; i >= 0; i--) { for (int j = n2.length() - 1; j >= 0; j--) { //内层 String n = n2.charAt(j) + ""; n = b(n, n2.length() - 1 - j); //外层 String w = n1.charAt(i) + ""; w = b(w, n1.length() - 1 - i); Integer in = new Integer(n); Integer iw = new Integer(w); sum += in * iw; } } return sum; } public static String b(String a1, int a2) { for (int i = a2; i > 0; i--) { a1 += "0"; } return a1; }
分治拆分子任务
分治策略将多位数拆分成个位,只对十以内的数字做乘法操作。以下代码假定S1和S2的长度都是二的次幂,原因是只有长度是而得次幂才能顺利的拆开不会出现三位数拆分的情况。此算法的时间复杂度为O(n^2)
public static BigDecimal exe1(String s1, String s2) { int n = s1.length(); //已经分解成了一位数就相乘 if (n == 1) { BigDecimal b1 = new BigDecimal(s1); BigDecimal b2 = new BigDecimal(s2); return b1.multiply(b2); } //分解两位数 String a1 = s1.substring(0, s1.length() / 2); String a2 = s1.substring(s1.length() / 2); String b1 = s2.substring(0, s2.length() / 2); String b2 = s2.substring(s2.length() / 2); BigDecimal ac = exe1(a1, b1); BigDecimal ad = exe1(a1, b2); BigDecimal bc = exe1(a2, b1); BigDecimal bd = exe1(a2, b2); BigDecimal sn = new BigDecimal("10"); for (int i = 1; i < n; i++) { sn = sn.multiply(new BigDecimal("10")); } BigDecimal sn2 = new BigDecimal("10"); for (int i = 1; i < n / 2; i++) { sn2 = sn2.multiply(new BigDecimal("10")); } BigDecimal mac = ac.multiply(sn); BigDecimal mad = ad.multiply(sn2); BigDecimal mbc = bc.multiply(sn2); BigDecimal r = mac.add(mad).add(mbc).add(bd); return r; }

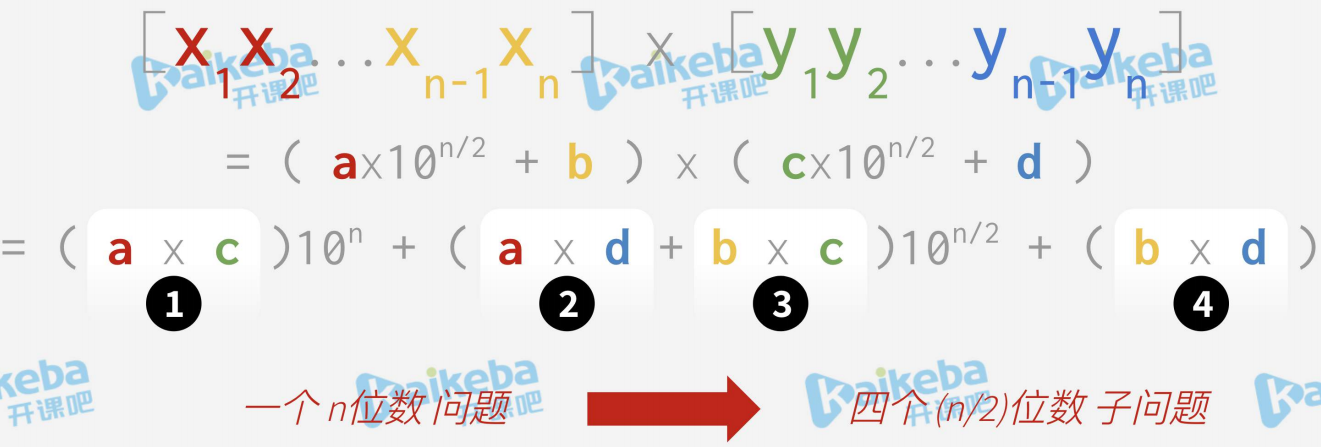
分治拆分子任务(补二次幂)
补二次幂在方法入参新增一个标记,只有第一次进入将原数的长度补成二的次幂,在计算结束后再除以补的数。
public static void main(String[] args) { String s1 = new BigDecimal("534523142").multiply(new BigDecimal("82685675")).toPlainString(); System.out.println(s1); System.out.println("----------------"); String s2 = exe2("534523142", "82685675", true).toPlainString(); System.out.println(s2); System.out.println(s1.equals(s2)); }
/* * s1;乘数 * s2;被乘数 * n: s1或s2补齐后的长度 * b;补数长度,传入0 * f;补齐策略传入true * l:s1或s2补齐后的长度 * */ public static BigDecimal exe2(String s1, String s2, boolean f) { int l = -1; int b = 0; int n = s1.length(); //先补齐,然后再补成二次幂 if (f) { int s1l = s1.length(); int s2l = s2.length(); //两个数长度补齐 if (s1l > s2l) { int c = s1l - s2l; BigDecimal bc = new BigDecimal("10"); for (int i = 1; i < c; i++) { bc = bc.multiply(new BigDecimal("10")); } BigDecimal bs2 = new BigDecimal(s2); s2 = bs2.multiply(bc).toPlainString(); b += c; } else if (s2l > s1l) { int c = s2l - s1l; BigDecimal bc = new BigDecimal("10"); for (int i = 1; i < c; i++) { bc = bc.multiply(new BigDecimal("10")); } BigDecimal bs2 = new BigDecimal(s1); s1 = bs2.multiply(bc).toPlainString(); b += c; } //保证长度是2的次幂 while ((n & (n - 1)) != 0) { s1 += "0"; s2 += "0"; b += 2; n = s1.length(); } n = s1.length(); l = s1.length(); } //已经分解成了一位数就相乘 if (n == 1) { BigDecimal b1 = new BigDecimal(s1); BigDecimal b2 = new BigDecimal(s2); return b1.multiply(b2); } //分解两位数 String a1 = s1.substring(0, s1.length() / 2); String a2 = s1.substring(s1.length() / 2); String b1 = s2.substring(0, s2.length() / 2); String b2 = s2.substring(s2.length() / 2); BigDecimal ac = exe2(a1, b1, false); BigDecimal ad = exe2(a1, b2, false); BigDecimal bc = exe2(a2, b1, false); BigDecimal bd = exe2(a2, b2, false); BigDecimal sn = new BigDecimal("10"); for (int i = 1; i < n; i++) { sn = sn.multiply(new BigDecimal("10")); } BigDecimal sn2 = new BigDecimal("10"); for (int i = 1; i < n / 2; i++) { sn2 = sn2.multiply(new BigDecimal("10")); } BigDecimal mac = ac.multiply(sn); BigDecimal mad = ad.multiply(sn2); BigDecimal mbc = bc.multiply(sn2); BigDecimal r = mac.add(mad).add(mbc).add(bd); //排除补齐的 if (n == l && b != 0) { BigDecimal mr = new BigDecimal("1"); for (int i = 0; i < b; i++) { mr = mr.multiply(new BigDecimal("10")); } r = r.divide(mr); } return r; }





