回归+内插

回归

1.polyfit()线性拟合

对形如f(x)=ax+b f(x)=ax^2+bx+c f(x)=ax^3+bx^2+cx+d 可以得到最优的参数

>> x=[-1.2 -0.5 0.3 0.9 1.8 2.6 3.0 3.5];
y=[-15.6 -8.5 2.2 4.5 6.6 8.2 8.9 10.0];
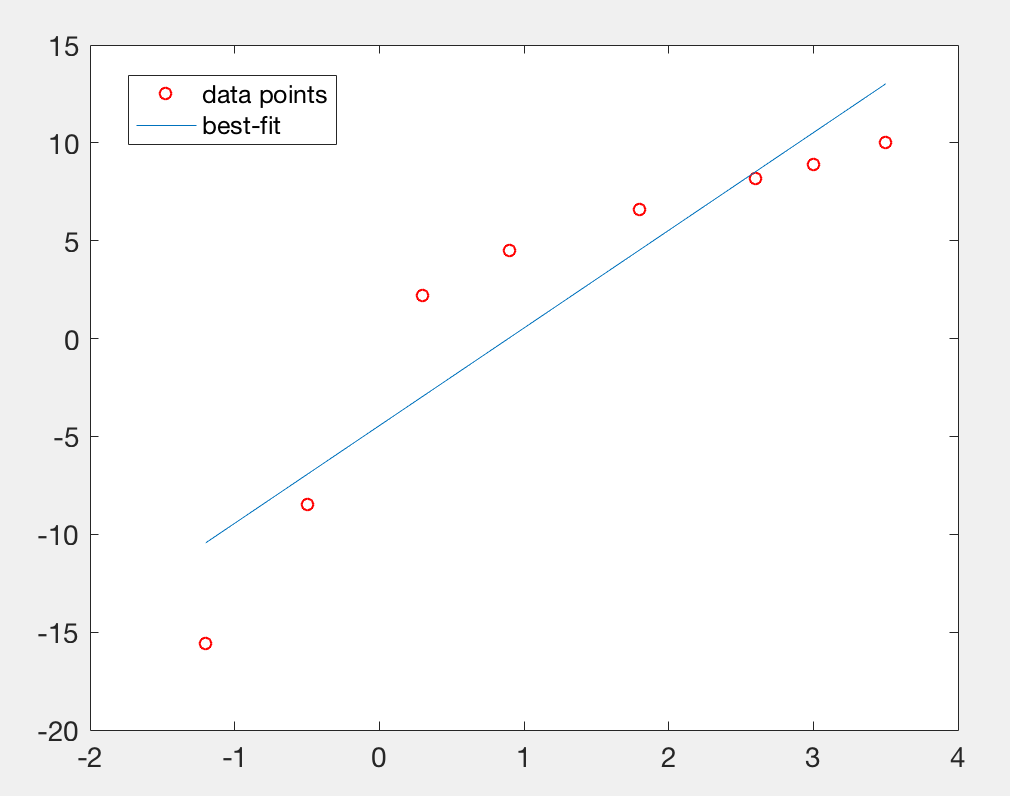
fit=polyfit(x,y,1);
>> xfit=[x(1):0.1:x(end)];
>> yfit=fit(1)*xfit+fit(2);
>> plot(x,y,'ro',xfit,yfit);
>> set(gca,'fontsize',14)
>> legend('data points','best-fit')

 

 

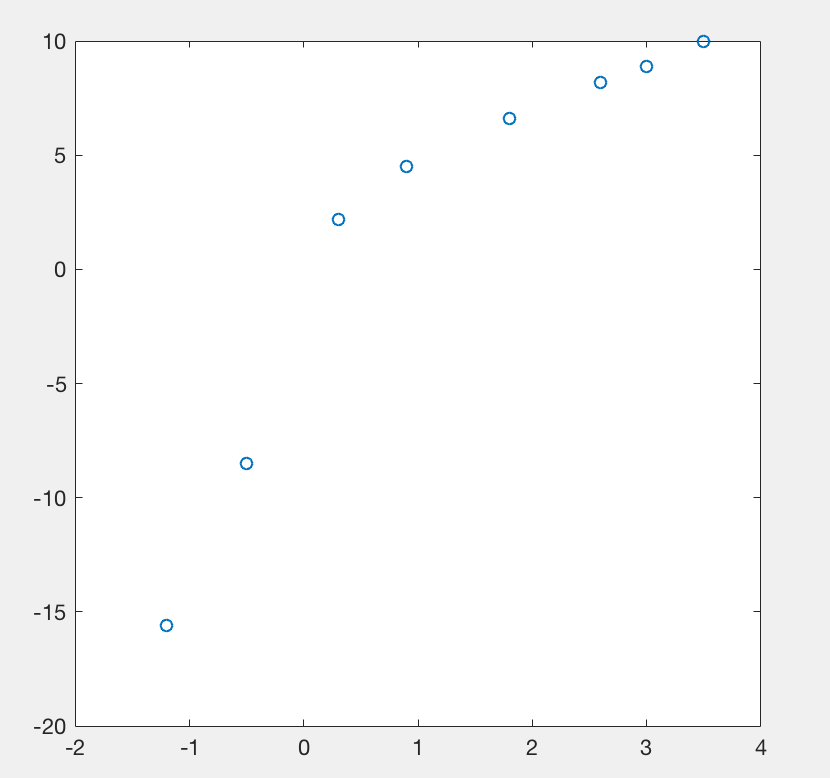
2.scatter(x,y) 在向量 x 和 y 指定的位置创建一个包含圆形的散点图。该类型的图形也称为气泡图。

corrcoef(x,y) -1<=r<=1 相关系数

 

% 第一个1是x与y的相关系数,左边第一个0.9202是x与y相关系数,第二个0.9202是y与x相关系数,第二个1是y与y的相关系数

>> x=[-1.2 -0.5 0.3 0.9 1.8 2.6 3.0 3.5];
y=[-15.6 -8.5 2.2 4.5 6.6 8.2 8.9 10.0];
>> scatter(x,y);
>> box on 
>> axis square
>> corrcoef(x,y)

ans =

    1.0000    0.9202
    0.9202    1.0000

 

 

 

 

>> x=[-1.2 -0.5 0.3 0.9 1.8 2.6 3.0 3.5];
y=[-15.6 -8.5 2.2 4.5 6.6 8.2 8.9 10.0];
figure
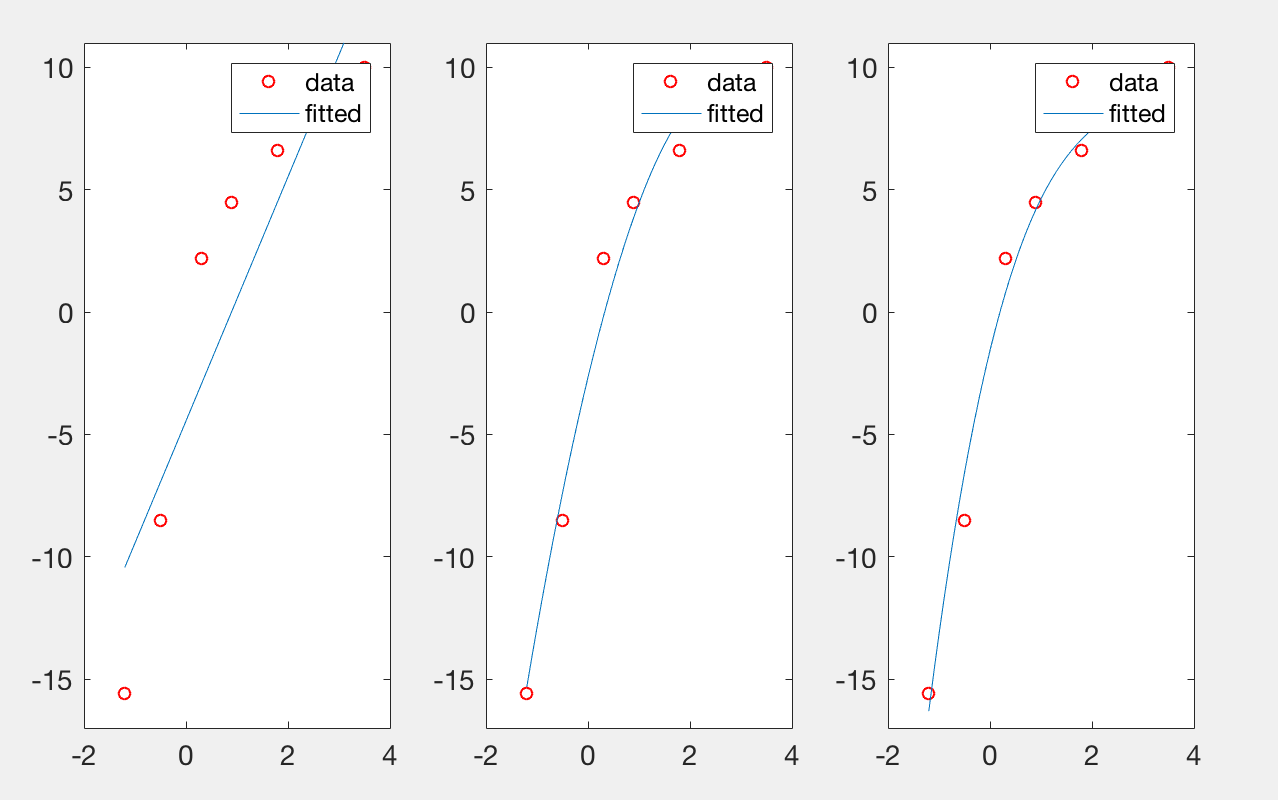
for i=1:3
subplot(1,3,i);p=polyfit(x,y,i);%i代表最高次数
xfit=x(1):0.1:x(end);
yfit=polyval(p,xfit);
plot(x,y,'ro',xfit,yfit);
set(gca,'fontsize',14)
ylim([-17 11]);
legend('data','fitted');
end

 

 

 

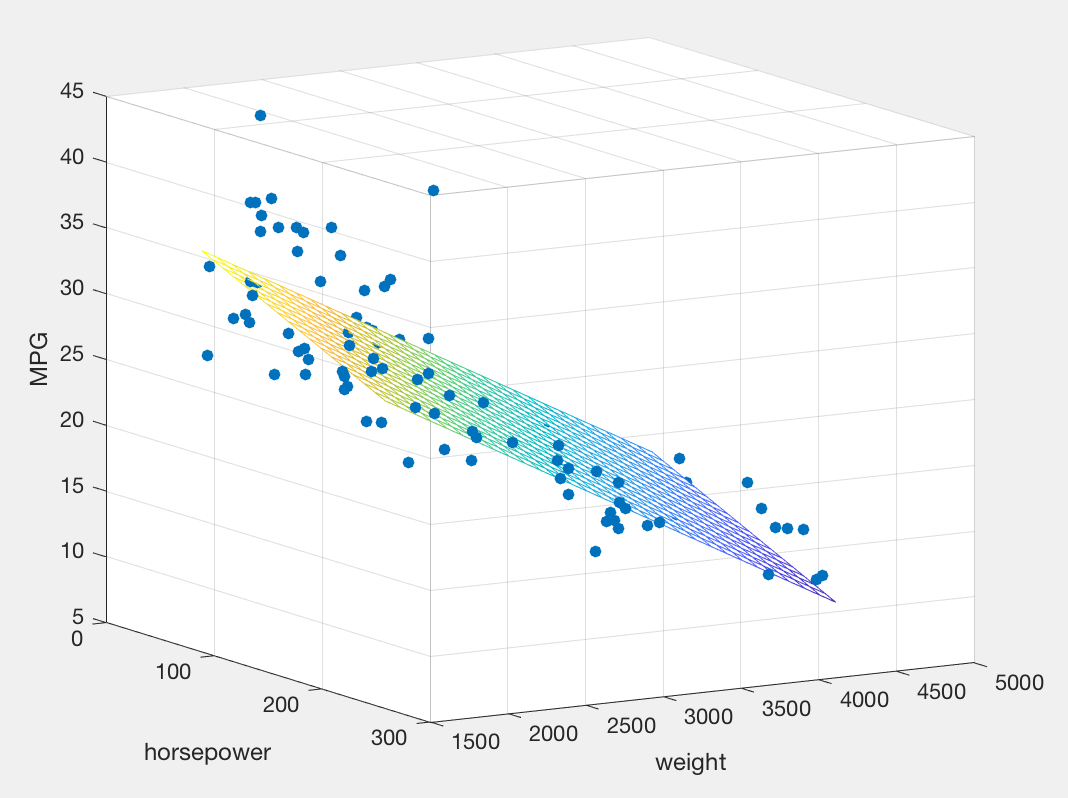
load carsmall;
y=MPG;
x1=Weight;x2=Horsepower;
x=[ones(length(x1),1) x1 x2];%矩阵1*3里有3个参数 常数 m*1列向量 m为x1系数的长度
b=regress(y,x);%regress用最小二乘法求出系数
x1fit=min(x1):100:max(x1);
x2fit=min(x2):10:max(x2);
[X1,X2]=meshgrid(x1fit,x2fit);
YFIT=b(1)+b(2)*X1+b(3)*X2;
scatter3(x1,x2,y,'fitted');hold on;
mesh(X1,X2,YFIT);hold off;
xlabel('weight');
ylabel('horsepower');
zlabel('MPG');
view(50,10);

 

 

 

对于非线性拟合，可以用cftool()

>> cftool

 

 

内插

一维的如下，还有二维的这里暂先不做介绍

interp1() Linear Interpolation

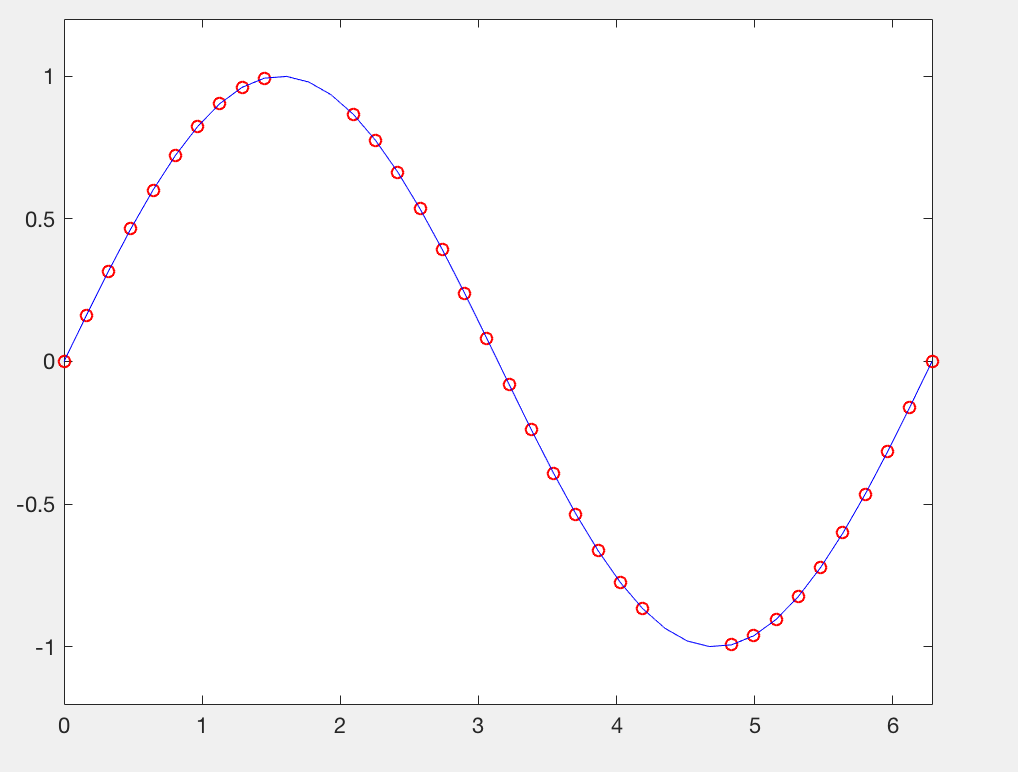
x=linspace(0,2*pi,40);%linspace用于产生指定范围内的指定数量点数，相邻数据跨度相同，并返回一个行向量
x_m=x;
x_m([11:13,28:30])=NaN;
y_m=sin(x_m);
plot(x_m,y_m,'ro');
xlim([0,2*pi]);ylim([-1.2,1.2]);
m_i=~isnan(x_m);%取出数字的部分
y_i=interp1(x_m(m_i),y_m(m_i),x);
hold on
plot(x,y_i,'-b');
hold off

 

 

pchip()

spline()三次样条函数插值

x=linspace(0,2*pi,40);%linspace用于产生指定范围内的指定数量点数，相邻数据跨度相同，并返回一个行向量
x_m=x;
x_m([11:13,28:30])=NaN;
y_m=sin(x_m);
plot(x_m,y_m,'ro');
xlim([0,2*pi]);ylim([-1.2,1.2]);
m_i=~isnan(x_m);%取出数字的部分
y_i=spline(x_m(m_i),y_m(m_i),x);
hold on
plot(x,y_i,'-b');
hold off

 

 

x=-3:3;
y=[-1 -1 -1 0 1 1 1];
t=-3:0.01:3;
s=spline(x,y,t);
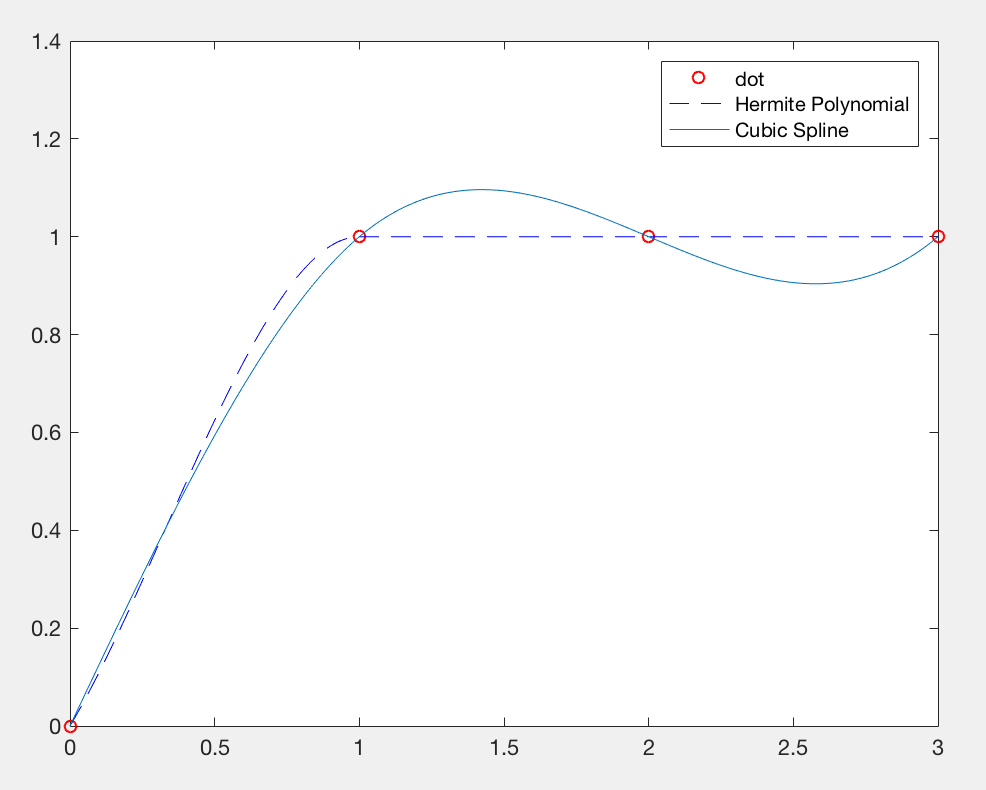
p=pchip(x,y,t);%Hermite Polynomial 
plot(x,y,'ro');
hold on
plot(t,p,'--b');
plot(t,s,'-');
set(gca,'ylim',[0 1.4]);
legend('dot','Hermite Polynomial','Cubic Spline');
hold off