遗传算法解TSP问题
function fitness
CityNum=30;%U can choose 10 30 50
[dislist,Clist]=tsp(CityNum);
inn=30;%初始种群大小
gnmax=500;%最大代数
pc=0.8;%交叉概率
pm=0.5;%变异概率
%产生初始种群
s=zeros(inn,CityNum);
%生成inn*inn大的矩阵
for i=1:inn
s(i,:)=randperm(CityNum);%将一列序号随机打乱,序号必须是整数。
end
[~,p]=objf(s,dislist);
gn=1;
ymean=zeros(gn,1);
ymax=zeros(gn,1);
xmax=zeros(inn,CityNum);
scnew=zeros(inn,CityNum);
smnew=zeros(inn,CityNum);
while gn<gnmax+1
for j=1:2:inn
seln=sel(p);%选择操作
scro=cro(s,seln,pc);%交叉操作 pc=0.8
scnew(j,:)=scro(1,:);
scnew(j+1,:)=scro(2,:);
smnew(j,:)=mut(scnew(j,:),pm);%变异操作
smnew(j+1,:)=mut(scnew(j+1,:),pm);
end
s=smnew;%产生了新的种群
[f,p]=objf(s,dislist);%计算新种群的适应度
%记录当前代最好和平均的适应度
%[Y,U]=max(A):返回行向量Y和U,Y向量记录A的每列的最大值,U向量记录每列最大值的行号。
[fmax,nmax]=max(f);%nmax代表f取最大时的index,fmax代表f的最大值
ymean(gn)=1000/mean(f);%ymean平均适应度
ymax(gn)=1000/fmax;%ymax最大适应度
%记录当前代的最佳个体
x=s(nmax,:);
xmax(gn,:)=x;
drawTSP(Clist,x,ymax(gn),gn,0);
gn=gn+1;
end
[min_ymax,index]=min(ymax);
drawTSP(Clist,xmax(index,:),min_ymax,index,1);
figure(2);
plot(ymax,'r');
hold on;
plot(ymean,'b');grid;
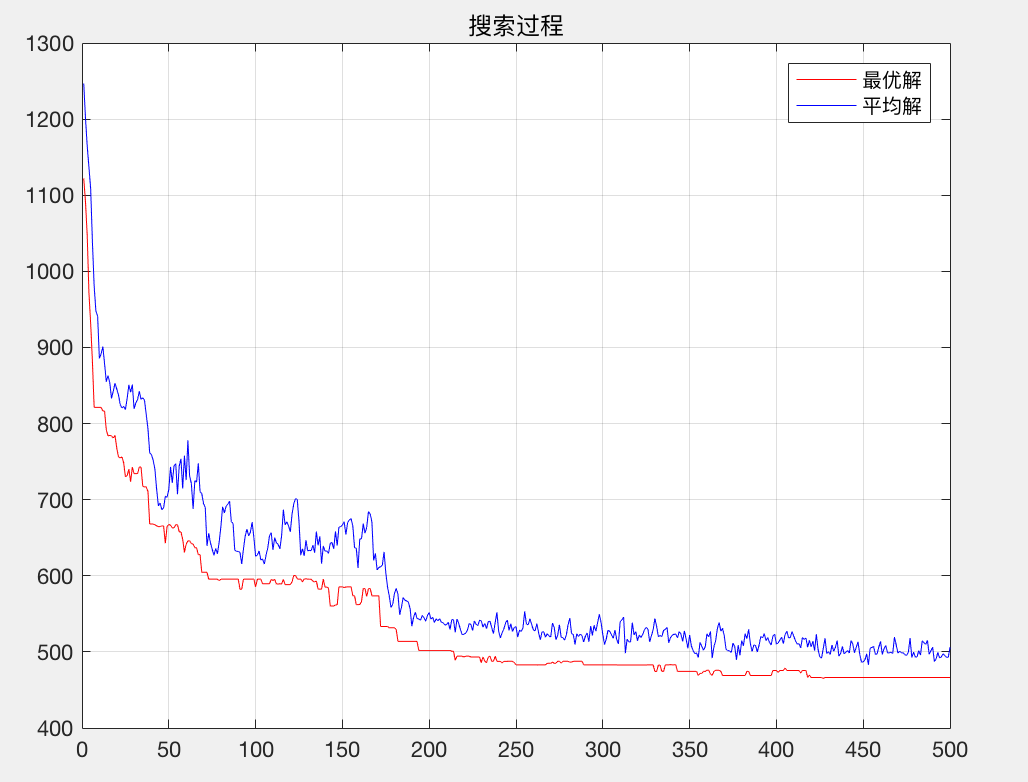
title('搜索过程');
legend('最优解','平均解');
%最优解
fprintf('遗传算法得到的最短距离:%.2f\n',min_ymax);
fprintf('遗传算法得到的最短路线');
disp(xmax(index,:));
end
%计算所有种群的适应度
function [f,p]=objf(s,dislist)
inn=size(s,1); %读取种群大小
f=zeros(inn,1);
for i=1:inn
f(i)=CalDist(dislist,s(i,:)); %计算函数值,即适应度
end
f=1000./f'; %取距离倒数
%根据个体的适应度计算其被选择的概率
fsum=0;
for i=1:inn
fsum=fsum+f(i)^15;% 让适应度越好的个体被选择概率越高
end
ps=zeros(inn,1);
for i=1:inn
ps(i)=f(i)^15/fsum;
end
%计算累积概率
p=zeros(inn,1);
p(1)=ps(1);
for i=2:inn
p(i)=p(i-1)+ps(i);
end
p=p';
end
%判断变异
function pcc=pro(pc)
test(1:100)=0;
l=round(100*pc);
test(1:l)=1;
n=round(99*rand)+1;
pcc=test(n);
end
function seln=sel(p)
seln=zeros(2,1);
for i=1:2
r=rand;
prand=p-r;
j=1;
while prand(j)<0
j=j+1;
end
seln(i)=j;
while i==2&&j==seln(i-1)%如果相同就再选一次
r=rand;
prand=p-r;
j=1;
while prand(j)<0
j=j+1;
end
end
end
end
%“交叉”操作
function scro=cro(s,seln,pc)
bn=size(s,2);
pcc=pro(pc); %根据交叉概率决定是否进行交叉操作,1则是,0则否
scro(1,:)=s(seln(1),:);
scro(2,:)=s(seln(2),:);
if pcc==1
c1=round(rand*(bn-2))+1; %在[1,bn-1]范围内随机产生一个交叉位
c2=round(rand*(bn-2))+1;
chb1=min(c1,c2);
chb2=max(c1,c2);
middle=scro(1,chb1+1:chb2);
scro(1,chb1+1:chb2)=scro(2,chb1+1:chb2);
scro(2,chb1+1:chb2)=middle;
for i=1:chb1 %似乎有问题
while find(scro(1,chb1+1:chb2)==scro(1,i))
zhi=find(scro(1,chb1+1:chb2)==scro(1,i));
y=scro(2,chb1+zhi);
scro(1,i)=y;
end
while find(scro(2,chb1+1:chb2)==scro(2,i))
zhi=find(scro(2,chb1+1:chb2)==scro(2,i));
y=scro(1,chb1+zhi);
scro(2,i)=y;
end
end
for i=chb2+1:bn
while find(scro(1,1:chb2)==scro(1,i))
zhi=logical(scro(1,1:chb2)==scro(1,i));
y=scro(2,zhi);
scro(1,i)=y;
end
while find(scro(2,1:chb2)==scro(2,i))
zhi=logical(scro(2,1:chb2)==scro(2,i));
y=scro(1,zhi);
scro(2,i)=y;
end
end
end
end
%变异操作
function snnew=mut(snew,pm)
bn=size(snew,2);
snnew=snew;
%判断是否变异
%test(1:100)=0;
%l=round(100*pc);
%test(1:l)=1;
%n=round(99*rand)+1;
%pmm=test(n);
pmm=pro(pm);
if pmm==1
c1=round(rand*(bn-2))+1;%产生一个[1,bn-1]的数
c2=round(rand*(bn-2))+1;
chb1=min(c1,c2);
chb2=max(c1,c2);
x=snew(chb1+1:chb2);
snnew(chb1+1:chb2)=fliplr(x);%将矩阵中的数左右对换
end
end
%城市位置坐标
function [DLn,cityn]=tsp(n)
DLn=zeros(n,n);
if n==10
city10=[0.4 0.4439;0.2439 0.1463;0.1707 0.2293;0.2293 0.761;0.5171 0.9414;
0.8732 0.6536;0.6878 0.5219;0.8488 0.3609;0.6683 0.2536;0.6195 0.2634];%10 cities d'=2.691
for i=1:10
for j=1:10
DLn(i,j)=((city10(i,1)-city10(j,1))^2+(city10(i,2)-city10(j,2))^2)^0.5;
end
end
cityn=city10;
end
if n==30
city30=[41 94;37 84;54 67;25 62;7 64;2 99;68 58;71 44;54 62;83 69;64 60;18 54;22 60;
83 46;91 38;25 38;24 42;58 69;71 71;74 78;87 76;18 40;13 40;82 7;62 32;58 35;45 21;41 26;44 35;4 50];%30 cities d'=423.741 by D B Fogel
for i=1:30
for j=1:30
DLn(i,j)=((city30(i,1)-city30(j,1))^2+(city30(i,2)-city30(j,2))^2)^0.5;
end
end
cityn=city30;
end
if n==50
city50=[31 32;32 39;40 30;37 69;27 68;37 52;38 46;31 62;30 48;21 47;25 55;16 57;
17 63;42 41;17 33;25 32;5 64;8 52;12 42;7 38;5 25; 10 77;45 35;42 57;32 22;
27 23;56 37;52 41;49 49;58 48;57 58;39 10;46 10;59 15;51 21;48 28;52 33;
58 27;61 33;62 63;20 26;5 6;13 13;21 10;30 15;36 16;62 42;63 69;52 64;43 67];%50 cities d'=427.855 by D B Fogel
for i=1:50
for j=1:50
DLn(i,j)=((city50(i,1)-city50(j,1))^2+(city50(i,2)-city50(j,2))^2)^0.5;
end
end
cityn=city50;
end
end
%适应度函数
function F=CalDist(dislist,s)
%传入参数 距离表 种群
%传出参数 城市间的距离总和
Dis=0;
n=size(s,2);
for i=1:(n-1)
Dis=Dis+dislist(s(i),s(i+1));
end
Dis=Dis+dislist(s(1),s(n));
F=Dis;
end
function drawTSP(Clist,BSF,bsf,p,f)
CityNum=size(Clist,1);
for i=1:CityNum-1
plot([Clist(BSF(i),1),Clist(BSF(i+1),1)],[Clist(BSF(i),2),Clist(BSF(i+1),2)],'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g');
text(Clist(BSF(i),1),Clist(BSF(i),2),[' ',int2str(BSF(i))]);
text(Clist(BSF(i+1),1),Clist(BSF(i+1),2),[' ',int2str(BSF(i+1))]);
hold on;
end
plot([Clist(BSF(CityNum),1),Clist(BSF(1),1)],[Clist(BSF(CityNum),2),Clist(BSF(1),2)],'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g');
title([num2str(CityNum),'城市TSP']);
if f==0&&CityNum~=10
text(5,5,['第 ',int2str(p),' 代',' 最短距离为 ',num2str(bsf)]);
else
text(5,5,['最终搜索结果:最短距离 ',num2str(bsf),', 在第 ',num2str(p),' 代达到']);
end
if CityNum==10
if f==0
text(0,0,['第 ',int2str(p),' 代',' 最短距离为 ',num2str(bsf)]);
else
text(0,0,['最终搜索结果:最短距离 ',num2str(bsf),', 在第 ',num2str(p),' 代达到']);
end
end
hold off;
pause(0.05);
end
不明白:对于变异概率和交叉概率取什么值才能 取到 最小值 (开学后去问老师吧~~!)