POJ 2018 Best Cow Fences

斜率优化。

设$s[i]$表示前缀和，$avg(i,j)=(s[j]-s[i-1])/(j-(i-1))$。就是$(j,s[j])$与$(i-1,s[i-1])$两点之间的斜率。

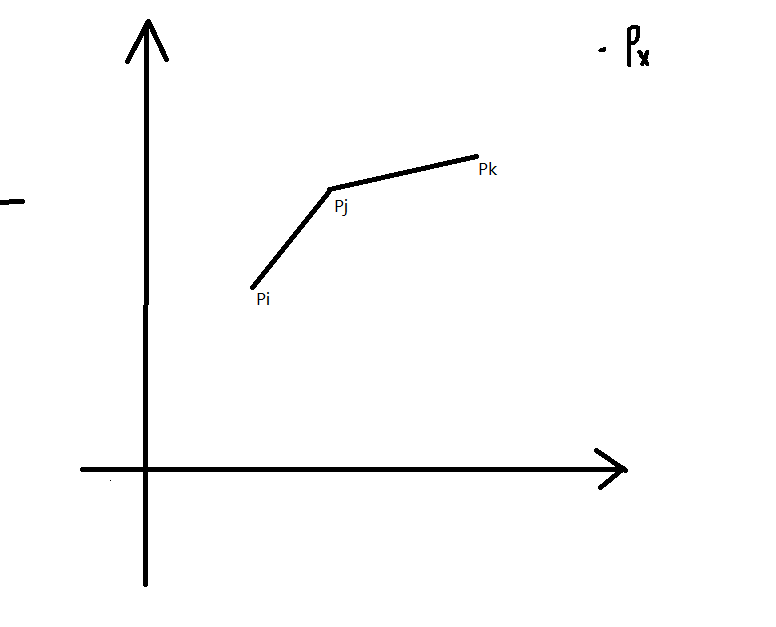
如果，我们目前在计算$px$与哪个点相连斜率最大，那么一定不会是$pj$点。因为不是$pi$比优就是$pk$比$pi$优。因此斜率优化可以将$pj$这样的点直接删除。

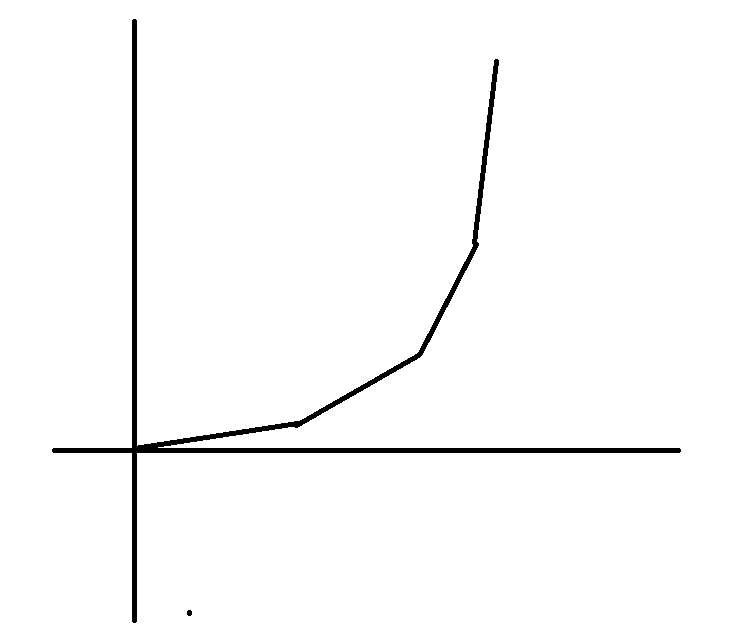
因此队列里存着的相邻两点的斜率是不断增大的。

因为$(s[i+1]-s[i])/1$是大于等于$1$的，所以如果$pi$点与$pt$点形成的斜率最大，那么与$pi+1$点形成最大斜率的点肯定大于等于$pt$点。

根据这一点，每一个点入队一次出队一次，时间复杂度$O(n)$。

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<ctime>
#include<iostream>
using namespace std;
typedef long long LL;
const double pi=acos(-1.0),eps=1e-10;
void File()
{
    freopen("D:\\in.txt","r",stdin);
    freopen("D:\\out.txt","w",stdout);
}
template <class T>
inline void read(T &x)
{
    char c = getchar();
    x = 0;
    while(!isdigit(c)) c = getchar();
    while(isdigit(c))
    {
        x = x * 10 + c - '0';
        c = getchar();
    }
}

int n,k;
double a[100010],s[100010];
int q[100010],f1,f2;

bool delete1(int a,int b,int c)
{
    if((s[c]-s[a])*(c-b)<(s[c]-s[b])*(c-a)) return 1;
    return 0;
}

bool delete2(int a,int b,int c)
{
    if((s[c]-s[b])*(b-a)<(s[b]-s[a])*(c-b)) return 1;
    return 0;
}

int main()
{
    while(~scanf("%d%d",&n,&k))
    {
        for(int i=1;i<=n;i++) scanf("%lf",&a[i]);
        for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];

        f1=0; f2=0; q[f2]=0; double ans=0;
        for(int i=k;i<=n;i++)
        {
            while(1)
            {
                if(f2-f1+1<2) break;
                if(delete1(q[f1],q[f1+1],i)) f1++;
                else break;
            }

            ans=max(ans,1.0*(s[i]-s[q[f1]])/(i-q[f1]));

            while(1)
            {
                if(f2-f1+1<2) break;
                if(delete2(q[f2-1],q[f2],i-k+1)) f2--;
                else break;
            }

            f2++; q[f2]=i-k+1;

        }
        printf("%d\n",(int)(1000*ans));
    }
    return 0;
}