CSU 1810 Reverse

湖南省第十二届大学生计算机程序设计竞赛$H$题

规律，递推。

这种问题一看就有规律。可以按位统计对答案的贡献。即第$1$位对答案作出了多少贡献，第$2$位对答案作出了多少贡献.....累加和就是答案。

先写一个暴力的程序来找找规律：

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<iostream>
using namespace std;
typedef long long LL;
const double pi=acos(-1.0),eps=1e-6;
void File()
{
    freopen("D:\\in.txt","r",stdin);
    freopen("D:\\out.txt","w",stdout);
}
template <class T>
inline void read(T &x)
{
    char c = getchar();
    x = 0;
    while(!isdigit(c)) c = getchar();
    while(isdigit(c))
    {
        x = x * 10 + c - '0';
        c = getchar();
    }
}

const int maxn=1010;
struct X
{
    int p;
}s[maxn];
int n;
int f[maxn][maxn];

int main()
{
    while(~scanf("%d",&n))
    {
        memset(f,0,sizeof f);
        for(int i=1;i<=n;i++) s[i].p=i;

        for(int i=1;i<=n;i++)
        {
            for(int j=i;j<=n;j++)
            {
                for(int k=i;k<=(i+j)/2;k++) swap(s[k],s[j-(k-i)]);

                for(int k=1;k<=n;k++) f[s[k].p][k]++;

                for(int k=i;k<=(i+j)/2;k++) swap(s[k],s[j-(k-i)]);
            }
        }

        for(int i=1;i<=n;i++)
        {
            int sum=0;
            for(int j=1;j<=n;j++)
            {
               // sum=sum+(int)pow(10.0,j-1)*f[i][j];
                printf("%3d ",f[i][j]);
            }
            printf("\n");
          //  printf("%d ",sum);
        }
        printf("\n");

    }
    return 0;
}

上面的代码中，$f[i][j]$表示$i$这一位，所有交换中，在$j$位出现了几次；答案就是$\sum\limits_{i = 1}^n {\left( {s[i]×\left( {\sum\limits_{j = 1}^n {f[i][j]×{{10}^{j - 1}}} } \right)} \right)} $。

输出来看一下$n=10$和$n=11$时候的情况，看看$f[i][j]$有没有什么规律：

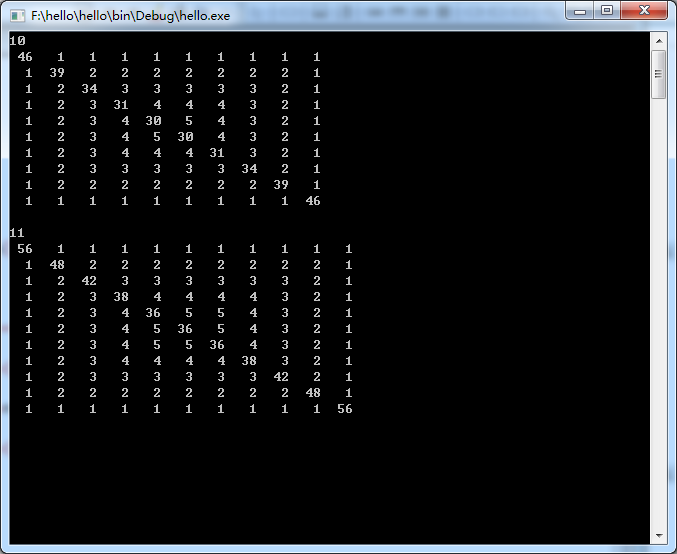
通过观察可以发现：

$[1].$每一行的和都是一样的，$n=x$时，每一行的和$cnt[x]$都是一样的，并且$cnt[x]=x+cnt[x-1]$。

$[2].$第$i$行的贡献${\sum\limits_{j = 1}^n {f[i][j]×{{10}^{j - 1}}} }$可以由第$i-1$行的贡献${\sum\limits_{j = 1}^n {f[i-1][j]×{{10}^{j - 1}}} }$递推而来。

也就是说，我们可以$O(n)$效率得到每一位的贡献，然后乘上输入的那个权值就是答案了。

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<iostream>
using namespace std;
typedef long long LL;
const double pi = acos(-1.0), eps = 1e-8;
void File()
{
    freopen("D:\\in.txt", "r", stdin);
    freopen("D:\\out.txt", "w", stdout);
}
template <class T>
inline void read(T &x)
{
    char c = getchar(); x = 0; while (!isdigit(c)) c = getchar();
    while (isdigit(c)) { x = x * 10 + c - '0'; c = getchar(); }
}

const LL mod = 1e9 + 7;
const int maxn = 100010;
LL a[maxn], cnt[maxn], POW[maxn], sPOW[maxn], num[maxn];
char s[maxn];
int n;

int main()
{
    cnt[1] = 1; 
    for (int i = 2; i <= 100000; i++) cnt[i] = (cnt[i - 1] + i) % mod;
    POW[0] = 1; sPOW[0] = 1;
    for (int i = 1; i <= 100000; i++)
    {
        POW[i] = (LL)10 * POW[i - 1] % mod;
        sPOW[i] = (sPOW[i - 1] + POW[i]) % mod;
    }

    while (~scanf("%d%s", &n, s))
    {
        memset(num, 0, sizeof num);
        memset(a, 0, sizeof a);

        num[0] = (cnt[n] - (n - 1) + mod) % mod;
        a[0] = (num[0]*POW[0] % mod + (sPOW[n - 1] - sPOW[0] + mod) % mod) % mod;
        

        int L = 1, R = n - 1;
        for (int i = 1; i < n / 2; i++)
        {
            L++, R--; num[i] = (num[i - 1] - (R - L + 1) + mod) % mod;
            a[i] = (a[i - 1] + sPOW[R] - sPOW[L - 1] + mod) % mod;
            a[i] = (a[i] + ((num[i] - i + mod) % mod)*POW[i] % mod) % mod;
            a[i] = (a[i] - (((num[i - 1] - i + mod) % mod)*POW[i - 1] % mod) + mod) % mod;
        }
        
        num[n - 1] = num[0];
        a[n - 1] = (num[n - 1] * POW[n - 1] % mod + sPOW[n - 2]) % mod;

        L = 0, R = n - 2; LL d = 1;
        for (int i = n - 2; i >= (n ) / 2; i--)
        {
            L++, R--; num[i]= (num[i + 1] - (R - L + 1) + mod) % mod;
            a[i]= (a[i + 1] + sPOW[R] - sPOW[L - 1] + mod) % mod;
            a[i] = (a[i] + ((num[i] - d + mod) % mod)*POW[i] % mod) % mod;
            a[i] = (a[i] - (((num[i + 1] - d + mod) % mod)*POW[i + 1] % mod) + mod) % mod;
            d++;
        }

        LL ans = 0;
        for (int i = 0; s[i]; i++) ans = (ans + (LL)(s[i] - '0')*a[n-i-1] % mod) % mod;
        cout << ans << endl;
    }
    return 0;
}