HDU 5863 cjj's string game
$dp$,矩阵加速。
设$dp[i][j][0]$表示:长度为$i$的两个字符串,之前还未出现过长度为$m$相同的,目前为止最后$j$个是相同的。
设$dp[i][j][1]$表示:长度为$i$的两个字符串,之前已经出现过长度为$m$相同的,目前为止最后$j$个是相同的。
递推式很容易写,$n$有点大,矩阵加速。下图以$m=4$为例构造矩阵。
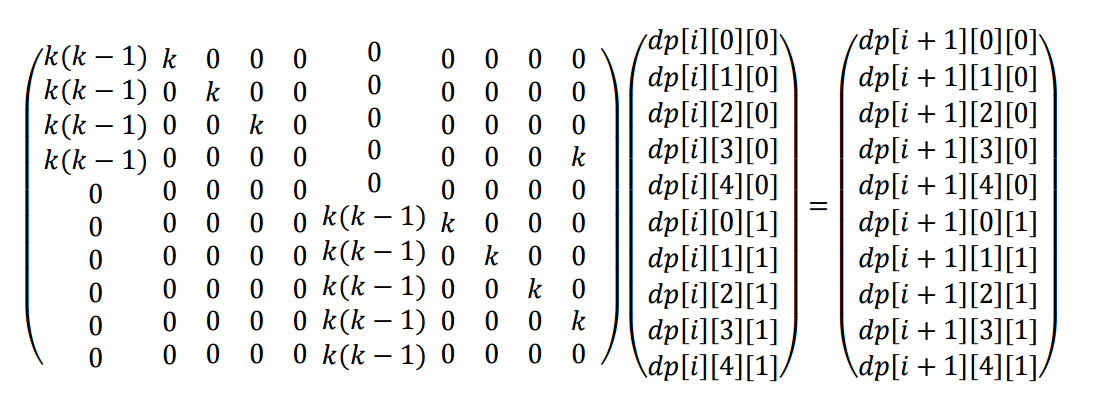
#pragma comment(linker, "/STACK:1024000000,1024000000") #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #include<vector> #include<map> #include<set> #include<queue> #include<stack> #include<iostream> using namespace std; typedef long long LL; const double pi=acos(-1.0),eps=1e-8; void File() { freopen("D:\\in.txt","r",stdin); freopen("D:\\out.txt","w",stdout); } template <class T> inline void read(T &x) { char c = getchar(); x = 0;while(!isdigit(c)) c = getchar(); while(isdigit(c)) { x = x * 10 + c - '0'; c = getchar(); } } LL n,MOD=1000000007; int T,m,k; struct Matrix { long long A[25][25]; int R, C; Matrix operator*(Matrix b); }; Matrix X, Y, Z; Matrix cheng(Matrix a,Matrix b) { Matrix c; int i, j, k; for (i = 1; i <= a.R; i++) for (j = 1; j <= b.C; j++){ c.A[i][j]=0; for (k = 1; k <= a.C; k++) c.A[i][j] = (c.A[i][j] + (a.A[i][k] * b.A[k][j]) % MOD) % MOD; } c.R = a.R; c.C = b.C; return c; } void init() { memset(X.A, 0, sizeof X.A); memset(Y.A, 0, sizeof Y.A); memset(Z.A, 0, sizeof Z.A); Y.R = 2*(m+1); Y.C = 2*(m+1); for (int i = 1; i <= 2*(m+1); i++) Y.A[i][i] = 1; X.R = 2*(m+1); X.C = 2*(m+1); for(int i=1;i<=m;i++) X.A[i][1]=k*(k-1); for(int i=1;i<=m-1;i++) X.A[i][i+1]=k; for(int i=m+2;i<=2*m+2;i++) X.A[i][m+2]=k*(k-1); for(int i=m+2;i<=2*m+1;i++) X.A[i][i+1]=k; X.A[m][2*m+2]=k; Z.R = 1; Z.C = 2*(m+1); Z.A[1][1]=1; } void work() { while (n) { if (n % 2 == 1) Y = cheng(Y,X); n = n >> 1; X = cheng(X,X); } Z = cheng(Z,Y); LL ans=0; for(int i=m+2;i<=2*(m+1);i++) ans=(ans+Z.A[1][i])%MOD; printf("%lld\n",ans); } int main() { scanf("%d",&T); while(T--) { scanf("%lld%d%d",&n,&m,&k); init(); work(); } return 0; }


