HDU 5829 Rikka with Subset

快速数论变换ntt。

早上才刚刚接触了一下FFT，然后就开始撸这题了，所以要详细地记录一下。

看了这篇巨巨的博客才慢慢领会的：http://blog.csdn.net/cqu_hyx/article/details/52194696

FFT的作用是计算卷积。可以简单的理解为计算多项式*多项式最后得到的多项式，暴力计算是O(n*n)的，FFT可以做到O(nlogn)。

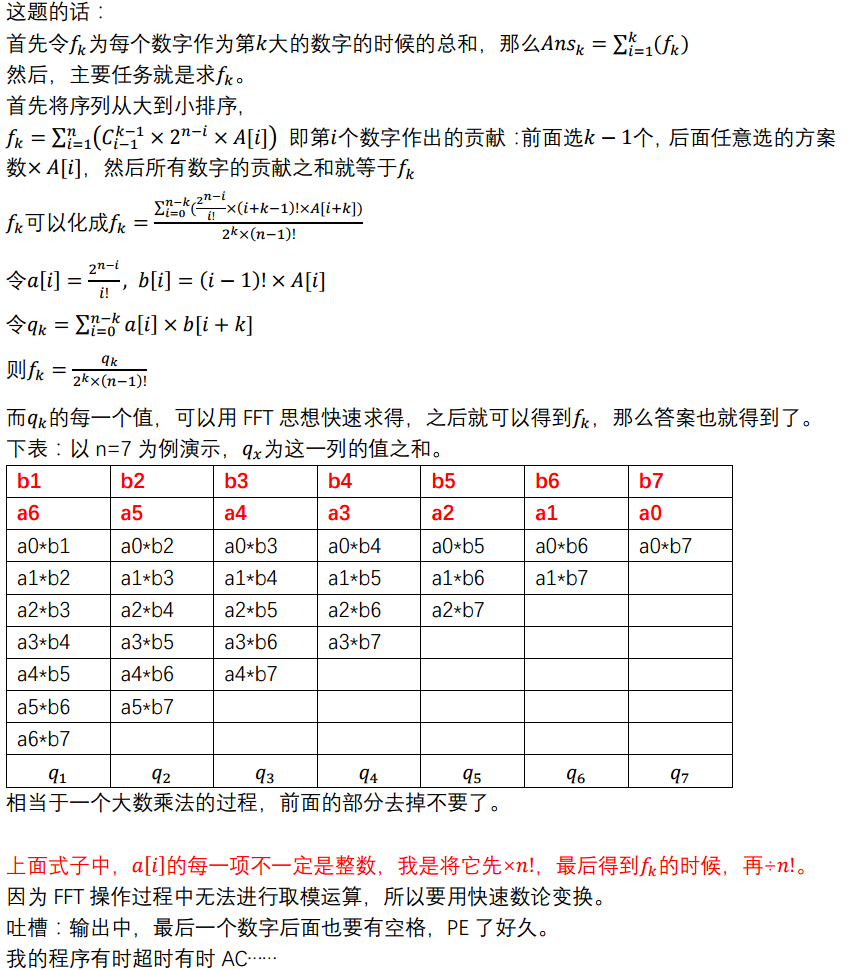
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<iostream>
using namespace std;
typedef long long LL;
const double pi=acos(-1.0),eps=1e-8;
void File()
{
    freopen("D:\\in.txt","r",stdin);
    freopen("D:\\out.txt","w",stdout);
}
template <class T>
inline void read(T &x)
{
    char c = getchar(); x = 0;while(!isdigit(c)) c = getchar();
    while(isdigit(c)) { x = x * 10 + c - '0'; c = getchar();  }
}

const int maxn=300005;
const LL mod=998244353;
const LL G=3;

LL t[maxn],a[maxn],b[maxn],c[maxn],f[maxn],fac[maxn],NI[maxn];
int T,n,m;
LL rev[maxn],N,len,inv;

LL POW[maxn],NiPOW[maxn];

LL power(LL x,LL y)
{
    LL res=1;
    for(;y;y>>=1,x=(x*x)%mod)
    {
        if(y&1)res=(res*x)%mod;
    }
    return res;
}

void init()
{
    while((n+m)>=(1<<len))len++;
    N=(1<<len);
    inv=power(N,mod-2);
    for(int i=0;i<N;i++)
    {
        LL pos=0;
        LL temp=i;
        for(int j=1;j<=len;j++)
        {
            pos<<=1;pos |= temp&1;temp>>=1;
        }
        rev[i]=pos;
    }
}

void ntt(LL *a,LL n,LL re)
{
    for(int i=0;i<n;i++)
    {
        if(rev[i]>i)
        {
            swap(a[i],a[rev[i]]);
        }
    }
    for(int i=2;i<=n;i<<=1)
    {
        int mid=i>>1;

        LL wn=power(G,(mod-1)/i);
        if(re) wn=power(wn,(mod-2));
        for(int j=0;j<n;j+=i)
        {
            LL w=1;
            for(int k=0;k<mid;k++)
            {
                int temp1=a[j+k];
                int temp2=(LL)a[j+k+mid]*w%mod;
                a[j+k]=(temp1+temp2);if(a[j+k]>=mod)a[j+k]-=mod;
                a[j+k+mid]=(temp1-temp2);if(a[j+k+mid]<0)a[j+k+mid]+=mod;
                w=(LL)w*wn%mod;
            }
        }
    }
    if(re)
    {
        for(int i=0;i<n;i++)
        {
            a[i]=(LL)a[i]*inv%mod;
        }
    }
}

bool cmp(LL a,LL b) {return a>b;}

LL extend_gcd(LL a,LL b,LL &x,LL &y)
{
    if(a==0&&b==0) return -1;
    if(b==0){x=1;y=0;return a;}
    LL d=extend_gcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}

LL mod_reverse(LL a,LL n)
{
    LL x,y;
    LL d=extend_gcd(a,n,x,y);
    if(d==1) return (x%n+n)%n;
    else return -1;
}

int main()
{
    fac[0]=1; for(int i=1;i<=100000;i++) fac[i]=(LL)i*fac[i-1]%mod;
    for(int i=0;i<=100000;i++) NI[i]=mod_reverse(fac[i],mod);
    POW[0]=1; for(int i=1;i<=100000;i++) POW[i]=(LL)2*POW[i-1]%mod;
    for(int i=0;i<=100000;i++) NiPOW[i]=mod_reverse(POW[i],mod);

    scanf("%d",&T); while(T--)
    {
        len=0;  memset(c,0,sizeof c); memset(a,0,sizeof a); memset(b,0,sizeof b);

        scanf("%d",&n); m=n;
        for(int i=1;i<=n;i++) { int x; scanf("%d",&x); t[i]=(LL)x; }

        sort(t+1,t+1+n,cmp);
        for(int i=0;i<n;i++)
        {
            LL x=fac[n]*NI[i]%mod;
            a[i]=x*POW[n-i]%mod;
        }
        for(int i=1;i<=n;i++) b[n-i]=t[i]*fac[i-1]%mod;

        init(); ntt(a,N,0); ntt(b,N,0);
        for(int i=0;i<=N;i++) c[i]=a[i]*b[i]%mod;
        ntt(c,N,1);

        for(int i=0;i<n;i++) f[n-i]=c[i]*NI[n]%mod;
        for(int i=1;i<=n;i++) f[i]=f[i]*NI[i-1]%mod;
        for(int i=1;i<=n;i++) f[i]=f[i]*NiPOW[i]%mod;
        LL ans=0; for(int i=1;i<=n;i++) { ans=(ans+f[i])%mod; printf("%lld ",ans); }
        printf("\n");
    }
    return 0;
}