UVA 11551 Experienced Endeavour
矩阵快速幂。
题意事实上已经告诉我们这是一个矩阵乘法的运算过程。
构造矩阵:把xi列的bij都标为1.
例如样例二:
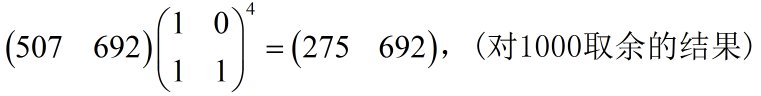
#include<cstdio> #include<cstring> #include<cmath> #include<vector> #include<algorithm> using namespace std; long long const MOD = 1000; int n, m; long long a[50 + 5]; struct Matrix { long long A[50 + 5][50 + 5]; int R, C; Matrix operator*(Matrix b); }; Matrix X, Y, Z; Matrix Matrix::operator*(Matrix b) { Matrix c; memset(c.A, 0, sizeof(c.A)); int i, j, k; for (i = 1; i <= R; i++) for (j = 1; j <= b.C; j++) for (k = 1; k <= C; k++) c.A[i][j] = (c.A[i][j] + (A[i][k] * b.A[k][j]) % MOD) % MOD; c.R = R; c.C = b.C; return c; } void init() { memset(X.A, 0, sizeof X.A); memset(Y.A, 0, sizeof Y.A); memset(Z.A, 0, sizeof Z.A); Y.R = n; Y.C = n; for (int i = 1; i <= n; i++) Y.A[i][i] = 1; X.R = n; X.C = n; for (int j = 1; j <= n; j++) { int xi; scanf("%d", &xi); for (int i = 1; i <= xi; i++) { int num; scanf("%d", &num); num++; X.A[num][j] = 1; } } Z.R = 1; Z.C = n; for (int i = 1; i <= n; i++) Z.A[1][i] = a[i]; } void read() { scanf("%d%d", &n, &m); for (int i = 1; i <= n; i++) { scanf("%lld", &a[i]); a[i] = a[i] % MOD; } } void work() { while (m) { if (m % 2 == 1) Y = Y*X; m = m >> 1; X = X*X; } Z = Z*Y; for (int i = 1; i <= n; i++) { printf("%lld", Z.A[1][i]); if (i<n) printf(" "); else printf("\n"); } } int main() { int T; scanf("%d", &T); while (T--) { read(); init(); work(); } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号