HUST 1351 Group
(莫名其妙的被一个叫布布扣的网站收录了......什么鬼)
简单DP。dp[i][j]表示把前i个数字分成j段的最优解,
递推式很容易写: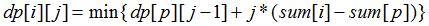
(其中sum[]是前缀和;p <= i - L,并且前p个数能分成j-1段,下文不再说明p的范围,都是一样的)
得到递推式之后暴力DP的话复杂度为o(n*n*k),显然超时。
递推式可以变形成这样: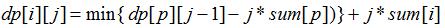
现在,想求得dp[i][j],只需求得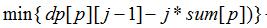 ,即前面所有P的位置的最小值。
,即前面所有P的位置的最小值。
然而,上面这式子可以递推得到:
令f[i][j]=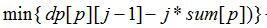 ,
,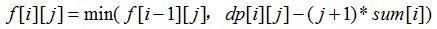
最终,得到了两个式子:
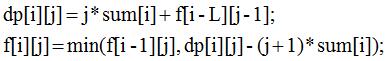
代码:
#include<cstdio> #include<cstring> #include<cmath> #include<queue> #include<vector> #include<iostream> #include<algorithm> #include<bitset> #include<functional> using namespace std; const int maxn = 20000 + 10; const int INF = 0x7fffffff; int dp[maxn][100 + 10]; int f[maxn][100 + 10]; int a[maxn]; int sum[maxn]; int n, l, k; int ans; void read() { scanf("%d%d%d", &n, &k, &l); for (int i = 1; i <= n; i++) scanf("%d", &a[i]); } void init() { memset(sum, 0, sizeof sum); for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + a[i]; ans = INF; for (int i = 0; i <= n; i++) for (int j = 0; j <= k; j++) dp[i][j] = INF, f[i][j] = INF; } void work() { for (int i = l; i <= n; i++) { dp[i][1] = sum[i]; f[i][1] = min(f[i - 1][1], dp[i][1] - (1 + 1)*sum[i]); } for (int i = 1; i <= n; i++) { for (int j = 2; j <= k; j++) { if (i - l <= 0) continue; if (f[i - l][j - 1] == INF) continue; dp[i][j] = j*sum[i] + f[i - l][j - 1]; f[i][j] = min(f[i - 1][j], dp[i][j] - (j + 1)*sum[i]); } } for (int j = 1; j <= k; j++) ans = min(ans, dp[n][j]); //for (int j = 1; j <= k; j++) printf("**** %d\n", dp[n][j]); printf("%d\n", ans); } int main() { int T; scanf("%d", &T); while (T--) { read(); init(); work(); } return 0; }


