将军令
题目链接:https://www.luogu.org/problemnew/show/P3942
题解:
当k一定且很小(1或2)时,明显这就成了一道树形dp。也就是说如果你写过HNOI2003消防局的设立的话这道题就可以至少拿75分。(或者你花上几个小时推出+调试k=3时的dp方程就可以拿到90分啦qaq)
但是这道题显然不是这么做的。其实我们只要稍稍贪心一下即可。一个明显的性质是在能控制到一个节点的情况下,小队的深度越浅越好。(因为这样它就可以控制更多的点)。
我们先任选一个节点为根,把无根树转化成有根树。然后遍历整棵树,维护子节点对父亲节点的要求。再以子节点的信息更新父亲节点即可。
我们设v[x]表示节点x上方距离v[x]一定要有一个小队。(当v[x]==1时就是x节点的父亲节点一定要是小队)。那么比较容易发现的更新条件就是:叶子节点的v[]为k;当一个节点的子节点中有一个的v[]为1时该节点就一定是小队;一个小队节点的v[]为(2*k+1);不满足上述条件时v[x]=min{v[y]|y是x的子节点}-1。
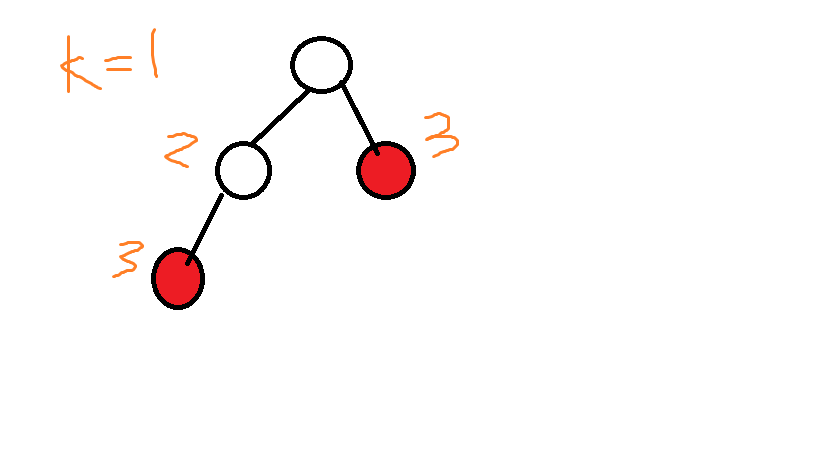
但是其实上述思路是有漏洞的。比如当k=1时,其左孩子的v[]为2,其右孩子的v[]为3时,其实该节点的v[]值为2。(因为他左子树中未被覆盖的点可以被右子树覆盖)。我放张图大家理解一下:
运用数学归纳法(其实就是找规律qwq)可以得出的结论是:对于节点x的子节点y来说,若v[y]+maxx>=2*k+3(maxx为x节点的子节点中最大的v[]值),则该子节点y不需被考虑。
另外,当k==0时该方法无法处理,所以我加了个特判。(当然你也可以在dfs时处理,但加个特判显然更方便=-=)。

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<vector> #define LL long long #define RI register int using namespace std; const int INF = 0x7ffffff ; const int N = 1e5 + 10 ; inline int read() { int k = 0 , f = 1 ; char c = getchar() ; for( ; !isdigit(c) ; c = getchar()) if(c == '-') f = -1 ; for( ; isdigit(c) ; c = getchar()) k = k*10 + c-'0' ; return k*f ; } struct Edge { int to, next ; }e[N<<1] ; int n, k, t, ans = 0 ; int head[N] ; inline void add_edge(int x,int y) { static int cnt = 0 ; e[++cnt].to = y, e[cnt].next = head[x], head[x] = cnt ; } int v[N] ; // x:上面距离x位置一定要有一个小队 void dfs(int x,int f) { int y ; vector<int>hh ; for(int i=head[x];i;i=e[i].next) { y = e[i].to ; if(y == f) continue ; dfs(y,x) ; } int mi = INF, mx = -INF ; for(int i=head[x];i;i=e[i].next) { y = e[i].to ; if(y == f) continue ; hh.push_back(v[y]) ; mx = max(mx,v[y]), mi = min(mi,v[y]) ; } if(mi == INF) { v[x] = k ; return ; } sort(hh.begin(),hh.end()) ; int mm = hh.size(), i ; for(i=0;i<mm;i++) { if(hh[i]+mx < (k<<1)+3) break ; } if(i == mm) { v[x] = mx-1 ; } else if(f == 0) { ans ++ ; } else if(hh[i] == 1) { ans ++ ; v[x] = (k<<1)+1 ; } else v[x] = hh[i]-1 ; } int main() { n = read(), k = read(), t = read() ; if(!k) { printf("%d",n) ; return 0 ; } int x, y ; for(int i=1;i<n;i++) { x = read(), y = read() ; add_edge(x,y) ; add_edge(y,x) ; } dfs(1,0) ; printf("%d",ans) ; return 0 ; }
——end ;


