树的重量

  题目链接：https://www.luogu.org/problemnew/show/P1268

 

  题解：

　　首先我们考虑当n=2时的情况，则ans=e[1][2]。

　　当n等于3时，则可以看3是从1,2之间的链上分叉出来的。（题目保证了对于任意i、j、k，e[i][j] <= e[i][k]+e[k][j]）

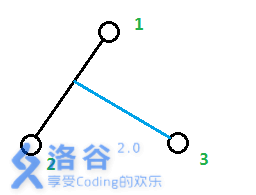
　　则新增长度为蓝色部分。此时新增长度len=（e[1][3]+e[2][3]-e[1][2]）/2 。

　　当n=4时，假如是下面这种情况：

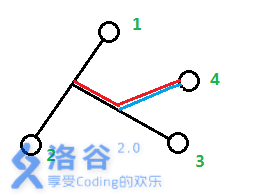
　　则如果我们把4看做是从1与2之间的链上分叉出来的，则新增长度为红色部分，而如果我们把4看做从1与3 或 2与3之间的链上分叉出来的，则新增长度为蓝色部分，很明显我们想要的是蓝色部分。所以我们要枚举已经被插入树上的节点，看看在哪两个之间插入会使得新增长度最小。

　　而我们可以发现其实每个节点插入的时候都可以看做是从某一对节点之间的链上分叉出来的，而且对后面插入的节点无影响。所以我们只要寻找当前最优即可。

　　并且对于一棵已知的最优的树，我们可以观察到以任意的顺序插入都可以最终构成该树。所以我们直接按节点编号枚举即可。

 

（图片来自luogu题解中的TsReaper大佬，在此对其表示感谢）

 

#include<iostream>
#include<cstdio>
#include<cstring>
#define LL long long
#define RI register int
using namespace std;
const int INF = 0x7ffffff ;
const int N = 30 + 2 ;

inline int read() {
    int k = 0 , f = 1 ; char c = getchar() ;
    for( ; !isdigit(c) ; c = getchar())
      if(c == '-') f = -1 ;
    for( ; isdigit(c) ; c = getchar())
      k = k*10 + c-'0' ;
    return k*f ;
}
int hh[N][N] ;

int main() {
    int n ;
    while(1) {
        n = read() ;
        if(!n) return 0 ;
        int x ;
        for(int i=1;i<=n;i++) {
            for(int j=i+1;j<=n;j++) {
                hh[i][j] = read() ;
            }
        }
        int ans = hh[1][2] ;
        for(int i=3;i<=n;i++) {
            int len = INF ;
            for(int j=1;j<i-1;j++) {
                for(int k=j+1;k<i;k++) {
                    x = (hh[j][i]+hh[k][i]-hh[j][k])>>1 ;
                    if(x < 0) continue ;
                    len = min(len,x) ;
                }
            }
            ans += len ;
        }
        printf("%d\n",ans) ;
    } 
    return 0 ;
}