test0704
test 0704
T1 餐馆
得分情况
期望：100
实际：100
题意
共有 \(n\) 种食材,一份食材 \(i\) 需要花 \(t_i\) 小时不间断地进行播种,施肥,直至收获。当然,一份食材 \(i\) 是可以直接卖掉得到 \(w_i\) 块钱的。
招牌菜共有 \(m\) 种,一份招牌菜 \(i\) 需要消耗一定的食材,花 \(T_i\) 小时不间断地来烹饪,叫卖,并最终卖出得到 \(W_i\) 块钱。
整个季度换算下来一共有 \(T_{max}\) 小时可供你使用
正解
这？菜和食材是一个东西……
然后直接完全背包……
T2 烯烃
得分情况
期望：100
实际：80
改后：100
题意
给你一棵树,一些边有标记,对于每条有标记的边,在树中找到包含这条边的一条最长链,并输出长度。
犯傻原因
其实是数据的问题
询问有 \(0\) ???
询问的点比 \(n\) 大？？？
离谱……
然后改了些细节解决了这个越界问题……
正解
直接按照求直径的DP预处理 \(down_x\) 和 \(up_x\) 的值，表示下面最长的距离和上面最长的距离，答案就是 \(down_x+up_x\)
T3 三米诺
得分情况
期望：40
实际：40
改后：
题意
用三米诺覆盖 \(3 \times n\) 的矩形棋盘,共多少种方案?
三米诺可旋转;两种方案不同当且仅当这两种图案直接覆盖在一起无法重叠。
犯傻原因
式子都出来了但是我竟然没想到直接错位相减然后就可以了矩阵快速搞了……
正解
不想放图片，直接开讲。
首先设 \(f[n]\) 为长度为 \(n\) 的时候答案是多少。
然后我们考虑怎么递推到 \(f[n]\)
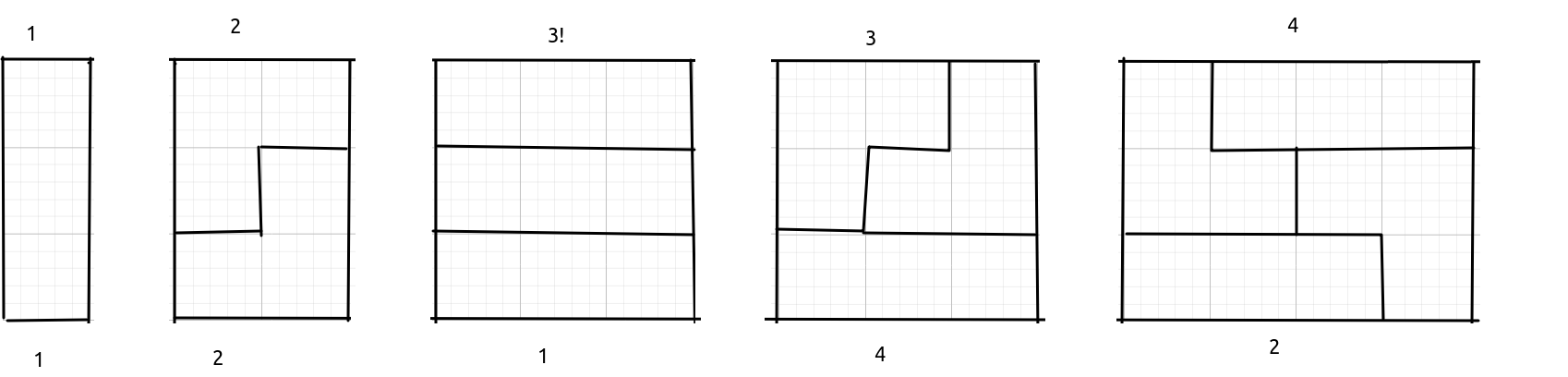
对于上图来说上面是长度，下面是情况数，这些都是两边为竖直的直线，中间没有切开的（有切开就会算重复）。
然后我们就可以来搞一手了，
至于为什么是有 \(\sum\)
我们可以想一下，在每一行中间的位置插入一个 \(1 \times 3\) 的方块，是不是还是满足上面加粗限制？？？
所以就有了这么一个式子，然后显然你可以前缀和然后就有40分了……
然后我们想想怎么优化，不用前缀和，这样我们就可以使用矩阵快速冥……
显然错位相减……
然后就懒得写了
再然后……
直接矩乘
考试总结
这次……
没啥好说的没出什么问题……
不过对于式子还是要多推下看看能不能优化然后拿到更高的分数。
