实验三 计算机九班周天意202383290419

一、实验目的

1. 能正确使用c语法规则定义、声明、调用函数
2. 能正确编写递归函数
3. 针对具体问题场景，能合理抽象出独立的功能模块，正确定义函数并使用，使得代码更具可读性、
可维护性
4. 针对具体问题场景，能正确、合理使用全局变量和局部static变量，解决实际问题
二、实验准备

实验前，请复习第4章以下内容：
1. 函数定义、声明、调用的语法规则
2. 什么是形参、什么是实参，以及，参数传递和返回过程
3. 什么是递归函数，以及，递归函数的编写规范
4. 全局变量、局部static变量的特性
三、实验内容

1. 实验任务1
在c开发环境下，输入如下程序。结合注释和运行结果，理解程序的功能，观察源代码中是如何使用函数
模块组织代码的。

2. 实验任务2
在c开发环境下，输入如下程序:
task2_1.c

#include <stdio.h>
long long fac(int n); // 函数声明

int main() {
    int i, n;

    printf("Enter n: ");
    scanf("%d", &n);

    for (i = 1; i <= n; ++i)
        printf("%d! = %lld\n", i, fac(i));

    return 0;
}

// 函数定义
long long fac(int n) {
    static long long p = 1;

    p = p * n;

    return p;
}

3. 实验任务3
已知数学函数式如下：（限定n取值范围为[0, 32]）
设计一个函数模块func()，用来实现：提供n的数值，返回该函数计算式的结果。
要求：
使用递归算法实现
不使用标准库函数pow()
提示*: 根据数学关系式，找出f(n)和f(n-1)的关系，把n阶问题转换为n-1阶问题。
补足代码task3.c中的函数模块定义部分，实现题目要求。
4. 实验任务4
编写函数计算组合数，要求算法分别用迭代方式和递归方式实现。
设函数原型如下： int func(int n, int m); 其功能是计算从n个不同元素中取出m个元素的组合数。
main函数代码已经在task4.c中给出，补足函数func()的定义，实现题目要求。
补足代码task4.c中函数模块定义部分，分别用两种方式实现函数：
实现方式1：迭代方式
实现方式2：递归方式
5. 实验任务5
对教材「例4.9 Hanoi塔问题」稍做改写，使其满足以下要求：
支持多组输入：输入不同的n值，打印输出不同的移动盘子方案
对于每个n，除了打印盘子移动方案之外，还要打印输出移动盘子的总次数

6. 实验任务6
编写函数func，实现将一个长整型数s的每一数位上的奇数依次取出来，构成一个新的数，高位仍在高
位，低位仍在低位，返回这个新数。例如，s=20231030时，调用函数fun后，返回313。
在主函数中，通过多组输入方式，多次调用fun()，实现对多组数据的测试。

四、实验结论

1、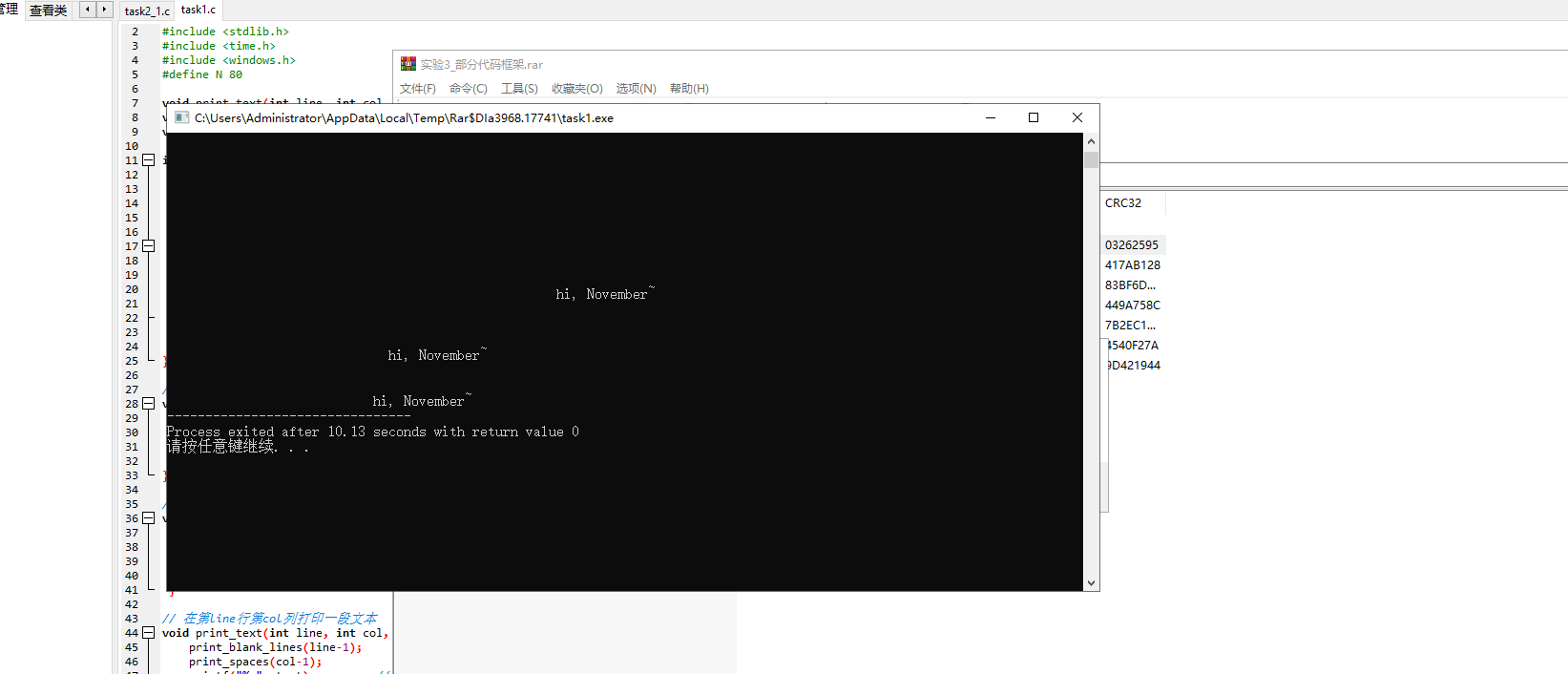

作用：以当前系统时间作为随机种子，在一秒为间隔各行各列打印10条语句

2、

#include <stdio.h>
long long fac(int n); // 函数声明

int main() {
    int i, n;

    printf("Enter n: ");
    scanf("%d", &n);

    for (i = 1; i <= n; ++i)
        printf("%d! = %lld\n", i, fac(i));

    return 0;
}

// 函数定义
long long fac(int n) {
    static long long p = 1;

    p = p * n;

    return p;
}

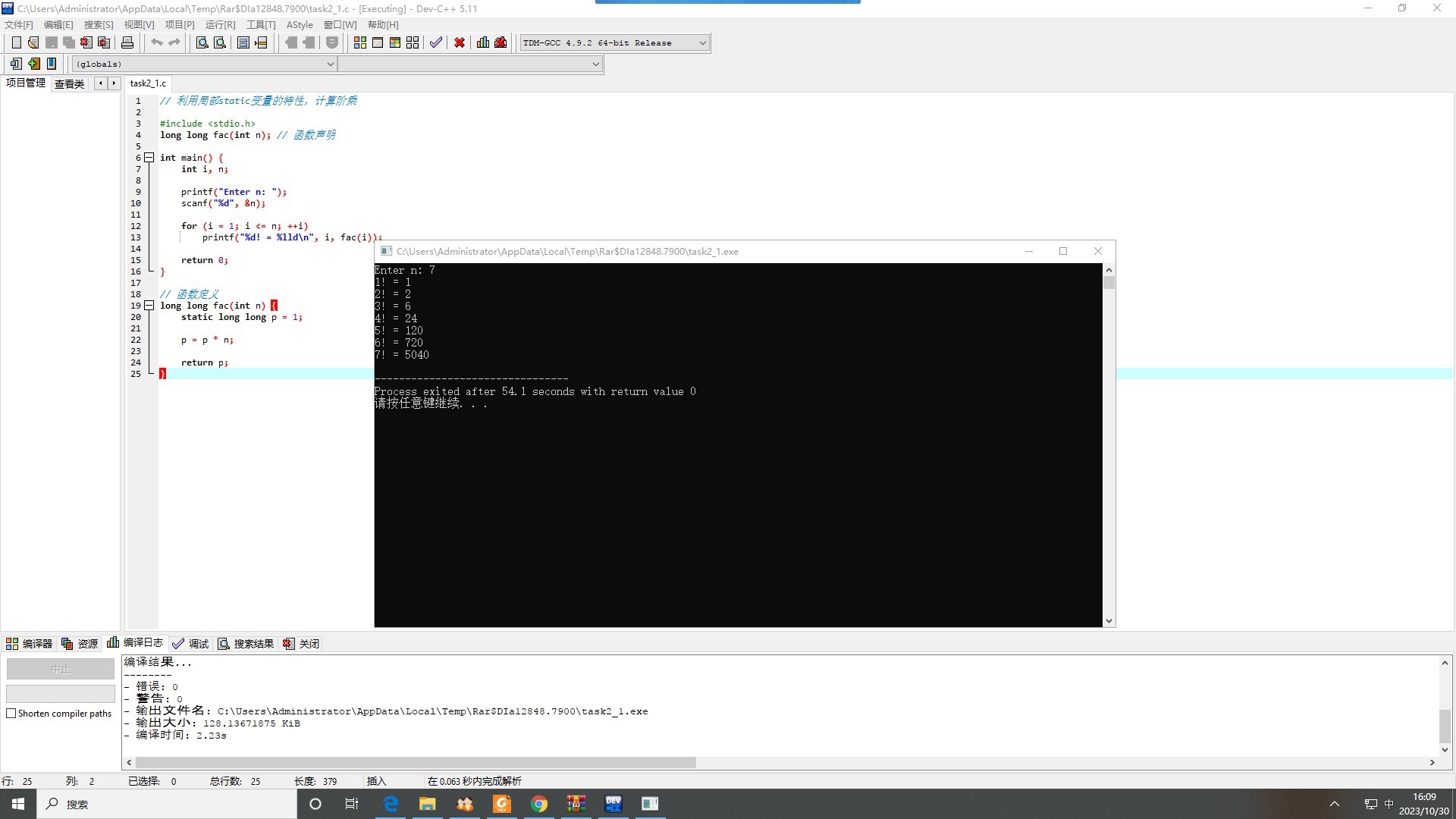
功能：使用静态变量的性质使变量的值被共享，且被永远改变，以此来实现阶乘

第二种情况

结果与预想一致

 

 

3、

#include<stdio.h>
int fun(int n);
int main(){
    int n,f;
//    printf("Entry n:");
//    scanf("%d",&n);
//    f = fun(n);
//    printf("n = %d f = %d",n,f);
//    return 0;
//} 
    while (scanf("%d", &n) != EOF) {
    f = fun(n); // 函数调用
    printf("n = %d, f = %lld\n", n, f);
    } 
    return 0;
    } 
int fun(int n){
    if(n ==1){
        return 1;
    }else{
        return 2 * fun(n - 1) + 1;
    }
}

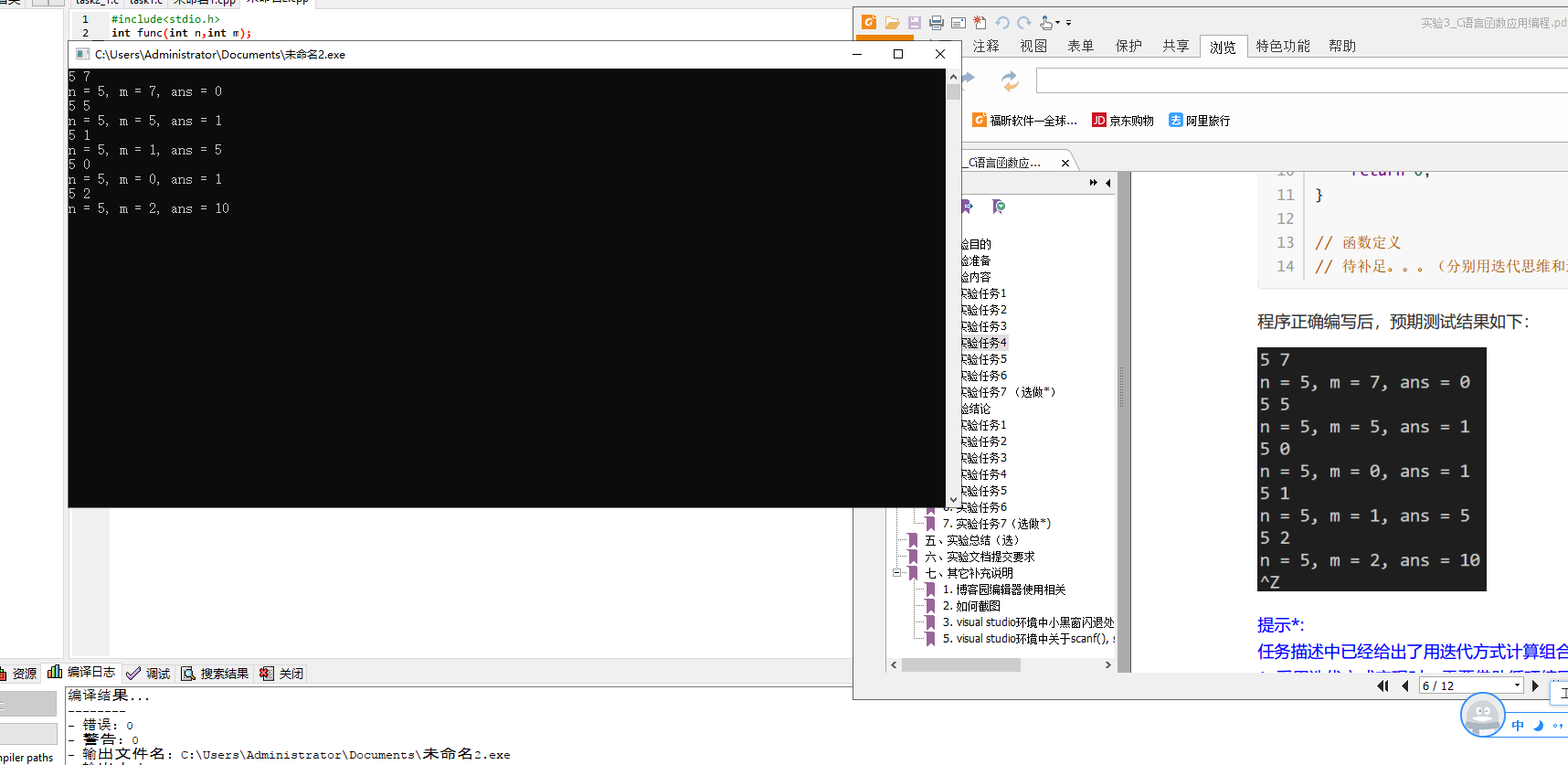
4、4. 实验任务4
此部分书写内容：
用迭代方式实现计算组合数 func() 的完整源代码task4_1.c，及，运行测试截图
用递归函数实现计算组合数 func() 的完整源代码task4_2.c，及，运行测试截图

#include<stdio.h>
int func(int n,int m);
int main(){
    int n,m;
    
    while(scanf("%d%d",&n,&m) != EOF){
        printf("n = %d, m = %d, ans = %d\n",n,m,func(n,m));
    }
    return 0;
}
//迭代方法 
int func(int n,int m){
    if(m > n){
        return 0;
    }else if(n == m || m == 0){
        return 1;
    }else{
        return func(n -1,m) + func(n -1,m -1);
    }
}

5、对教材「例4.9 Hanoi塔问题」稍做改写，使其满足以下要求：
支持多组输入：输入不同的n值，打印输出不同的移动盘子方案
对于每个n，除了打印盘子移动方案之外，还要打印输出移动盘子的总次数

#include<stdio.h>
void move(char A,char C,int n);
void Han(char A, char B, char C ,int n);
int count;
int main(){
    int n;
    
    while(scanf("%d",&n) != EOF){
        Han('A','B','C',n);
        printf("一个移动了%d次",count);
    }
    return 0;
} 
void move(char A,char C,int n){
    printf("%d : %c -- > %c",n,A,C);
    count++;
}
void Han(char A, char B, char C ,int n){
    if(n ==1){
        move(A,C,n);
    }else{
        Han(A,C,B,n -1);
        move(A,C,n);
        Han(B,A,C,n -1);
    }
     
}