CF580E Kefa and Watch 题解

花了一个半个下午+半个晚上终于调出来了......

0. 题面

长度为 \(n\) 的字符串，每个字符是 \(\mathtt{0} \sim \mathtt{9}\) 的数位，\(m + k\) 种操作：

1. 格式为 1 l r c，表示将 \(l \sim r\) 赋值为 \(c\)，保证 \(0 \le c \le 9\)。这种修改操作恰好 \(m\) 个。

2. 格式为 2 l r d，表示询问 \(l \sim r\) 是否有长度为 \(d\) 的循环节。这种询问操作恰好 \(k\) 个。

数据范围：\(n \leqslant 10^5\)，\(m + k \leqslant 10^5\)，\(0 \leqslant c \leqslant 10\)，\(1 \leqslant d \leqslant r - l + 1\)。

Translated by @attack

1. 思路

其实这道题的技术含量不太高，就是建一个维护区间哈希值的线段树而已，但是细节实在是太多了/kk

还有一个小结论：字符串 \(s\) 拥有长度为 \(d\) 的循环节 \(\Longleftrightarrow\) \(s[1,|s|-d]=s[d+1,|s|]\) 。感性证明如下图：

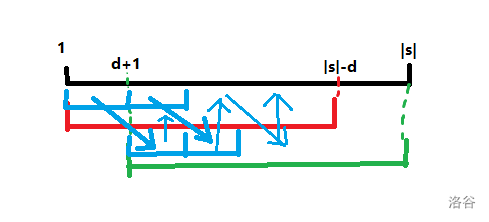
2. 坑

• 合并两个串的哈希值时应该让左侧的串乘以 \(base^{右侧的串长度}\) ，不要犯迷糊
• query() 中 \(R>mid\) 时可能存在 \(R>r\) ，要取个min
• CF 题比较喜欢卡自然溢出哈希，有些常见哈希模数也会被卡
• pushDown() 函数里不要忘记赋值 lazy 标记（这都是什么智障错误
• 要特判 \(L>R\) 的情况
• 不要忘记删调试语句

另外提一嘴，有时候把代码写得面向对象一点是有好处的，尤其是数据结构题。例如这题，如果把一个字符串的哈希值看成一个类就可以把合并操作封装起来，可以极大提升代码可读性，没准我就不用调这么久了......

3. 代码

丑陋的代码如下：

#include <iostream>
#include <string>
using namespace std;
const int MAXN=100000;
typedef unsigned long long ull;
const ull BASE=13,P=1000000009;
ull s[10][MAXN+5],base[MAXN+5];
struct SegmentTree{
    ull tr[MAXN*4+5];
    char lazy[MAXN*4+5];
    void pushUp(int p,int l,int r){
        int mid=(l+r)/2;
        tr[p]=(tr[p*2]*base[r-mid]+tr[p*2+1])%P;
    }
    void pushDown(int p,int l,int r){
        if(lazy[p]){
            int mid=(l+r)/2;
            tr[p*2]=s[lazy[p]-'0'][mid-l+1];
            tr[p*2+1]=s[lazy[p]-'0'][r-mid];
            lazy[p*2]=lazy[p*2+1]=lazy[p];
            lazy[p]=0;
        }
    }
    void modify(int p,int l,int r,int L,int R,char c){
        if(L<=l&&r<=R){
            tr[p]=s[c-'0'][r-l+1];
            lazy[p]=c;
        }else{
            pushDown(p,l,r);
            int mid=(l+r)/2;
            if(L<=mid){
                modify(p*2,l,mid,L,R,c);
            }
            if(R>mid){
                modify(p*2+1,mid+1,r,L,R,c);
            }
            pushUp(p,l,r);
        }
    }
    ull query(int p,int l,int r,int L,int R){
        if(L>R)return 0;
        if(L<=l&&r<=R){
            return tr[p];
        }else{
            pushDown(p,l,r);
            int mid=(l+r)/2;
            ull res=0;
            if(L<=mid){
                res=query(p*2,l,mid,L,R);
            }
            if(R>mid){
                res=(res*base[min(R,r)-mid]%P+query(p*2+1,mid+1,r,L,R))%P;
            }
            return res;
        }
    }
}tr;
int n,m,k;
char str[MAXN+5];
int main(){
    ios::sync_with_stdio(false);
    cin>>n>>m>>k>>str+1;
    for(int i=0;i<=9;i++){
        s[i][0]=0;
        for(int j=1;j<=n;j++){
            s[i][j]=(s[i][j-1]*BASE%P+i+'0')%P;
        }
    }
    base[0]=1;
    for(int i=1;i<=n;i++){
        base[i]=base[i-1]*BASE%P;
    }
    for(int i=1;i<=n;i++){
        tr.modify(1,1,n,i,i,str[i]);
    }
    for(int t=1;t<=m+k;t++){
        int op,l,r,u;cin>>op>>l>>r>>u;
        if(op==1){
            tr.modify(1,1,n,l,r,u+'0');
        }else{
            if(tr.query(1,1,n,l,r-u)==tr.query(1,1,n,l+u,r)){
                cout<<"YES"<<endl;
            }else{
                cout<<"NO"<<endl;
            }
        }
    }
    return 0;
}