斜率优化动态规划 学习笔记

首先看这样一个问题：

洛谷 P3195 [HNOI2008]玩具装箱
题目大意:
有 \(n\) 个物品排成一行,第 \(i\) 个物品权值为 \(C_i\) ,现要求将这些物品分成若干段,每段的花费为 \(((\sum_{i=l}^{r}{C_i})-L)^2\) (其中 \(l\),\(r\) 为这一段的左右端点, \(L\) 为给定常数),问最小的总花费.保证 \(1 \leq n \leq 5 \times 10^4\)，\(1 \leq L \leq 10^7\)，\(1 \leq C_i \leq 10^7\) .

这题显然是一道 DP 题. 令 \(dp_{i}\) 为考虑前 \(i\) 个物品的最小代价, \(sum_i=\sum_{j=1}^{i}C_j\) , 可以想出这样的状态转移方程:

\[dp_i=\min_{0\le j<i}\{dp_j+(sum_i-sum_{j}-L)^2\} \]

然而, 如果暴力转移时间复杂度是 \(\Theta(n^2)\) 的, 显然会T, 有什么办法优化吗?

动态规划优化的一个重要思路是把可能决策的范围缩小 (即排除不可能的决策) . 顺着这个思路试试看?

首先我们观察状态转移方程, 发现这个 \(\min\) 函数很碍事, 把它去掉:

\[dp_i=dp_j+(sum_i-sum_{j}-L)^2 \]

这个方程太长了, 所以考虑令 \(a_i=sum_i-L\) , \(b_i=sum_i\) , 代入得:

\[dp_i=dp_j+(a_i-b_j)^2 \]

这个平方也很碍事, 把它展开:

\[dp_i=dp_j+{a_i}^2-2a_ib_j+{b_j}^2 \]

把跟 \(i\) 有关的移到等号一边, 跟 \(j\) (读作"勾") 有关的放到另一边:

\[2a_ib_j+dp_i-{a_i}^2=dp_j+{b_j}^2 \]

......感觉直到现在我们做的都是一些很常规的操作...... 但是如果我们放一个直线的表达式跟它对比一下?

\((2a_i)b_j+(dp_i-{a_i}^2)=(dp_j+{b_j}^2)\)

\(kx+b=y\)

于是我们惊奇地发现, 状态转移方程竟然可以看作一条斜率为 \(2a_i\) , 截距为 \(dp_i-{a_i}^2\) 的直线和一个在 \((b_j,dp_j+{b_j}^2)\) 的点(我管它叫决策点)!

所以, "转移" 这个过程就可以理解为找到一个斜率为 \(2a_i\) 的直线交于一个已有的决策点.

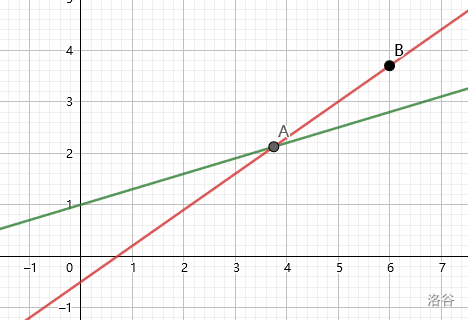
其中, 红色直线表示 \(dp_i\) 对应的直线,绿色直线表示一个可能的 \(dp_j\) 对应的直线, 点 A 表示这个 \(dp_j\) 对应的决策点, 点 B 表示 \(dp_i\) 对应的决策点.

所以我们怎么找一条最优的直线, 使得 \(dp_i\) 最小? 难道要枚举 \(j\) 吗?

当然不用. 因为 \(dp_i-{a_i}^2\) 只与 \(i\) 有关, 所以只要这条直线的截距最小, \(dp_i\) 就是最小的. 我们假设平面上已经有一堆可供转移的决策点和直线:

可以想象 \(dp_i\) 对应的直线从下往上移动 (别忘了这条直线的斜率不变) , 显然它第一个接触到的点就是最优决策点.

如果您学过计算几何 (我没学过QAQ) , 您可以马上发现潜在的最优决策点都在这一堆点的下凸包上!

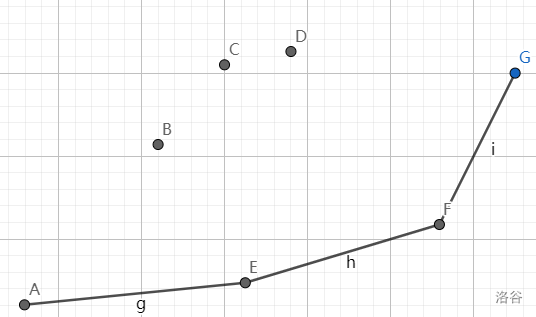
所以我们只需要用一个单调队列来维护这个凸包就可以了.

具体怎么维护等到以后再写罢, 博主累了.

综上所述, 我们通过发掘状态转移方程的性质做到了摊还 \(\Theta(1)\) 的转移, 非常优秀.

代码:

#include <iostream>
#include <queue>
using namespace std;
typedef long long ll;
#define int ll
const int MAXN=50000;
int n,L,c[MAXN+5],sum[MAXN+5],dp[MAXN+5];
deque<int> q;
int a(int i){return sum[i]+i;}
int b(int i){return sum[i]+i+L+1;}
int X(int i){return b(i);}
int Y(int i){return (dp[i])+(b(i)*b(i));}
double slope(int i,int j){return double(Y(i)-Y(j))/double(X(i)-X(j));}
signed main(){
    ios::sync_with_stdio(false);
    cin>>n>>L;
    for(int i=1;i<=n;i++){
        cin>>c[i];sum[i]=sum[i-1]+c[i];
    }
    q.push_back(0);
    for(int i=1;i<=n;i++){
        double qwq=114514.1919810;
        if(q.size()>=2)qwq=slope(q[0],q[1]);
        while(q.size()>=2&&slope(q[0],q[1])<double(2*a(i))){
            q.pop_front();
        }
        int j=q.front();
        dp[i]=dp[j]+(a(i)-b(j))*(a(i)-b(j));
        while(q.size()>=2&&slope(q[q.size()-1],q[q.size()-2])>slope(q[q.size()-2],i))q.pop_back();
        q.push_back(i);
    }
    cout<<dp[n]<<endl;
    return 0;
}