学习笔记 网络流

1.引入

想象这样一个场景：自来水厂和您家分别坐落在城市的两端。自来水厂可以以任意速率生产水，您家可以以任意速率接受水。您家和自来水厂之间有一些中转站和水管，水管有最大流速限制（即每单位时间最多流多少单位水），中转站不能存水，只能输进多少就马上吐出多少。

这个东西就是网络流。把这个问题数学化就便乘了这样：

假设 \(G(V,E)\) 是一个有限的有向图，它的每条边 \((u,v) \in E\) 都有一个非负值实数的容量 \(c(u,v)\) 。如果 \((u,v)\) 不属于 \(E\) ，我们假设 \(c(u,v) = 0\) 。我们区别两个顶点：一个源点 \(s\) 和一个汇点 \(t\)。一道网络流是一个对于所有结点 \(u\) 和 \(v\) 都有以下特性的实数函数 \(f(u,v)\)

容量限制 (Capacity Constraints): \(f(u,v)≤c(u,v)\) 一条边的流不能超过它的容量。

斜对称 (Skew Symmetry): \(f(u,v)=-f(v,u)\) 由 \(u\) 到 \(v\) 的净流必须是由 \(v\) 到 \(u\) 的净流的相反（参考例子）。（既然要看网络流，这是一定要知道的）

流守恒 (Flow Conservation):除非 \(u=s\) 或 \(u=t\) ，否则 \(\sum_{w\in V}f(u,w)=0\) ——结点的净流是零，除了“制造”流的源点和“消耗”流的汇点。

注意 \(f(u,v)\) 是由 \(u\) 到 \(v\) 的净流。如果该图代表一个实质的网络，由 \(u\) 到\(v\) 有 \(4\) 单位的实际流及由 \(v\) 到 \(u\) 有 \(3\) 单位的实际流，那么\(f(u,v) = 1\) 及 \(f(v,u) = − 1\) 。

以上内容摘自百度百科 链接：[https://baike.baidu.com/item/网络流/2987528]

2.最大流

您观察了这个宏伟的管道系统，想问一个问题：您家最多能以多大的速率用水？（即：找到一个流函数 \(f\)，使得 \(\sum_{w\in V} f(w,t)\) 最大）这就是最大流问题。

2.1.Ford-Fulkerson 算法

一个简单的想法是每次从源点到汇点找一条路径，再把这条路径上的每条边的剩余容量减去这条路径上的“瓶颈”（即最小流量），每条边的反向边的剩余容量加上“瓶颈”（方便反悔）。（这种路径被称为增广路，找增广路之后的图被称为残量网络）这就是 Ford-Fulkerson 算法。

然而，可以构造这样一个图，使得它跑得贼慢：

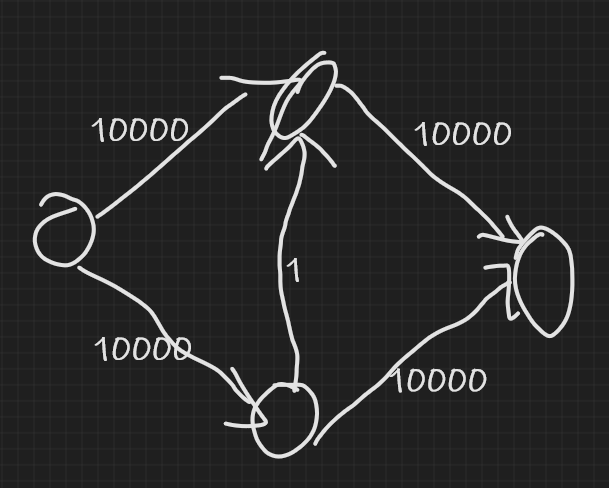
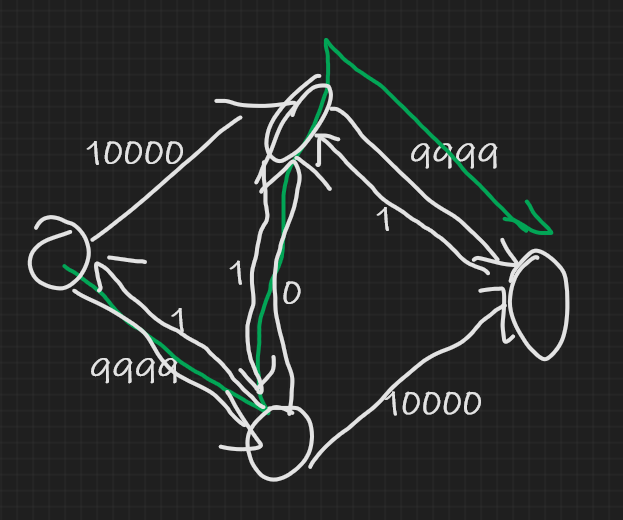
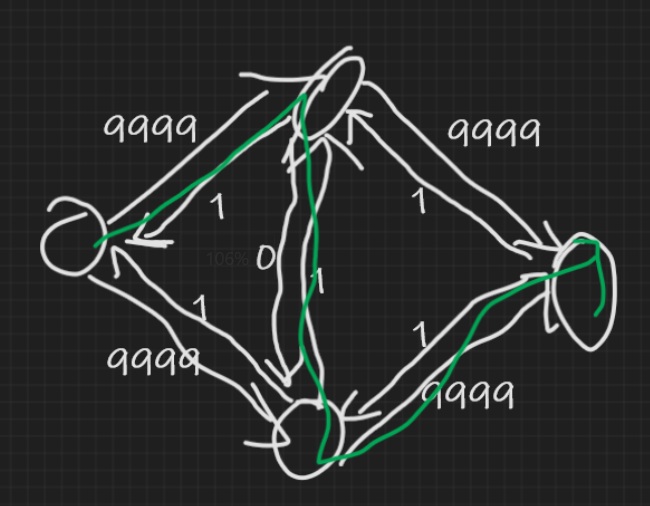
容易发现，中间的那条边会被反复增广再反悔。有没有什么办法避免这种情况？

2.2.Edmond-Karp 算法

一个想法是每次通过 BFS 找到源点到汇点的最短路进行增广，这就是 Edmond-Karp 算法的思想。它的时间复杂度为 \(O(nm^2)\)，但一般跑不满。

代码如下：

bool bfs(){//BFS找增广路
    memset(pre,0,sizeof(pre));
    memset(dis,0,sizeof(dis));
    memset(vis,0,sizeof(vis));
    queue<int> q;
    q.push(s);
    dis[s]=INF;vis[s]=true;
    while(q.size()){
        int u=q.front();
        q.pop();
        if(u==t)return true;
        for(int i=g.head[u];i!=0;i=g.g[i].next){
            int v=g.g[i].v,&w=g.g[i].w;
            if(w&&!vis[v]){
                dis[v]=min(dis[u],w);
                pre[v]=i;//记录增广路
                q.push(v);
                vis[v]=true;
            }
        }
    }
    return false;
}
int Edmonds_Karp(){
    int res=0;
    while(bfs()){
        int now=t;
        while(now!=s){
            g.g[pre[now]].w-=dis[t];
            g.g[pre[now]^1].w+=dis[t];//一个小技巧，把边和反向边在数组中成对存储，^1之后的编号就是反向边的编号。
            now=g.g[pre[now]^1].v;
        }
        res+=dis[t];
    }
    return res;
}

2.3.Dinic 算法

Edmond-Karp 算法虽然效率较高，但能不能再优化一下呢？当然能！

还有一个想法是先按照到源点的距离在图上“分层”，再用 DFS 找增广路，找增广路时强制只能从上一层走到下一层。这就是 Dinic 算法。具体细节请参照代码：

int level[MAXN+5];//记录每一个点的层次
bool bfs(){//分层
    memset(level,0,sizeof(level));
    queue<int> q;
    q.push(s);
    level[s]=1;
    while(q.size()){
        int u=q.front();
        q.pop();
        for(int i=g.head[u];i;i=g.g[i].next){
            int v=g.g[i].v,w=g.g[i].w;
            if(w>0&&level[v]==0){
                level[v]=level[u]+1;
                q.push(v);
            }
        }
    }
    if(level[t])return true;
    else return false;
}
int dfs(int u,int dis){//找增广路
    if(u==t){
        return dis;
    }else{
        int out=0;
        for(int i=g.head[u];i;i=g.g[i].next){
            int v=g.g[i].v,&w=g.g[i].w;
            if(w>0&&level[v]==level[u]+1){
                int nxt=dfs(v,min(w,dis));
                if(nxt){
                    w-=nxt;
                    g.g[i^1].w+=nxt;
                    dis-=nxt;
                    out+=nxt;
                }
            }
        }
        if(out==0)level[u]=-1;//如果当前点被榨干了就撇了它
        return out;
    }
}
int Dinic(){
    int res=0;
    while(bfs()){
        while(int tmp=dfs(s,INF)){
            res+=tmp;
        }
    }
    return res;
}

3.费用流

现在自来水公司要对每条水管收费了。每条水管都有一个价格，每流一滴水都要收若干块钱。现在您想问，如果您家以最大的速率用水，您一个单位时间最少要花多少钱？

一个简单的想法是每次按价格跑一遍 SPFA，再沿最短路增广，重复增广知道找不到增广路为止。

代码：

int dis[MAXN+5],flow[MAXN+5];
int pre[MAXN+5];
bool SPFA(){
    memset(dis,0x3f,sizeof(dis));
    memset(flow,0,sizeof(flow));
    dis[s]=0;
    flow[s]=0x3f3f3f3f;
    queue<int> q;
    q.push(s);
    while(q.size()){
        int u=q.front();
        q.pop();
        for(int i=head[u];i;i=g[i].nxt){
            int v=g[i].v,w=g[i].w,c=g[i].c;
            if(w&&dis[u]+c<dis[v]){
                dis[v]=dis[u]+c;
                flow[v]=min(flow[u],w);
                pre[v]=i;
                q.push(v);
            }
        }
    }
    return dis[t]!=0x3f3f3f3f;
}
pair<int,int> SSP(){
    int max_flow=0,cost=0;
    while(SPFA()){
        int u=t;
        while(u!=s){
            int t1=pre[u];
            g[t1].w-=flow[t];
            g[t1^1].w+=flow[t];
            u=g[t1^1].v;
        }
        max_flow+=flow[t];
        cost+=flow[t]*dis[t];
    }
    return make_pair(max_flow,cost);
}

4.结尾

网络流的题目主要考察的其实不是网络流算法本身，而是如何建模。建议做一做网络流24题来练习。