主席树/函数式线段树/可持久化线段树 初步 学习笔记

主席树/函数式线段树/可持久化线段树 初步 学习笔记

1.什么是主席树？

主席树是一种由许多棵 重叠的 值域线段树构成的数据结构，可以维护很多跟值域有关的信息。

2.怎么写主席树？

先来看一道例题（区间第 \(k\) 小）：

洛谷P3834 【模板】可持久化线段树 2

题目大意:给定 \(n\) 个整数构成的序列 \(a\)，将对于指定的闭区间 \([l,r]\) 查询其区间内的第 \(k\) 小值。

先离散化一下。考虑用值域线段树来维护这个东西，一个非常暴力的思路就是建 \(n\) 棵线段树，第 \(i\) 棵线段树维护区间 \([1,i]\) 的信息，对于区间 \([l,r]\) 只需把第 \(r\) 棵线段树和第 \(l-1\) 棵线段树做差再查第 \(k\) 小。这样做的时间复杂度是 \(O(n^2)\) 的，时间也是 \(O(n^2)\) 的 （时空两开花） ，显然会炸。

有没有优化的方法？当然有！

注意到一件事：

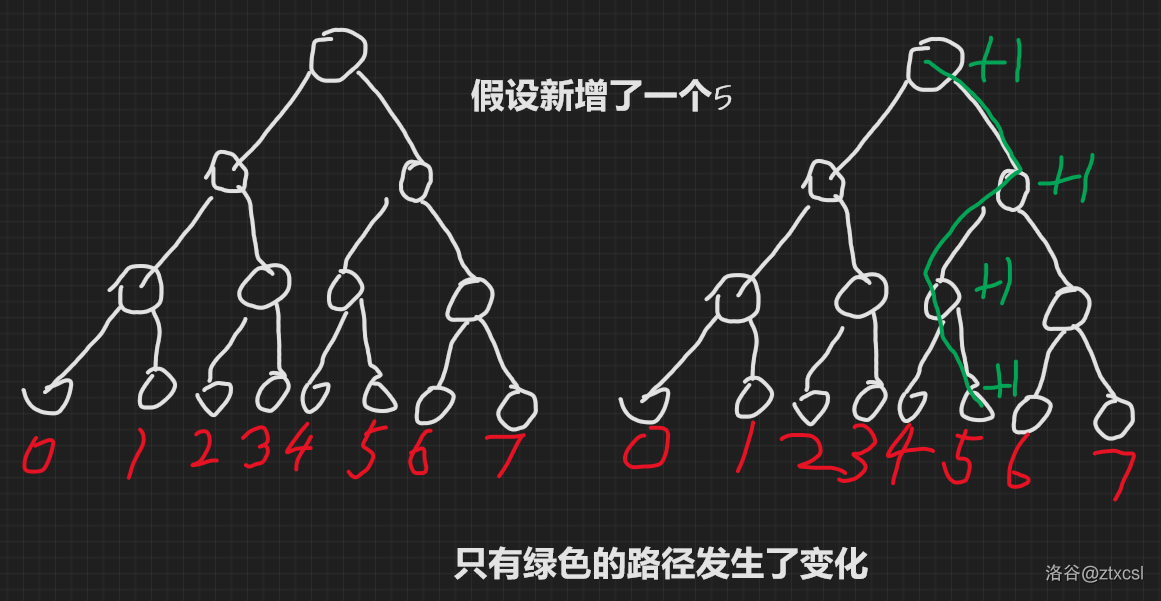
如果把其他的节点复制一遍显然太浪费了，所以可以在新建一棵线段树时复用这些节点。像这样：

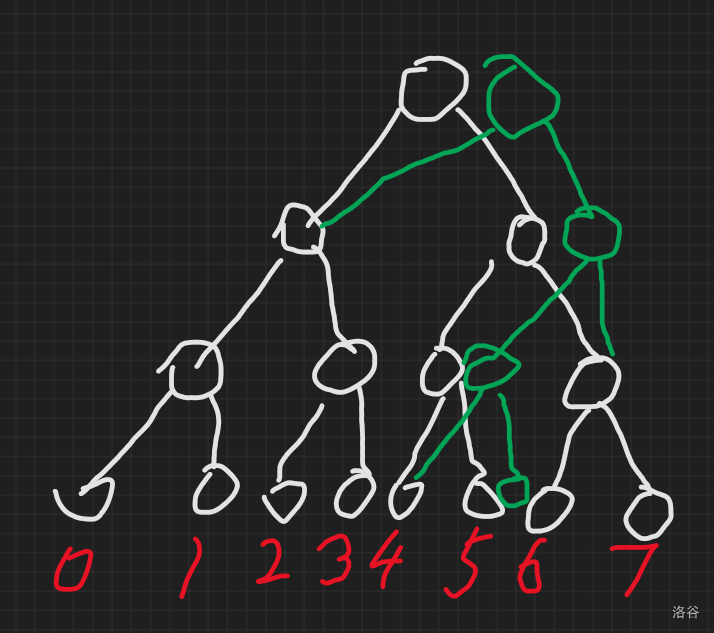
如果我们把绿色树根作为根节点，对这颗新线段树进行访问，它的效果跟完全新建一棵线段树是一样的，却只使用 \(O(\log{n})\) 的时间和空间，非常的高效。这就是 可持久化 的思想。

代码：

#include <iostream>
#include <map>
#include <algorithm>
using namespace std;
const int MAXN=200000;
struct segment_tree{
    int sum;
    int lp,rp;
    segment_tree *ls,*rs;
    segment_tree(){sum=0;lp=rp=0;ls=rs=NULL;}
    void build(int l,int r){//新建一棵空白树
        lp=l;rp=r;
        if(l<r){
            int mid=(l+r)/2;
            ls=new segment_tree;
            ls->build(l,mid);
            rs=new segment_tree;
            rs->build(mid+1,r);
        }
    }
    void push_up(){
        sum=ls->sum+rs->sum;
    }
    segment_tree* add(int x,int k){//可持久化地修改
        segment_tree* res=new segment_tree(*this);
        if(lp==rp){
            res->sum+=k;
        }else{
            if(x<=ls->rp){
                res->ls=ls->add(x,k);
            }
            if(x>=rs->lp){
                res->rs=rs->add(x,k);
            }
            res->push_up();
        }
        return res;
    }
};
int kth(segment_tree*l,segment_tree*r,int k){//求第k大
    if(l->lp==l->rp){
        return l->lp;
    }else{
        int lcnt=r->ls->sum-l->ls->sum;//做差
        if(k<=lcnt){
            return kth(l->ls,r->ls,k);
        }else{
            return kth(l->rs,r->rs,k-lcnt);
        }
    }
}
int n,m,a[MAXN+5];
segment_tree *trees[MAXN+5];
map<int,int> mp1;
int mp2[MAXN+5];
void lsh(){//离散化
    for(int i=1;i<=n;i++){
        mp2[i]=a[i];
    }
    sort(mp2+1,mp2+1+n);
    for(int i=1;i<=n;i++){
        mp1[mp2[i]]=i;
    }
    for(int i=1;i<=n;i++){
        a[i]=mp1[a[i]];
    }
}
int main(){
    ios::sync_with_stdio(false);
    cin>>n>>m;
    trees[0]=new segment_tree;
    trees[0]->build(1,n);
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    lsh();
    for(int i=1;i<=n;i++){//建主席树
        trees[i]=trees[i-1]->add(a[i],1);
    }
    for(int i=1;i<=m;i++){
        int l,r,k;cin>>l>>r>>k;
        cout<<mp2[kth(trees[l-1],trees[r],k)]<<endl;
    }
    return 0;
}

3.主席树的效率如何？

主席树通过这道例题的时空复杂度均为 \(O(n\log{n})\)，非常高效。