KMP算法详解

-1.前置约定

如非特殊说明，以下文字中$T$代表主串，$P$代表模式串，$m$代表主串长度，$n$代表模式串长度

真前缀 一个字符串除了它本身之外的前缀。例如，moo 是 moon 的真前缀，moon 却不是。真后缀同理。

“border” 如果字符串 $a$ 既是 $b$ 的真前缀，又是 $b$ 的真后缀，那么我们说 $a$ 是 $b$ 的 border。

0.什么是KMP？

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度$O(m+n)$。——摘自百度百科

简而言之，它可以在 $O(m+n)$ 的时间复杂度之内在主串 $T$ 中找到所有模式串 $P$，非常优秀。

1.正文

1.1.求$next$数组

KMP算法需要求一个“$next$数组”，$next_i$= $P_{1...i}$ 最大的border的长度

注意到border有一些很好的性质，例如：

1. 传递性。如果 $a$ 是 $b$ 的 border， $b$ 是 $c$ 的 border，那么 $a$ 是 $c$ 的 border。
2. 如果 $a$ 是 $s$ 的 border,那么比 $a$ 小的最大 $s$ 的 border 一定是 $a$ 的最大 border。 换句话说，把 $s$ 的所有 border 从大到小排序，那么在后面的 border 也是在前面的 border 的 border。

根据上面两个性质可以推出这样一个有趣的结论：如果知道 $next_{1...i-1}$ ，就可以找出字符串的所有 border ！

所以 $next_i$ 、 $next_{next_i}$ 、 $next_{next_{next_i}}$ ......是所有字符串 $P_{1..i}$ 的 border 的长度。老套娃了

于是我们可以根据这个性质递推出 $next$ 数组。

根据 $next$ 数组的定义，显然有 $next_1=0$。

假设 $next_1$ 到 $next_{i-1}$都已经被求出来了。如果当前要求 $next_i$ ，我们只需让 $j$ 依次等于 $next_{i-1}$ 、 $next_{next_{i-1}}$ 、 $next_{next_{next_{i-1}}}$...... （$P_{1...i-1}$ 所有 border 的长度），因为 border 的定义， $P_{1...j}==P_{i-j...i-1}$ 总是成立，所以如果 $P_{j+1}==P_{i}$ ，就说明 $P_{1...j+1}==P_{i-j...i}$ ，即找到了 $P_{1..i}$ 的一个 border。

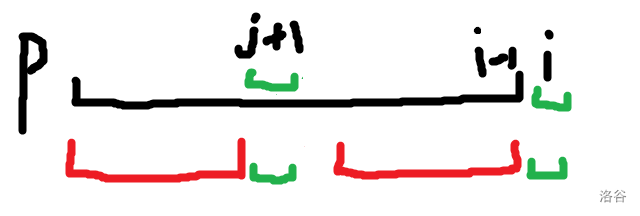
不难看出，最先找到的 border 一定是最大的 border ,即 $next_i$。

于是可以写出求 $next$ 数组的代码：

next[1]=0;
for(int i=2;i<=n;i++){
    int j=next[i-1];
    while(j>0&&p[i]!=p[j+1]){
        j=next[j];
    }//让j依次等于P[1...i-1]的所有border
    if(p[i]==p[j+1]){
        j++;
    }
    next[i]=j;
}

1.2.匹配

先来看看暴力算法的思路。

然而我们可以发现，它的时间复杂度甚至达到了$O(mn)$。在暴力算法中，如果发生了失配（即匹配到半路发现有一个字符不相等），只能把模板串往后移1位再重新开始匹配。这样做效率实在太低了，有什么办法优化吗？

当然有！

如果发生下列情况：

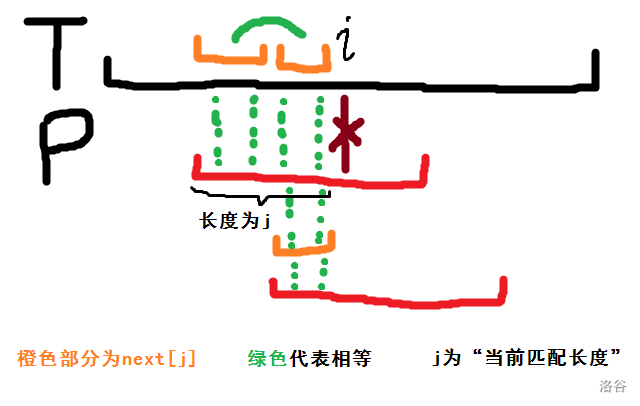
可以直接把模板串后移 $j-next_j$ 位，即令 $j$ 赋值为 $next_j$。如果仍然失配，就重复以上过程，直到匹配成功为止，然后进行下一轮匹配。

这个东西跟求 $next$ 数组思想类似，代码肯定也类似啦233

代码：

for(int i=1,j=0;i<=m;i++){
    while(j>0&&t[i]!=p[j+1]){
        j=next[j];
    }
    if(t[i]==p[j+1]){
        j++;
    }
    if(j==n){//匹配成功！OHHHHHHHHHHHHHH！
        cout<<i-j+1<<endl;//输出位置
        j=next[j];//不能躺在功劳簿上睡大觉，重新开始下一轮匹配！
    }
}

1.3 时间复杂度

匹配过程的时间复杂度乍一看很高，因为它有两重循环。实际上，内层循环的执行次数一定不超过 $m$ 次，因为每一次内层循环至少会让 $j$ 减少 $1$，每一次外层循环至多会让 $j$ 加上 $1$，所以内层循环执行次数一定不超过外层循环，即 $m$ 次。所以，不难看出整个匹配过程的时间复杂度为 $\Theta(m)$ 。

求 $next$ 数组过程好像不能通过以上方法分析，然而它还有一种等价写法，也是我常用的写法：

next[1]=0;
for(int i=2,j=0;i<=n;i++){
    while(j>0&&p[i]!=p[j+1]){
        j=next[j];
    }//让j依次等于P[1...i-1]的所有border
    if(p[i]==p[j+1]){
        j++;
    }
    next[i]=j;
}

这样，也不难看出求 $next$ 数组过程的时间复杂度为 $\Theta(n)$

综上，整个 KMP 算法的时间复杂度为 $\Theta(m+n)$，非常快。

2.总结

KMP 算法的精髓在于废旧信息的重新利用和发掘问题性质，同时这也是一个非常烧脑的算法， 非常巧妙。

再附赠一份能通过模板题的代码：

#include <iostream>
#include <cstring>
using namespace std;
#define MAXN 1000000
int nxt[MAXN + 5], n, m;
char t[MAXN + 5], p[MAXN + 5];
int main() {
    ios::sync_with_stdio(false);
    cin >> t + 1 >> p + 1;
    m = strlen(t + 1);
    n = strlen(p + 1);
    nxt[1] = 0;
    for (int i = 2; i <= n; i++) {
        int j = nxt[i - 1];
        while (j > 0 && p[i] != p[j + 1]) {
            j = nxt[j];
        }
        if (p[i] == p[j + 1]) {
            j++;
        }
        nxt[i] = j;
    }
    for (int i = 1, j = 0; i <= m; i++) {
        while (j > 0 && t[i] != p[j + 1]) {
            j = nxt[j];
        }
        if (t[i] == p[j + 1]) {
            j++;
        }
        if (j == n) {
            cout << i - j + 1 << endl;
            j = nxt[j];
        }
    }
    for (int i = 1; i <= n; i++) {
        cout << nxt[i] << ' ';
    }
    return 0;
}

所以，都看到这里了，能给我点一个赞吗（逃