《大话数据结构》 -- 程杰

第一章数据结构绪论

数据结构：是相互之间存在一种或多种特定关系的数据元素的集合

1.5 逻辑结构与物理结构/存储结构

1.5.1 逻辑结构

逻辑结构：是指数据对象中数据元素之间的相互关系

1.集合结构
集合结构：集合结构中的数据元素除了同属于一个集合外，他们之间没有其他关系

2.线性结构
线性结构：线性结构中的数据元素之间是一对一的关系

3.树形结构
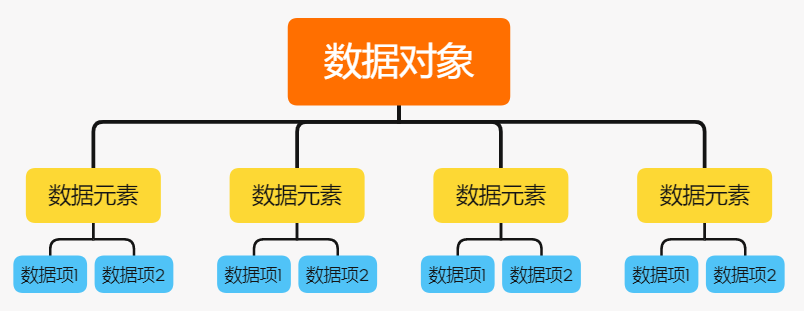
树形结构：树形结构中的数据元素之间存在一种一对多的层次关系

4.图形结构
图形结构：图形结构的数据元素是多对多的关系

1.5.2 物理结构

物理结构：是指数据的逻辑结构在计算机中的存储形式

1.顺序存储结构
顺序存储结构：是把数据元素存放在地址连续的存储单元里，其数据间的逻辑关系和物理关系是一致的

2.链式存储结构
链式存储结构：是把数据元素存放在任意的存储单元里，这组存储单元可以是连续的，也可以是不连续的。
数据的存储关系并不能反映其逻辑关系，因此需要用一个指针存放数据元素的地址，这样通过地址就可以找到相关联数据元素的位置

抽象是指抽取出事物具有的普遍性的本质

1.6.2 抽象数据类型

抽象数据类型（ADT）：一个数学模型及定义在该模型上的一组操作
抽象数据类型的定义仅取决于它的一组逻辑特性，而与其在计算机内部如何表示和实现无关

抽象数据类型体现了程序设计中问题分解、抽象和信息隐藏的特性

抽象数据类型的标准格式：

ADT 抽象数据类型名
Data
  数据元素之间逻辑关系的定义
Operation
操作1
    初始条件
    操作结果描述
操作2
    ...
操作n
    ...
endADT

第一章总结

逻辑结构有：

集合结构
线性结构
树形结构
图形结构

物理结构有：

顺序存储结构
链式存储结构

第二章算法

算法是解决特定问题求解步骤的描述，在计算机中表现为指令的有限序列，并且每条指令表示一个或多个操作

2.5 算法的特性

算法具有五个基本特性：输入、输出、有穷性、确定性和可行性

输入输出：算法具有0个或多个输入，至少有一个或多个输出
有穷性：算法在执行有限的步骤之后，自动结束而不会出现无限循环，并且每一个步骤在可接受的时间内完成
确定性：算法的每一步骤都具有确定的含义，不会出现二义性
可行性：算法的每一步都能通过执行有限次数完成

2.6 算法设计的要求

正确性：指算法至少应该具有输入、输出和加工处理无歧义性，能正确反映问题的需求，能够得到问题的正确答案
可读性：算法设计的另一目的是为了便于阅读、理解和交流
健壮性：当输入数据不合法时，算法也能做出相关处理，而不是产生异常或莫名其妙的结果
时间效率高和存储量低

2.7 算法的度量方法

一个程序的运行时间，依赖于算法的好坏和问题的输入规模（输入量的多少）

2.8 函数的渐进增长

最终在分析程序的运行时间时，最重要的是把程序看成是独立于程序设计语言的算法或一系列步骤

判断一个算法的效率时，函数中的常数和其他次要项常常可以忽略，而更应该关注主项（最高阶项）的阶数

2.9 算法时间复杂度

2.9.1 算法时间复杂度定义

分析算法复杂度，关键就是要分析循环结构的运行情况

用大写O()来体现算法事件复杂度的记法，也叫大O记法

常数阶：单纯的分支结构（不包含在循环结构中），其时间复杂度也是O(1)

线性阶：O(n)

对数阶：O(logn)

平方阶：循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数

2.10 常见的时间复杂度

平均运行时间时所有情况中最有意义的，因为它是期望的运行时间

一般在没有特殊说明的情况下，都是指最坏时间复杂度

2.1.2 算法空间复杂度

算法的空间复杂度通过计算算法所需的存储空间实现
算法空间复杂度的计算公式记作：S(n) = O(f(n)) n为问题的规模，f(n)为语句关于n所占存储空间的函数

若输入数据所占空间只取决于问题本身，和算法无关，这样只需要分析该算法在实现时所需的辅助单元即可。
若算法执行时所需的辅助空间相对于输入数据量而言是个常数，则称此算法为原地工作，空间复杂度为O(1)

第二章总结

算法的定义、特性、设计的要求、度量方法、函数的渐进增长
算法时间复杂度的定义和推导大O阶的步骤

推导大O阶很容易，但如何得到运行次数的表达式确是需要数学功底的

第三章线性表：0个或多个数据元素的有限序列

3.2 线性表的定义

线性表是一个序列，元素之间有顺序，是有限的

在较复杂的线性表中，一个数据元素可以由若干个数据项组成

3.3 线性表的抽象数据类型

线性表的抽象数据类型定义如下：

ADT 线性表(list)
Data
    线性表的数据对象集合为{a1,a2,...,an}，每个元素的类型均为DataType。其中除第一个元素a1外，每一个元素有且只有一个直接前驱元素，除了最后一个元素an外，每一个元素有且只有一个直接后继元素。数据元素之间的关系是一对一的关系

Operation
    InitList(*L):初始化操作，建立一个空的线性表L
    ListEmpty(L):若线性表为空，返回true，否则返回false
    ClearList(*L):将线性表清空
    GetElem(L,i,*e):将线性表L中的第i个位置元素值返回给e
    LocationElem(L,e):在线性表L中查找与给定值e相等的元素，如果查找成功，返回该元素在表中序号表示成功；否则，返回0表示失败
    ListInsert(*L,i,e):在线性表L中的第i个位置插入新元素e
    ListDelete(*L,i,*e):删除线性表L中第i个位置元素，并用e返回其值
    ListLength(L):返回线性表L的元素个数
endADT

/*将所有的在线性表Lb中但不在La中的数据元素插入到La中*/
void unionL(SqList *La,SqList Lb)
{
    int La_len,Lb_len,i;
    ElemType e;					//声明与La和Lb相同的数据元素e
    La_len=ListLength(*La);		//求线性表的长度
    Lb_len=ListLength(Lb);
    for (i=1;i<=Lb_len;i++)
    {
        GetElem(Lb,i,&e);		//取Lb中第i个数据元素赋给e
        if (!LocateElem(*La,e))	//La中不存在和e相同数据元素
            ListInsert(La,++La_len,e);	//插入
    }
}

当你传递一个参数给函数的时候，这个参数会不会在函数内被改动决定了使用什么参数形式

如果需要被改动，则需要传递指向这个参数的指针

如果不用被改动，可以直接传递这个参数

posted @ 2021-07-04 16:14 ztw1002 阅读(946) 评论(0) 编辑收藏举报

刷新页面返回顶部

ztw1002