201871030140-朱婷婷 实验三 结对项目—《D{0-1}KP 实例数据集算法实验平台》项目报告

项目 内容
课程班级博客链接 2018级卓越班
这个作业要求链接 实验三 结对项目
我的课程学习目标 1.体验软件项目开发中的两人合作，练习结对编程；
2.掌握GitHub协作开发程序的操作方法。
这个作业在哪些方面帮助我实现学习目标 1.知道了结对编程的重要性；
2.理解了代码风格和设计规范、结对编程；
3.了解了代码复审的各种形式及其目的；
4进一步熟悉并掌握了PSP；
5.掌握了GitHub协作开发程序的操作方法。
结对方学号-姓名 201871030118-雷云云
结对方本次博客作业链接 结对方的博客
本项目GitHub的仓库链接地址 Experiment-3

任务1：阅读《现代软件工程—构建之法》第3-4章内容

  • 代码规范

    代码规范可以分成两个部分：

    • 代码风格规范：

      主要是文字上的规定。代码风格的原则是简明、易读、无二义性，本着“保持简明，让代码更容易读”的原则。

      1.缩进：4个空格的距离。不用Tab键的理由是，Tab键在不同的情况下会显示不同的长度，严重干扰阅读体验。

      2.括号：在复杂的条件表达式中，用括号清楚地表示逻辑优先级。

      3.分行：不要把多条语句放在一行上， 更严格地说，不要把多个变量定义在一行上。

      4.下划线：用来分隔变量名字中的作用域标注和变量的语义。

      5.大小写：所有的类型/类/函数名都用Pascal形式，所有的变量都用Camel形式。

    • 代码设计规范：

      牵涉到程序设计、模块之间的关系、设计模式等方方面面的通用原则。

  • 代码复审

    代码复审就是看代码是否在“代码规范”的框架内正确地解决了问题。软件工程中最基本的复审手段，就是同伴复审。

    名称 形式 目的
    自我复审 自己 vs. 自己 用同伴复审的标准来要求自己。不一定有效，因为开发者对自己总是过于自信。如果持之以恒，则对个人有很大好处。
    同伴复审 复审者 vs. 开发者 简便易行
    团队复审 团队 vs. 开发者 有比较严格的规定和流程、适用于关键的代码，以及复审后不再更新的代码；覆盖率高——有很多双眼睛盯着程序，但效率可能不高。

    • 代码复审前：

      1.代码必须成功地编译，在所有要求的平台上，同时要编译Debug|Retail版本。

      2.程序员必须测试过代码。

    • 代码复审后：

      1.更正明显的错误。

      2.对于无法很快更正的错误，要在项目管理软件中创建Bug把它们记录下来。

      3.把所有的错误记在自己的一个“我常犯的错误”表中，作为以后自我复审的第一步。

  • 结对编程

    结对编程让两个人所写的代码不断地处于“复审”的过程，程序员们能够不断地审核，提高设计和编码质量，可以及时发现并解决问题，避免把问题拖到后面的阶段去。开发中的复审主要包括：设计复审、代码复审、测试计划复审和文档复审。这些复审可以在伙伴之间进行，也可以在团队内部进行。

    • 什么是结对编程：

      结对编程（Pair programming）是一种敏捷软件开发的方法，两个程序员在一个计算机上共同工作。一个人输入代码，而另一个人审查他输入的每一行代码。输入代码的人称作驾驶员，审查代码的人称作观察员（或导航员）。两个程序员经常互换角色，结对编程是极端编程的组成部分。

    • 结对编程的好处：

      1.在开发层次，结对编程能提供更好的设计质量和代码质量，两人合作解决问题的能力更强。

      2.对开发人员自身来说，结对工作能带来更多的信心，高质量的产出能带来更高的满足感。

      3.在企业管理层次上，结对能更有效地交流，相互学习和传递经验，分享知识，能更好地应对人员流动。

      总之，如果运用得当，结对编程可以取得更高的投入产出比。

任务2：对结对方的项目成果进行评价

  • 对项目博文作业进行阅读并进行评论

    认真阅读了结对方的项目博文作业，并从博文结构、博文内容、博文结构与PSP中“任务内容”列的关系、PSP中“计划共完成需要的时间”与“实际完成需要的时间”两列数据的差异化分析与原因四个方面进行了评论。

    评论链接：评论

  • 克隆结对方项目源码并测试运行

    阅读结对方的代码并测试运行。输入背包容量、物品个数以及重量和价值后，可以选择解决0-1背包问题的算法，运行的结果如下图所示。选择动态规划算法后程序运行错误，没有输出最后的结果。


  • 复审同伴项目代码

    • 概要部分：

      代码基本符合需求，设计考虑的不够周全，同伴的代码中包括动态规划算法和回溯算法求解0-1背包问题的过程，用户可以选择其中的一种算法进行求解，但是要求的部分功能还未实现。代码的可读性比较好，且易于维护。

    • 设计规范部分：设计遵从项目中常用的模式，存在一小部分无用的代码可以清除。

    • 代码规范部分：修改的部分符合代码标准和风格。

    • 具体代码部分：对于调用的外部函数检查了返回值，参数传递无错误。

    • 可读性：代码可读性较好，而且有必要的注释，易于理解。

  • 对同伴个人项目仓库的源码进行合作修改

    • 结对方Github项目仓库链接：结对方的GitHub仓库

    • 使用仓库中的fork将结对方的仓库链接到自己的GitHub中

任务3：采用两人结对编程方式，设计开发一款D{0-1}KP 实例数据集算法实验平台

  • 需求分析陈述

    通常用户处理数据时的数据量比较大，而且不同的用户可能会使用不同的方法求解问题的解，所以，为了方便用户使用不同的方法求出0-1背包问题的最优解，提高处理大量数据的效率，我们需要设计开发一款D{0-1}KP 实例数据集算法实验平台。

    D{0-1}KP 实例数据集算法实验平台具有的功能如下：

    1. 平台基础功能：实验二 任务3；
    2. D{0-1}KP 实例数据集需存储在数据库；
    3. 平台可动态嵌入任何一个有效的D{0-1}KP 实例求解算法，并保存算法实验日志数据；
    4. 人机交互界面要求为GUI界面（WEB页面、APP页面都可）；
    5. 查阅资料，设计遗传算法求解D{0-1}KP，并利用此算法测试要求（3）；
    6. 附加功能：除（1）-（5）外的任意有效平台功能实现。

  • 软件设计说明

    在个人项目中绘制了一组数据的散点图，实现了对价值与重量之比进行排序，完成了用动态规划算法求解0-1背包问题，并计算出了运行的时间，此次结对项目是在个人项目的基础上进行了进一步的完善。

    • 增加使用回溯算法求解0-1背包问题

      back_tracking函数:

      进行回溯，在搜索的过程中可进行剪枝操作。当不选择此物品时，若此时所能达到的最大价值小于当前的最优价值，则进行剪枝操作，即不在继续向下搜索这个结点的子树。如果选择此物品，则判断背包的剩余重量是否大于当前物品的重量，如果小于当前物品的重量，则不装入。

      此函数最后返回记录物品是否装入的数组与最优价值。

      上界函数bound：

      判断当前物品下所能达到的最大价值。

    • 对动态规划算法进行修改

      在个人项目中，动态规划算法求解的最大价值是正确的，但是选择的物品出现了错误，进行修改之后能求得正确的结果。

    • 可以选择不同的方法求解问题

      从键盘输入一个字符，若它的值为”1“，则使用动态规划法求解，若为”2“就用回溯法求解，否则输出一条错误提示语句。

    • 将求解的结果保存在txt文件中

    • 学习并尝试使用遗传算法求解0-1背包问题

      GA是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式，利用计算机仿真运算，将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时，相对一些常规的优化算法，通常能够较快地获得较好的优化结果。遗传算法已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。

  • 软件实现及核心功能代码展示

    • 选择不同的算法：

      #选择不同的算法求解0-1背包问题
print("\n\n请选择解决0-1背包问题的算法：\n1.动态规划算法\n2.回溯算法\n")
print("请输入选项：", end=" ")
parm = input()
if parm == '1':
    #用动态规划算法求解
elif parm == '2':
    #用回溯法求解
else:
    print("出错啦！没有这个选项！")

    • 动态规划算法：

      class onezerobag:
    def __init__(self, w, v, c):
        self.w = w
        self.v = v
        self.c = c

    def dynamic_programming(self):
        self.v = np.array(self.v)
        self.w = np.array(self.w)
        num = self.v.size
        values = np.zeros([num+1, self.c+1])
        for i in range(values.shape[0]):
            values[i, 0] = 0
        for i in range(values.shape[1]):
            values[0, i] = 0
        for i in range(1, values.shape[0], 1):
            for j in range(1, values.shape[1], 1):
                if(self.w[i - 1] > j):
                    values[i,j] = values[i-1, j]
                else:
                    if(values[i-1,j]>values[i-1,j-self.w[i-1]]+self.v[i-1]):
                        values[i,j] = values[i-1, j]
                    else:
                        values[i,j]=values[i-1, j-self.w[i - 1]] + self.v[i - 1]
        return values

    def load_which(self, values):
        h = values.shape[0]
        c = self.c
        which = []
        for i in range(h-1, 0, -1):
            if(values[i,c] == values[i-1,c]):
                continue
            else:
                which.append(i)
                c = c - self.w[i - 1]
        which.reverse()
        return which, values[values.shape[0]-1, values.shape[1]-1]

    • 回溯算法：

      back_tracking函数:

      def back_tracking(self, i, visit):
    if(i > self.v.size-1):
        self.bestp = self.cp
        return

    if(self.cw + self.w[i] < self.c):
        self.cw += self.w[i]
        self.cp += self.v[i]
        visit[i] = 1
        self.back_tracking(i+1, visit)
        self.cw -= self.w[i]
        self.cp -= self.v[i]
    else:
        visit[i] = 0

    if(self.bound(i+1) >= self.bestp):
        self.back_tracking(i+1, visit)
    return visit, self.bestp

      上界函数bound：

      def bound(self, i):
    leftw = self.c - self.cw
    bestbound = self.cp
    while (i < self.v.size):
        if (self.w[i] <= leftw):
            bestbound = bestbound + self.v[i]
            leftw = leftw - self.w[i]
            i += 1
        else:
            bestbound = bestbound + self.v[i] / self.w[i] * leftw
            break
    return bestbound

    • 保存结果：

      data = open("结果.txt", "w")  # 创建保存结果文件
data.write('***回溯算法***\n背包中所装物品为：')  # 写入文件
for a in sorted(list):
    print(a, end=" ")
    s = str(a) + " "
    data.write(s)
print("\n最大价值为：", best)
print("运行时间为：%.3f秒"%(end1-start1))
data.write('\n最大价值为：')  # 写入文件
data.write(str(best))
data.write('\n运行时间为：')  # 写入文件
data.write(str(end1 - start1))
data.write('秒')

  • 程序运行

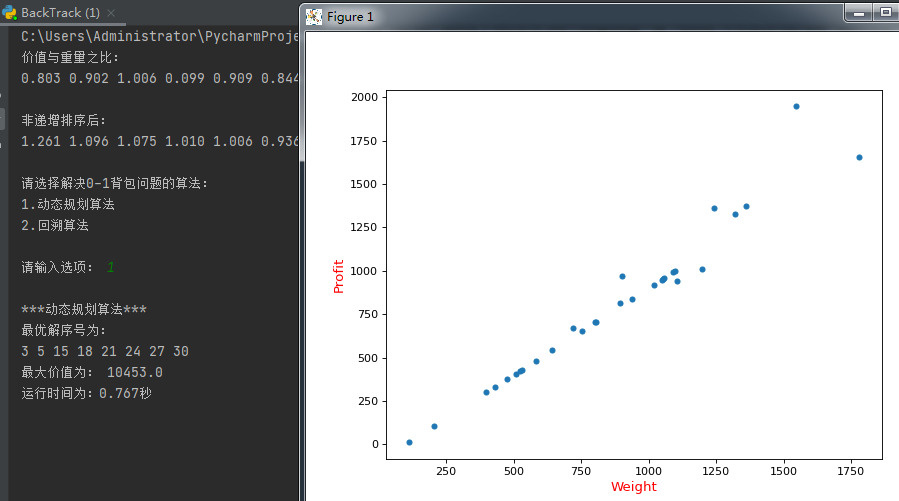
    • 动态规划算法：


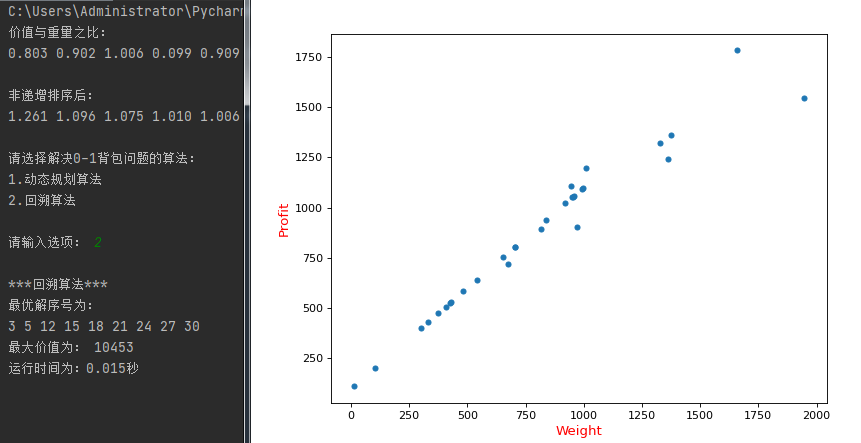
    • 回溯算法：


    • 保存结果：



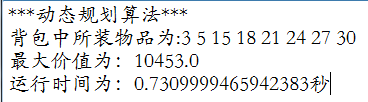
  • 结对的过程




  • 结对作业的PSP

任务内容 计划共完成需要的时间（h） 实际完成需要的时间（h）
计划 0.5 0.5
• 估计这个任务需要多少时间 0.5 0.5
开发 64.5 74
• 需求分析 1 1.5
• 生成设计文档 2 2
• 设计复审 3 3.5
• 代码规范 1 2
• 具体设计 2.5 3
• 具体编码 35 40
• 代码复审 8 7
• 测试 12 15
报告 1.9 2.6
• 测试报告 0.3 0.5
• 计算工作量 0.6 0.6
• 事后总结及过程改进计划 1 1.5

  • 小结感受

    1.通过阅读《构建之法》了解了代码风格规范和代码设计规范，知道了结对编程的概念，以及代码复审的种形式和目的。
    2.结合结对方对我的PSP评价，根据自身能力进行时间的估计和项目开发的计划，进一步熟悉并掌握了PSP，但是还需要继续学习，不断进步。
    3.对GitHub协作开发程序的操作方法不够熟练，在后续的学习中要不断实践并掌握。
    4.项目实现了其中的一部分功能，了解了遗传算法，但是没有完成用遗传算法求解0-1背包问题；GUI界面和数据库部分没有很好的完成，还要进一步完善。
    5.在此次结对项目中，我知道了结对编程的作用以及它的重要性，在编写代码的过程中遇到问题时，可以通过两个人讨论交流来共同解决，这样做不仅提高了效率，而且还能从结对方身上学到很多有用的东西。

posted on 2021-04-14 08:32  Rairy  阅读(88)  评论(1)  编辑  收藏  举报

Powered by: 博客园 Copyright © 2024 Rairy
Powered by .NET 9.0 on Kubernetes