字符串学习笔记

字符串学习笔记

哈希

最基础的字符串算法, 规定一个质数\(p\), 将字符串转换为一个\(p\)进制的数

字符串最小循环表示法

咕咕咕

KMP

定义需要被匹配的串叫做

我们知道暴力算法是在每一个位置开始匹配, 匹配不成功时位置++

这样的算法最好时间复杂度是\(O(原串长度)\), 最坏时间复杂度是\(O(原串长度*匹配串长度)\)

考虑对暴力算法的优化

我们知道对于一个字符串, 若它在当前位置匹配不成功, 并且出现了这样一个情况

这个红色和蓝色是满足相等的条件下的, 最长的前缀和后缀, 若此时指针在蓝色右边, 我们可以直接将指针移至红色端点右边, 继续匹配

对于一个字符串\(S\), 它的长度为\(n\)

我们设\(nxt[i]\)为满足对于\(S\)的一个字串\(S[1 - i]\), 有\(S[1 - nxt[i]]\) = \(S[(i - nxt[i] + 1) - i]\)这一条件的最大的下标

那么我们对于字符串匹配就有了这样的算法

	for(int i = 1; i <= n; i++)
	{
		while(pos && s2[pos + 1] != s1[i])
			pos = nxt[pos];//无法匹配时跳到nxt处继续匹配
		if(s2[pos + 1] == s1[i]) pos++;//若相等指针后移
		if(pos == m)//整个字符串完成匹配
		{
			printf("%d\n", i - pos + 1);
			pos = nxt[pos]; //重新开始匹配
		}
	}

现在所求就变成了怎么求nxt数组

我们考虑这样一个过程

拿\(S[1 - (i - 1)]\)与\(S[1 - i]\)匹配, 当原串的指针超出原串范围时, 此时匹配串的指针即为\(nxt[i]\)

因为此时\(S[1 - nxt[i]]\)与\(S[(i - nxt[i] + 1) - i]\)相同

若此时\(S[1 - nxt[i]]\)不为最长子串, 那么在上一次跳\(nxt\)时是不会跳到当前位置的, 而会跳到最长子串所在的位置

感性理解一波

对于每次新加上一个字母, 我们没有必要去重新匹配, 可以直接在原来的基础上继续匹配, 具体原因感性理解一下吧, 在两个不匹配的字符串的后面加上不同的字母对匹配是没有影响的

于是有

	for(int i = 2; i <= m; i++)
	{
		while(pos && s2[pos + 1] != s2[i])
			pos = nxt[pos];
		if(s2[pos + 1] == s2[i]) pos++;
		nxt[i] = pos; 
	}

我在学习的时候发现了一个问题, 是这样的, 有没有可能在从\(i\)跳到\(nxt[i]\)的过程中, 跳过了一些可能对答案造成贡献的点, 也就是:

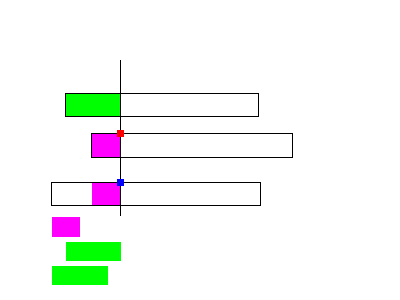
红点是\(i\), 蓝点是\(nxt[i]\), 紫串是\(S[1 - nxt[i]]\), 绿串是同时存在于前缀和后缀的一个比紫串更加长的子串

显然矛盾, 如果有这种情况, 那么\(nxt[i]\)就是绿色的左边了

康康别人的博客吧, 这个我自己能看懂就行

ExKMP

咕咕咕

后缀数组

咕咕咕

后缀自动机

咕咕咕

回文自动机

咕咕咕

AC自动机

咕咕咕

KMP自动机

咕咕咕

Manacher

咕咕咕