F - Largest Rectangle in a Histogram(单调栈)
题目地址:https://vjudge.net/contest/424167#problem/F
题目描述:
A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:
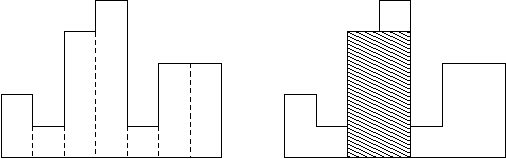
Usually, histograms are used to represent discrete distributions,
e.g., the frequencies of characters in texts. Note that the order of the
rectangles, i.e., their heights, is important. Calculate the area of
the largest rectangle in a histogram that is aligned at the common base
line, too. The figure on the right shows the largest aligned rectangle
for the depicted histogram.
题目大意:
给定一组宽度均为1的长方形的长度,求能够覆盖的最大长方形的面积。
7 2 1 4 5 1 3 3 4 1000 1000 1000 1000 0Sample Output
8 4000
一、题目简述
显然能够覆盖的最大面积是由某个长方形为出发点,向两边延展的结果。覆盖长方形的长必定是某个长方形的长,延展的尽头是当延展的长方形比选择的长方形要矮的时候。
二、暴力
2-1思路:
通过枚举每一个长方形,找到向左向右延伸的最远距离,计算得到的长方形面积并且对答案进行更新,这个思路十分简单。
2-2暴力代码:
while(1) { read(n); ans=0; if(0==n) break; for(int i=1;i<=n;i++) read(a[i]); for(int i=1;i<=n;i++) { int lim1=i,lim2=i; int limm=a[i]; for(int j=i+1;j<=n;j++) { if(limm>a[j]) break; else lim1=j; } for(int j=i-1;j>=1;j--) { if(limm>a[j]) break; else lim2=j; } ans=max(ans,(lim1-lim2+1)*a[i]); } printf("%lld\n",ans); }
时间复杂度是O(n2),对于这题105的上限来说显然是会TLE的。
2-3 利用dp思想优化暴力
总所周知,暴力出奇迹。以上的初步思想有了之后,我们可以想办法对其进行优化。
我们将某个长方形左边第一个比它矮的长方形称为它的左尽头,右边第一个比它矮的称为它的右尽头。
我们可以发现,对于选定的长方形A,如果A右边的某个长方形B比它高,那么直到长方形B的右尽头为止都会比A高,左边同理。
比如说:
1 2 3 4 5 0
0前面所有数字的右尽头是最后的那个0,当A为1,B为2的时候,我们可以通过B 知道3 4 5一定不是1的右尽头。
如此我们可以开两个数组l[N]和r[N],用来储存每一个长方形的左右尽头,这两个数组是可以进行传递的。
这种传递的DP思想我们可以得到表达式:
while(liml>1&&a[i]<=a[liml-1]) liml=l[liml-1];
右边同理:
2-4优化代码
while(1) { read(n); ans=0; if(0==n) break; for(int i=1;i<=n;i++) { read(a[i]); l[i]=i;r[i]=i; } for(int i=1;i<=n;i++) { int liml=i; while(liml>1&&a[i]<=a[liml-1]) liml=l[liml-1]; l[i]=liml; } for(int i=n;i>=1;i--) { int limr=i; while(limr<n&&a[i]<=a[limr+1]) limr=r[limr+1]; r[i]=limr; } for(int i=1;i<=n;i++) ans=max((r[i]-l[i]+1)*a[i],ans); printf("%lld\n",ans); } return 0;
这个思路是可以AC的。
三、单调栈
虽然暴力可以出奇迹,但是总是暴力心里空荡荡的。再一看这套题的标题。嗷!原来是数据结构。
对于延展这一过程进行模拟,我们发现延展过程中的单调递增性,如此我们想到这应当是一道单调栈或者单调队列的题目,通过模拟我们发现这是单调栈的题目。
实际上这就是一道单调栈的模板题。
3-1思路
我们从左到右维护一个高度单调递增的单调栈,当有高度进栈的时候,pop掉比当前高度高的栈顶高度,直到进栈后形成递增的趋势。
那么我们什么时候更新答案呢?当栈顶被pop的时候,更新栈顶为基准的延伸长方形的答案。
对于栈顶,使其pop的高度位置就是它的右尽头,它在栈内的前一个元素就是它的左尽头。
因此我们选择在站内维护每个长方形的位置信息。
举例来说:
2 1 4 5 1 3 3
2的位置1进栈,然后下一个是1,那么2将要pop,它的右尽头就是位置2,左尽头就是位置0。往后同理。
3-2代码
while(1) { read(n); ans=0; if(n==0) break; for(int i=1;i<=n;i++) read(a[i]); s.push(0); //我们先往栈内push一个位置0,方便后续计算。 s.push(1); for(int i=2;i<=n;i++) { ll lim=s.top(); while((s.size()!=1)&&a[i]<a[lim]) { s.pop(); ans=max(ans,a[lim]*((i-lim)+(lim-1-s.top()))); lim=s.top(); } s.push(i); } while(s.size()!=1) { ll lim=s.top(); s.pop(); ans=max(ans,((n+1-lim)+(lim-1-s.top()))*a[lim]); } printf("%lld\n",ans); }
这就是本题最终解。


