排序
1. 在多个数据元素(Ri)的序列,其中每个元素有相应的关键字(Ki)(也叫元素的属性),通过关键字的固有关系来对对应数据元素进行排序
2. 排序稳定性:元素R1 R2 的关键字K1 K2相同,排序前R1在R2前面,排序后 R1在R2前面,则该排序方法是稳定的。
3. 多关键字排序:排序先用最高优先级的关键字N1进行排序,,当N1关键字相同时使用N2优先级关键字进行排序,如果关键字还是相同依次使用N2,,Nn-1
4. 排序和交换两个重要手段
5. 排序选择要素:时间性能,空间性能,程序复杂度
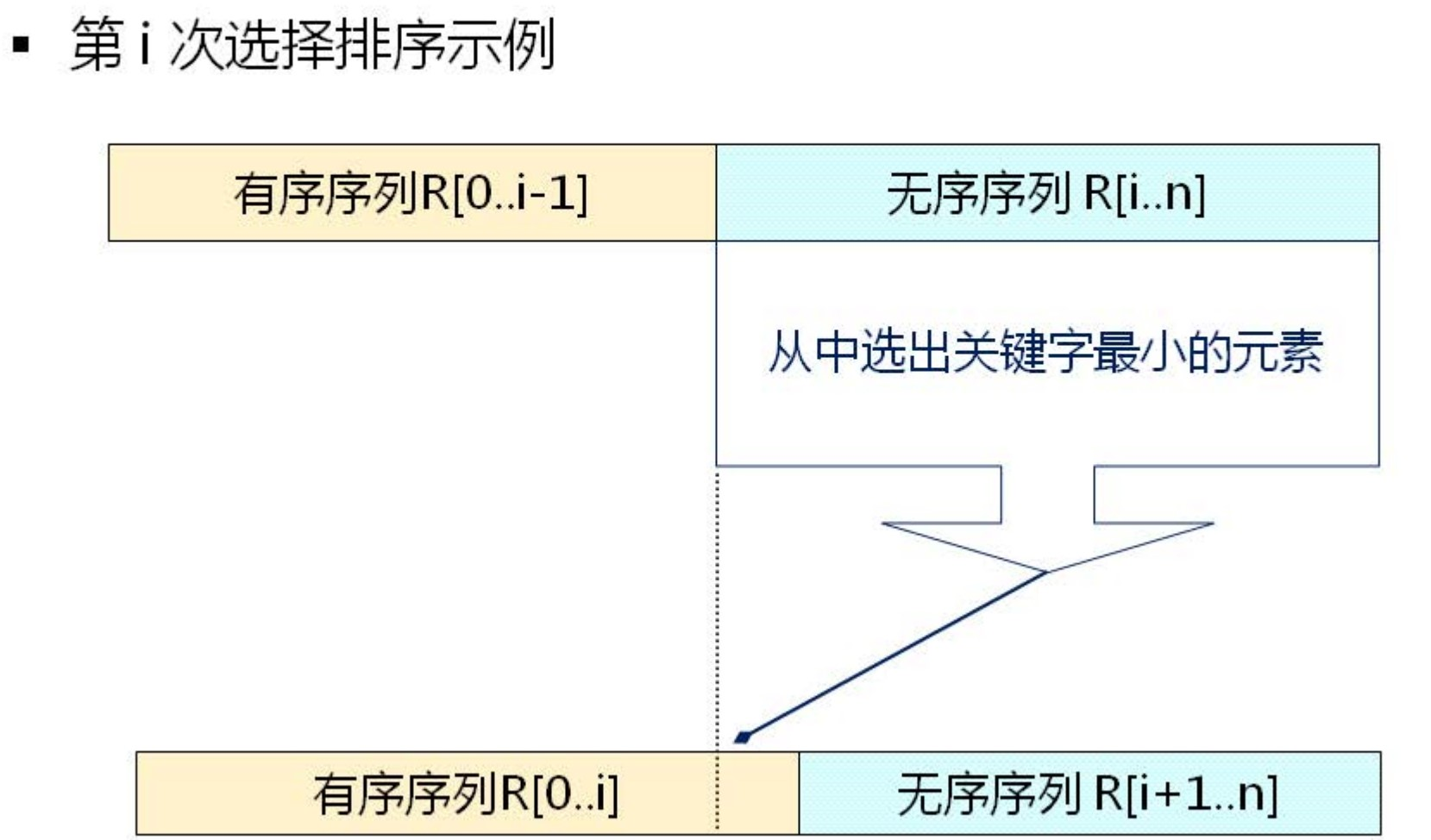
1.选择排序
思想:在排序到当前序列第 i 和元素时,从后面 n-i 个元素中选出最小元素,作为当前排序序列第 i 个元素。
code:
static void select(T array[], int len) { for(int x = 0; x < len; x++) { int min = x; for(int y = x + 1; y < len; y++) { if(array[min] > array[y]) //升序< 降序> min = y; } if(min != x) swap(array[x],array[min]); //不稳定排序 }
2.插入排序
思想:序列分为有序序列和无需序列。未排序序列选择第 i (1) 位的元素时,插入到前面的有序序列,使用 i 元素的关键字与前 i-1 个元素关键字进行比较,找到位置后插入即可

template <typename T>
static void insert_sort(T array[], int len, bool ascend = false)
{
for(int x = 1; x < len; x++)
{
int z = x;
T temp = array[z];
for(int y = x - 1; (y >= 0) && (ascend ? array[y] > temp: array[y] < temp); y--)
{
array[y + 1] = array[y]; //稳定排序
z = y;
}
if(z != x)
{
array[z] = temp;
}
}
}
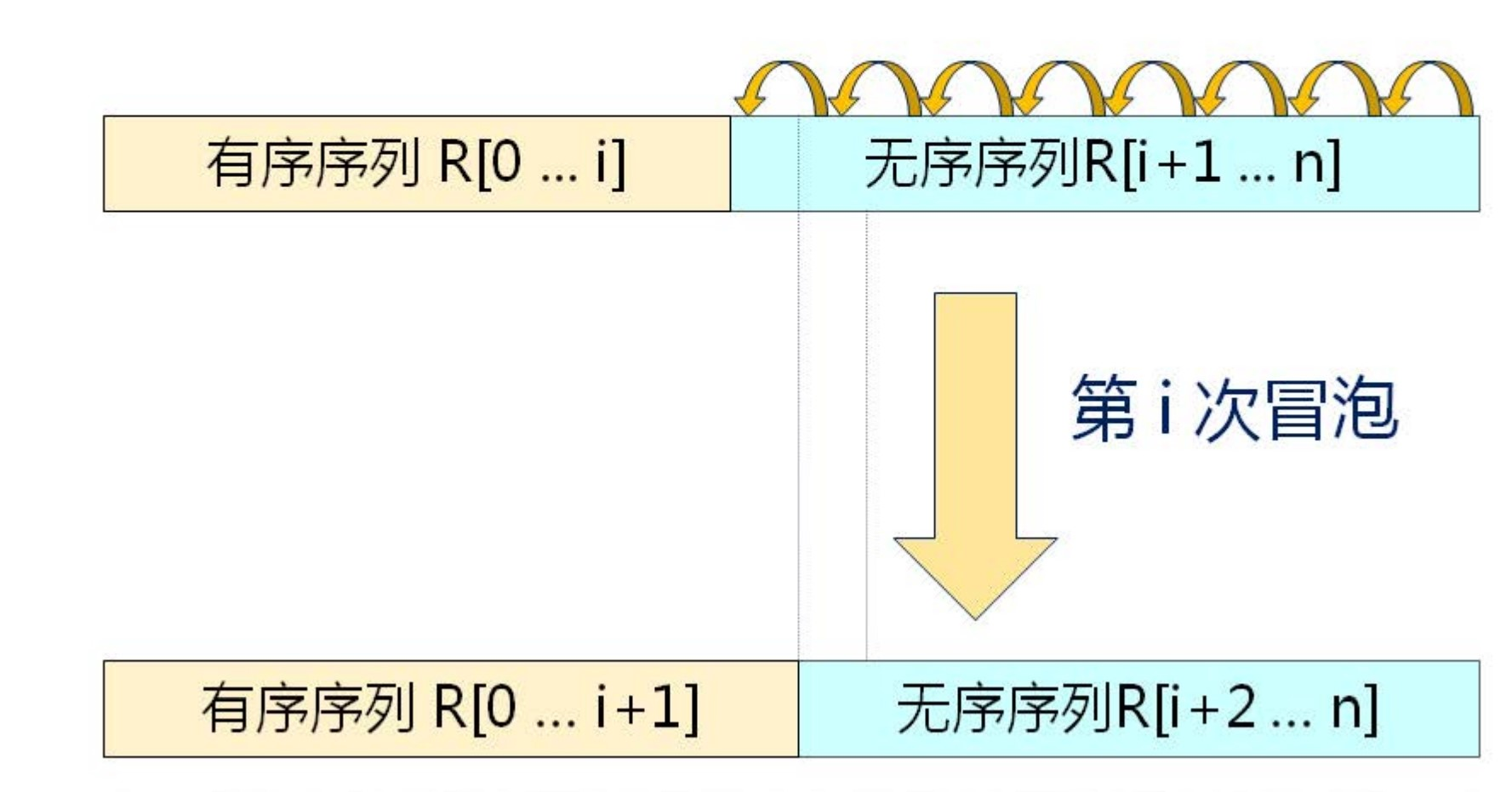
3.冒泡排序
思想:序列分为有序序列和无序序列,从整个序列的最后一个元素开始向前依次比较大小,小则比较数前移,大则用被比较的元素前移。
template <typename T>
static void bubble_sort(T array[], int len, bool ascend = false)
{
bool state = ture;
for(int x = 0; x < len && state; x++) //某个元素无法前的元素都是有序的,表明有序
{
state = false;
for(int y = len - 1; y > x; y--)
{
if(ascend ? array[y] > array[y - 1] : array[y] < array[y - 1])
{
swap(array[y],array[y - 1]);
state = ture;
}
}
}
}
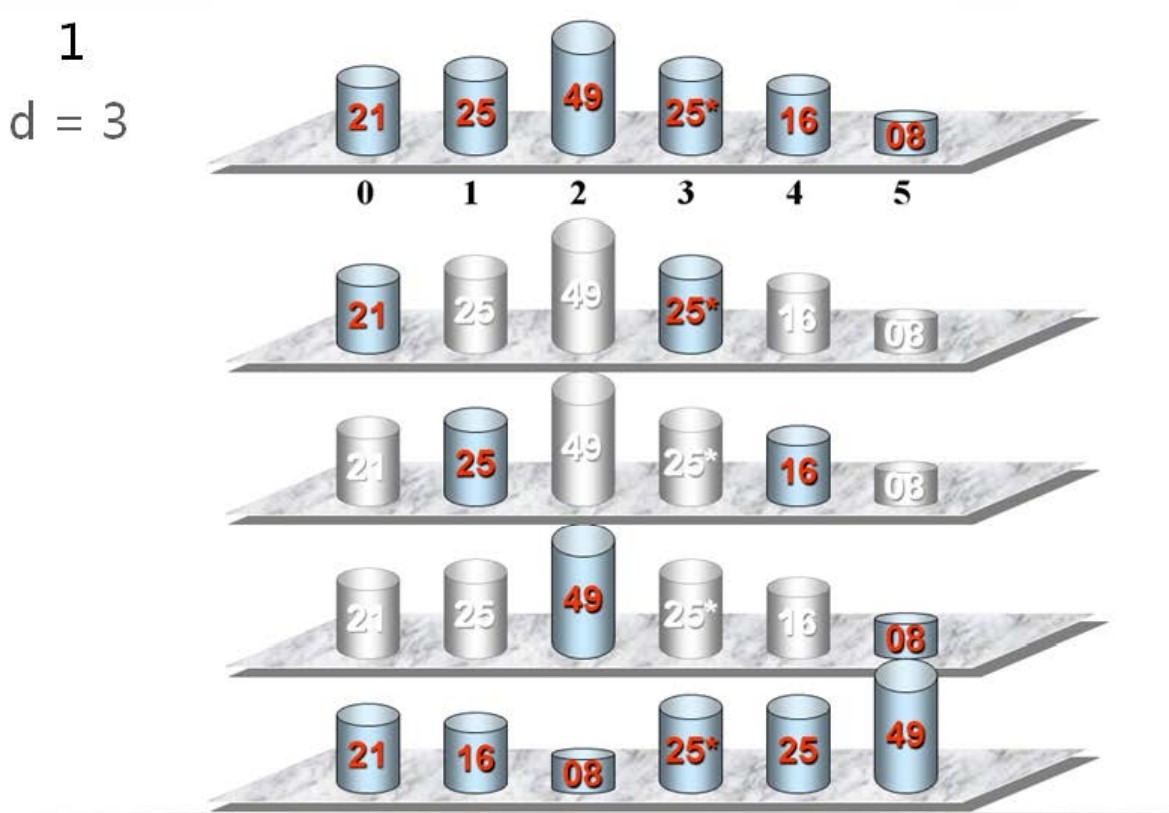
4.希尔排序
思想:将n个元素的序列分为d组,每一组使用插入排序。然后再分为d-1组,再分别排序。直到d=1。
如何分组: 将n个元素分为d个子序列:第一组:{R[1],R[1+d],R[1+2d]...R[1+kd]} 第二组:{R[2],R[2+d],R[2+2d]....R[2+kd]} .........第d组:{R[d],R[2d],R[3d]...R[(1+k)d]} 。
template <typename T>
static void shell_sort(T array[], int len, bool ascend = false)
{
int d = len;
do
{
d = d / 3 + 1; //???
for(int x = d ; x < len; x += d)
{
int z = x;
T temp = array[z];
for(int y = x - d; (y >= 0) && (ascend ? array[y] > temp: array[y] < temp); y -= d)
{
array[y + d] = array[y]; //稳定排序
z = y;
}
if(z != x)
{
array[z] = temp;
}
}
}
while(d > 1);
}
5.归并排序
思想:先将一个无序序列划分为两个无序序列,再将两个无序序列接着向下划分,直到每个子序列只包含一个元素此时每个子序列都是有序序列,
再两个两个子序列比较后合并,直到所有子序列合并为原来的序列,此时序列变为有序。
几个有序序列归并就叫几路归并。
稳定但是花费空间

template <typename T>
static void merge_sort(T array[], int len, bool ascned = ture)
{
T* temp_array = new T[len];
merge_sort_core(array, temp_array, 0, len - 1, ture);
delete[] temp_array;
}
template <typename T>
static void merge_sort_core(T array[], T temp_array[], int begin, int end, bool ascned = ture)
{
if(begin == end)
{
return;
}
else
{
// 分割
int mid = (begin + end) / 2;
merge_sort_core(array, temp_array, begin, mid, ascned);
merge_sort_core(array, temp_array, mid + 1, end, ascned);
// 合并
int x = begin, y = mid + 1, z = begin;
while(x <= mid && y <= end)
{
if(array[x] < array[y])
{
temp_array[z++] = array[x++];
}
else
{
temp_array[z++] = array[y++];
}
}
while(x <= mid)
{
temp_array[z++] = array[x++];
}
while(y <= end)
{
temp_array[z++] = array[y++];
}
for(z = begin; z <= end; z++)
{
array[z] = temp_array[z];
}
}
}
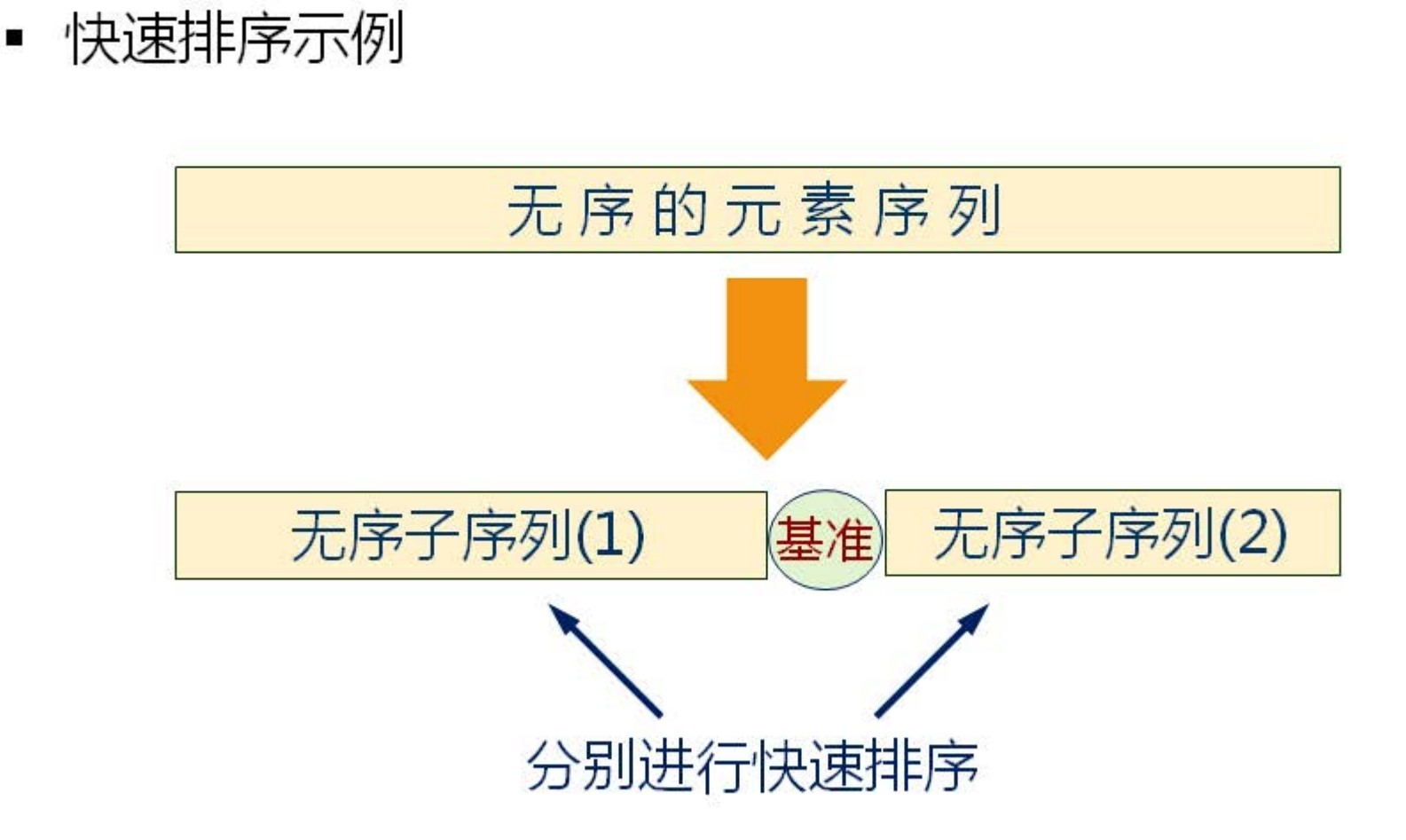
6.快速排序
思想: 通过在序列中选择一个基准值对一个无序序列划分,将无序序列大于基准值的放在左边,小于基准值的放在右边。再把左右两个子序列继续寻找基准值继续划分下去。
最后每个序列都只有一个元素,而此时整个序列变成有序的。
不稳定但是花费空间
template <typename T>
static void quick_sort(T array[], int len, bool ascned = ture)
{
quick_sort_core(array, 0, len - 1, ascned);
}
template <typename T>
static void quick_sort_core(T array[], int begin, int end, bool ascned = ture)
{
//确定基准值的位置
int base_pos = 0, base_value = array[begin], begin_slide = begin, end_slide = end;
while(begin_slide < end_slide)
{
while(begin_slide < end_slide && ascned ? base_value < array[end_slide] : base_value > array[end_slide])
{
--end_slide;
}
swap(array[begin_slide], array[end_slide]);
while(begin_slide < end_slide && ascned ? base_value >= array[begin_slide] : base_value <= array[begin_slide])
{
++begin_slide;
}
swap(array[begin_slide], array[end_slide]);
}
array[begin_slide] = base_value;
base_pos = begin_slide;
//继续划分
quick_sort_core(array, begin, (base_pos - 1), ascned);
quick_sort_core(array, base_pos + 1, end, ascned);
}





