树状数组快速入门

树状数组、 Fenwick Tree 或 Binary Indexed Tree ，通常用缩写 BIT 代表。

是一种 “一种基于二进制 lowbit ，用于维护（加法、位运算、max、gcd 的）前缀和的树形数组” 。

可以叫做 一个树状数组 或 一棵 Fenwick Tree 。

重要性质：同时满足即是数组又是树的性质。针对定义域时更多从数组角度，针对值域时更多从树角度。

1. lowbit

\(lowbit\) 定义域只在正整数上。

对于某个数正整数 \(x\) ，\(lowbit(x)\) 即 \(x\) 在二进制下最低位的 \(1\) 到最低位这一段。比如 \(110100\) 的 \(lowbit\) 是 \(100\) 。

1.1 lowbit 树图

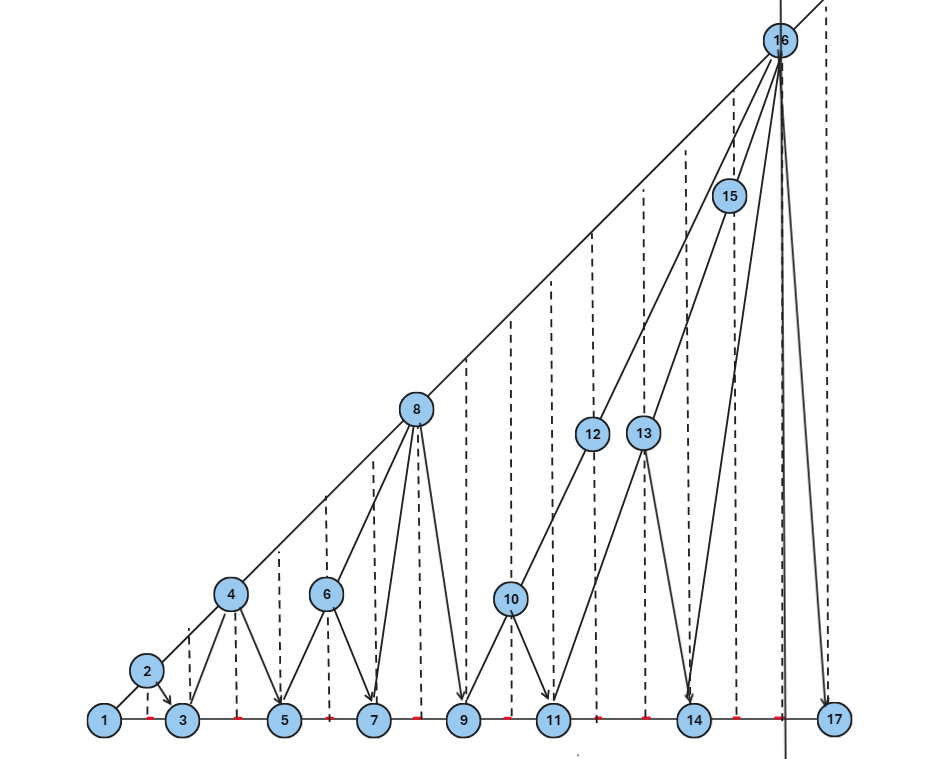
实线段是树边，是实际树图的边。

实箭头是前向边，由一棵子树的根节点连向右边一棵兄弟子树的左孙子。

一棵树最左侧的链是这棵树的左链。

所有 \(2^{x}\) 的点构成了树图的左链。

1.2. lowbit 递增链

对给定的值域 \(n\) ，\(x\) 的一条 \(lowbit\) 递增链即 \(x = x + lowbit(x)\ s.t.\ x \leq n\) 上的所有 \(x\) 。

对于 \(y = x + lowbit(x)\) ，\(y\) 在树图上是 \(x\) 的父亲。

\(x\) 最坏会按照 \(2\) 的幂次次增长，于是递增链长度是 \(O(\log n)\) 级别的。

1.3. lowbit 递减链

\(x\) 的一条 \(lowbit\) 递减链即 \(x = x - lowbit(x)\ s.t.\ x \geq 1\) 上的所有 \(x\) 。

对于 \(y = x - lowbit(x)\) 。

1. 若 \(x\) 在树图的左链上，则 \(y\) 是以 \(0\) 。
2. 若 \(x\) 不在树图的左链上，则 \(y\) 是它左边一颗兄弟子树。

以 \(x\) 为根的树最坏有 \(\log_2 x - 1\) 棵子树，于是递减链长度是 \(O(\log n)\) 级别的。

lowbit 递减链性质

让 \(x\) 的递减链访问到的所有节点为 \(y\) ，则以 \(y\) 为根的所有子树构成了 \(1 \sim x\) 。

1.4. 树状数组

\(c_{x}\) 即树上的节点，显然 \(c\) 数组构成了一颗树状结构。

对于 \(1 \sim n\) 上的数组 \(a\) ，长度为 \(n\) 的树状数组 \(c\) 用于维护前缀和数组 \(s\) 。

\(c_x\) 可以维护出若干 \(a_y\) 的贡献总和，即 \(x\) 的 lowbit 递减链上的 \(a_y\) 贡献总和。

1.4.1 树状数组维护的权值 c_x

详细的说，在树图上以 \(x\) 为根，\(\forall y\) 满足祖先或自己是 \(x\) 组成的集合为 \(S\) 。则 \(c_x\) 维护的就是集合 \(S\) 。

1.4.2 \(T = \sum_{i = 1}^{x} a_i\) 查询

根据树状数组权值 \(c_x\) 的意义， \(x\) 的子树加上所有左兄弟子树上的节点集合 \(M\) 即是 \(1 \sim x\) 。

在 lowbit 意义下， \(x\) 的 lowbit 递减链访问到的所有 \(y\) ，\(T = \sum c_y\) 。

1.4.3 \(a_x += k\) 单点加

根据树状数组 \(c_x\) 的意义，若执行 \(a_x += k\) 的单点加，则 \(x\) 的所有祖先 \(y\) 有 \(c_y += k\) 。

在 lowbit 意义下， \(x\) 的 lowbit 递增链访问到的所有 \(y\) ，只需维护 \(c_y += k\) 。

注意点：\(c_x\) 用以维护若干个 \(a_y\) 的贡献和，不意味只需要对 \(c\) 进行修改。一次修改需要同时修改 \(a\) 和 \(c\) 。

1.5 树状数组基础应用：“单点修改，前缀查询”

显而易见的只需要完成两个操作

1. 单点加：\(a_x += k\) 。（初始化也是单点加）
2. 前缀查：\(query\ \sum_{i = 1}^{x} a_i\)

http://oj.daimayuan.top/course/15/problem/634

1.6 树状数组基于高维差分应用：维护加法的“区间加，区间查询”

1.6.1 适用于可差分的运算规则：加法、异或

当维护的前缀和是加法前缀和时，可以利用加法的差分性质做到区间加，区间查询。

异或是二进制下的加法，显然也有差分性质。推导公式类似。

1.6.2 原理

我们可以快速对 \(a\) 单点加，前缀和查询。

如何快速对 \(a\) 区间加，前缀和查询？维护的元素不能变，依旧需要维护 \(s\) 。但可以对其他元素建树。

做法是不对 \(a\) 建树，而对 \(a\) 的差分数组 \(d\) 建树。然后借助树状数组，通过 \(d\) 维护 \(s\) 。

只需要 \(d_l += k, d_{r + 1} -= k\) 即可完成 \(a_{l \sim r} += k\) 。\(a\) 的前缀和 \(s\) 可以被维护。

接下来要做的只是让 \(s\) 可以被 \(d\) 表示。

\[\begin{aligned} s_x &= \sum_{i = 1}^{x} a_i \\ &= \sum_{i = 1}^{x} \sum_{j = 1}^{i} d_j \\ &= \sum_{i = 1}^{x} \sum_{j = 1}^{x} [j \leq i] d_j \\ &= \sum_{i = 1}^{x} \sum_{j = 1}^{x} [i \leq j] d_i \\ \textbf{交换指标}\\ &= \sum_{i = 1}^{x} d_i \sum_{j = 1}^{x} [j \geq i] \\ &= \sum_{i = 1}^{x} d_i (x - i + 1) \\ \textbf{分离 x}\\ &= (x + 1) \sum_{i = 1}^{x} d_i - \sum_{i = 1}^{x} i \times d_i \\ \end{aligned} \]

直接用差分数组初始化。

可以将两个树状数组封装进一个 BIT_PRO 中。

1.6.3 适用场景

https://www.luogu.com.cn/problem/P1438

https://codeforces.com/contest/1955/problem/E

http://oj.daimayuan.top/course/15/problem/687

基于差分维护 \(O(\log n)\) 的区间加和区间查，通常是树状数组一个比较鸡肋的功能。它的适用场景通常是异或转换成 01 串翻转形态。可以断言，任何 01 串翻转都可以用两颗树状数组无脑解决。

同样的，对定义域“单点修，前缀查”的朴素树状数组也是比较鸡肋的。树状数组的核心应用在于：对值域建树->权值树状数组->二维全偏序。

2. 权值树状数组/Fenwick Tree

一种常数和复杂度都非常优秀，快速维护前缀的数据结构。

适用场景为二维全偏序： \(i < j, a_i < a_j\) (小于号或大于号均可)。

需要注意： \(k < i < j, a_i < a_j\) 是二维偏序而非二维全偏序。

非全偏序下。若是加法偏序可以用 Fenwick Tree 处理。若 \([k, j]\) 满足窗口滑动可以用单调队列处理。否则只能用线段树处理。

2.1 应用一：Fenwick Tree 上b倍增

2.1.1 维护单点增删，查询最大的 \(T\) 满足 \(\sum_{i = 1}^{T} a_i \leq s\) 。

单点增删是 Fenwicik Tree 的基础操作。

查第 \(k\) 小，很容易想到在用 Fenwick Tree check 维护二分，时间复杂度为 \(O(\log^{2} n)\) 。

Fenwick Tree 支持查询：\(max\ T \ s.t.\ \sum_{i = 1}^{T} a_i \leq s\) 。

不考虑如何递增得到最大的 \(T\) 。显然 \(T\) 是固定的答案，只看答案。那么只需要找到一条快速路径从 \(1\) 到 \(T\) 。
树状数组是一棵树！快速路径显然是个经典倍增问题！时间复杂度为 \(O(\log n)\) 。

int find(T s) {
    int pos = 0;
    for (int i = LGN; ~i; --i) {
        if (pos + (1 << i) <= sz && (c[pos + (1 << i)] <= s) {
            pos += (1 << i);
            s -= c[pos];
        }
    }
    return pos;
}

http://oj.daimayuan.top/course/15/problem/636

2.1.2 维护单点增删，查询第 k 小。

当 Fenwick Tree 的点权全为 \(1\) 或 \(0\) ，倍增找到的终点不保证点权为 \(1\) ，但下一位的点权一定为 \(1\) 。第 \(k\) 小即查询 \(max\ T = \sum_{i = 1}^{T} a_i \leq k - 1\) 的 \(T + 1\) 。

查到 \(k - 1\) 的位置 \(T\) ，然后往后跳一步，即得到第 \(k\) 小的下标。

https://www.luogu.com.cn/problem/P1168

2.2 应用二：二维前缀偏序，加法意义二维偏序

二维前缀偏序问题可以：一维上单向扫描并单点修改。Fenwick Tree 维护偏序的前缀查询或区间修改，并在另一维上单向扫描。

2.2.1 逆序对

一维单向扫描单点修改，一维区间 cnt 。

https://www.luogu.com.cn/problem/P1908

2.2.2 LDIS

一维单向扫描单点修改，一维单向区间 max 。

https://acm.hdu.edu.cn/showproblem.php?pid=5256

2.2.3 扫描线，二维数点

裸扫描线，一维单向扫描单点触发 event ，一维单向查询 event 。

http://oj.daimayuan.top/course/15/problem/686

2.2.4 扫描线，区间不同数之和

扫描线做法，一维单向扫描单点触发 event ，一维单向查询 event 。

http://oj.daimayuan.top/course/15/problem/687

3. 高维树状数组

顾名思义是“利用树状数组维护数组 \(a\) 的高维前缀和 \(s\) ”。

与一维树状数组的代码几乎一模一样。

一般用处较少，但理解不难。在少数情况下可以避免写线段树套线段树。

http://oj.daimayuan.top/course/15/problem/637

3.1 基于加法差分的二维区间加与区间查询

同样的想办法让 \(s\) 被 \(d\) 维护，推公式：

\[\begin{aligned} s_{x, y} &= \sum_{i = 1}^{x} \sum_{j = 1}^{y} a_{i, j} \\ &= \sum_{i = 1}^{x} \sum_{j = 1}^{y} \sum_{l = 1}^{i} \sum_{k = 1}^{j} d_{l, k} \\ &= \sum_{i = 1}^{x} \sum_{l = 1}^{x} \sum_{j = 1}^{y} \sum_{k = 1}^{y} [l \leq i] [k \leq j] d_{l, k} \\ \textbf{交换指标}\\ &= \sum_{i = 1}^{x} \sum_{l = 1}^{x} \sum_{j = 1}^{y} \sum_{k = 1}^{y} [l \geq i] [k \geq j] d_{i, j} \\ &= \sum_{i = 1}^{x} \sum_{j = 1}^{y} d_{i, j} (x - i + 1) (y - j + 1) \\ \textbf{微笑展开……}\\ &= \sum_{i = 1}^{x} \sum_{j = 1}^{y} d_{i, j} (xy - xj -yi + x + y + ij - i - j + 1) \\ \textbf{分离 x，y}\\ &= \sum_{i = 1}^{x} \sum_{j = 1}^{y} \left ( (x + 1)(y + 1) - j(x + 1) - i(y + 1) + ij \right ) d_{i, j} \\ &= (x + 1) (y + 1)\sum_{i = 1}^{x} \sum_{j = 1}^{y} d_{i, j} - (x + 1) \sum_{i = 1}^{x} \sum_{j = 1}^{y} j d_{i, j} - (y + 1) \sum_{i = 1}^{x} \sum_{j = 1}^{y} i d_{i, j} + \sum_{i = 1}^{x} ij d_{i, j} \\ \end{aligned} \]

用二维差分初始化。

可以将四个树状数组封装进一个 BIT_2D_PRO 中。

https://loj.ac/p/135

4. 树状数组快速入门题解报告

https://www.cnblogs.com/zsxuan/p/18127506

5. 旅途的终点

1. 树状数组里一定要写 assert 。
2. 涉及离散化情况，务必记得坐标向右偏移一。
3. 树状数组只能解决二维前缀偏序和二维加法偏序，务必先确定是否真的可行。
4. \(dp_0 = 0\) 是不需要维护的 \(0\) 的，于是 Fenwick Tree 好维护前缀点权 max 。当维护点权 min ，做一个转化： \(a_i = limit - a_i + 1\) 插入 Fenwick Tree ，按 max 查。取出时 \(a_i = limit - a_i + 1\) 。离散化下的上限 \(limit = n + 1\) 即可。
5. 用树状数组的时候脑子要清醒，能推出公式。