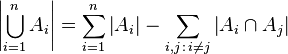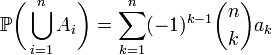数论总结（二）

Posted on 2017-05-04 16:51 蓝空阅读(252) 评论(0) 编辑收藏举报

（一）欧拉函数

用途：对正整数n，欧拉函数 $\varphi(n)$ 是小于或等于n的正整数中与n互质的数的数目。

通式：

,其中p1, p2……pn为x的所有质因数，x是不为0的整数。φ(1)=1（唯一和1互质的数(小于等于1)就是1本身）。 (注意：每种质因数只一个。比如12=2*2*3那么φ（12）=12*（1-1/2）*(1-1/3)=4

若n是质数p的k次幂，

，因为除了p的倍数外，其他数都跟n互质。

（二）欧拉定理

互质：若N个整数的最大公因数是1，则称这N个整数互质。

在数论中，欧拉定理,（也称费马-欧拉定理）是一个关于同余的性质。欧拉定理表明，若n,a为正整数，且n,a互质，则:

a^[φ(n)]≡1 （mod n）

其中： φ函数的值　通式：φ(x)=x(1-1/p1)(1-1/p2)(1-1/p3)(1-1/p4)…..(1-1/pn)，其中p1, p2……pn为x的所有质因数，x是不为0的整数。

φ(1)=1（唯一和1互质的数(小于等于1)就是1本身）。 (注意：每种质因数只一个。比如12=2*2*3那么φ（12）=12*（1-1/2）*(1-1/3)=4

证明

将1~n中与n互质的数按顺序排布：x1,x2……xφ(n) （显然，共有φ(n)个数）

我们考虑这么一些数：

m1=a*x1; m2=a*x2; m3=a*x3 …… mφ(n)=a*xφ(n)

1）这些数中的任意两个都不模n同余，因为如果有mS≡mR (mod n) （这里假定mS更大一些），就有：

mS-mR=a(xS-xR)=qn，即n能整除a(xS-xR)。但是a与n互质，a与n的最大公因子是1，而xS-xR<n，因而左式不可能被n整除。也就是说这些数中的任意两个都不模n同余，φ(n)个数有φ(n)种余数。

2）这些数除n的余数都与n互质，因为如果余数与n有公因子r，那么a*xi=pn+qr=r(……)，a*xi与n不互质，而这是不可能的。那么这些数除n的余数，都在x1,x2,x3……xφ(n)中，因为这是1~n中与n互质的所有数，而余数又小于n.

由1）和2）可知，数m1,m2,m3……mφ(n)（如果将其次序重新排列）必须相应地同余于x1,x2,x3……xφ(n).

故得出：m1*m2*m3……mφ(n)≡x1*x2*x3……xφ(n) (mod n)

或者说a^[φ(n)]*(x1*x2*x3……xφ(n))≡x1*x2*x3……xφ(n) （mod n）

( 公式：ａ＝ｂ（ｍｏｄ　ｎ）　＜＝＞　ａ＋ｃ＝ｂ＋ｃ（ｍｏｄ　ｎ）　

＜＝＞　ａ－ｂ＝0　（ｍｏｄ　ｎ）　)

或者为了方便：K{a^[φ(n)]-1}（mod n）≡0 这里K=x1*x2*x3……xφ(n)。

可知K{a^[φ(n)]-1}被n整除。但K中的因子x1,x2……都与n互质，所以K与n互质。那么a^[φ(n)]-1必须能被n整除，即a^[φ(n)]-1≡0 （mod n），即a^[φ(n)]≡1 （mod n），得证。

（三）费马小定理

a是不能被质数p整除的正整数，则有a^(p-1) ≡ 1 (mod p)

证明这个定理非常简单，由于p是质数，所以有φ(p) = p-1，代入欧拉定理即可证明。推论：对于任意正整数a，有a^p ≡ a (mod p)，因为a能被p整除时结论显然成立。

（四）费马大定理

n >2时，关于x, y, z的方程 x^n + y^n = z^n 没有正整数解。

（五）中国剩余定理

中国剩余定理（CRT）的表述如下

设正整数两两互素，则同余方程组

有整数解。并且在模下的解是唯一的，解为

其中，而为模的逆元。

int CRT(int a[],int m[],int n)
{
    int M = 1;
    int ans = 0;
    for(int i=1; i<=n; i++)
        M *= m[i];
    for(int i=1; i<=n; i++)
    {
        int x, y;
        int Mi = M / m[i];
        extend_Euclid(Mi, m[i], x, y);
        ans = (ans + Mi * x * a[i]) % M;
    }
    if(ans < 0) ans += M;
    return ans;
}

（六）鸽巢原理（抽屉原理）

鸽巢原理，又名狄利克雷抽屉原理、鸽笼原理。

其中一种简单的表述法为：

若有n个笼子和n+1只鸽子，所有的鸽子都被关在鸽笼里，那么至少有一个笼子有至少2只鸽子。

另一种为：

若有n个笼子和kn+1只鸽子，所有的鸽子都被关在鸽笼里，那么至少有一个笼子有至少k+1只鸽子。

如果要把n个物件分配到m个容器中，必有至少一个容器容纳至少⌈n / m⌉个物件。（⌈x⌉大于等于x的最小的整数）

（七）容斥原理

容斥原理又称排容原理，在组合数学里，其说明若 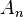$A_1$ , ..., $A_n$ 为有限集，则

\left|\bigcup_{i=1}^n A_i\right|=\sum_{i=1}^n\left|A_i\right|-\sum_{i,j\,:\,i\neq j}\left|A_i\cap A_j\right|

+\sum_{i,j,k\,:\,i\neq j\neq k}\left|A_i\cap A_j\cap A_k\right|-\ \cdots\cdots\ \pm \left|A_1\cap\cdots\cap A_n\right|

其中 $|A|$ 表示 $A$ 的基数。例如在两个集的情况时，我们可以透过将 $|A|$ 和 $|B|$ 相加，再减去其交集的基数，而得到其并集的基数。

也可以写成：

\mathbb{P}\biggl(\bigcup_{i=1}^n A_i\biggr) =\sum_{k=1}^n (-1)^{k-1}\sum_{\scriptstyle I\subset\{1,\ldots,n\}\atop\scriptstyle|I|=k} \mathbb{P}(A_I),

特殊情况：

如果在容斥原理的概率形式中，交集A_I的概率只与I中元素的个数有关，也就是说，对于{1, ..., n}中的每一个k，都存在一个a_k，使得：

a_k=\mathbb{P}(A_I)

，对于每一个

I\subset\{1,\ldots,n\} \,\, (|I|=k),

则以上的公式可以简化为：

\mathbb{P}\biggl(\bigcup_{i=1}^n A_i\biggr) =\sum_{k=1}^n (-1)^{k-1}\binom nk a_k

（八）欧几里得

欧几里德算法又称辗转相除法，用于计算两个整数a,b的最大公约数。

基本算法：设a=qb+r，其中a，b，q，r都是整数，则gcd(a,b)=gcd(b,r)，即gcd(a,b)=gcd(b,a%b)。

int gcd(int a,int b)
{
    return b ? gcd(b,a%b) : a;
}

（九）扩展欧几里得

基本算法：对于不完全为 0 的非负整数 a，b，gcd（a，b）表示 a，b 的最大公约数，必然存在整数对 x，y ，使得 gcd（a，b）=ax+by。

证明：设 a>b。

　　1，显然当 b=0，gcd（a，b）=a。此时 x=1，y=0；

　　2，ab!=0 时

　　设 ax1+by1=gcd(a,b);

　　bx2+(a mod b)y2=gcd(b,a mod b);

　　根据朴素的欧几里德原理有 gcd(a,b)=gcd(b,a mod b);

　　则:ax1+by1=bx2+(a mod b)y2;

　　即:ax1+by1=bx2+(a-(a/b)*b)y2=ay2+bx2-(a/b)*by2;

　　根据恒等定理得：x1=y2; y1=x2-(a/b)*y2;

这样我们就得到了求解 x1,y1 的方法：x1，y1 的值基于 x2，y2.

　上面的思想是以递归定义的，因为 gcd 不断的递归求解一定会有个时候 b=0，所以递归可以结束。

代码实现：

递归：

int exgcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    int r=exgcd(b,a%b,x,y);
    int t=x;
    x=y;
    y=t-a/b*y;
    return r;
}

非递归：

int exgcd(int m,int n,int &x,int &y)
{
    int x1,y1,x0,y0;
    x0=1; y0=0;
    x1=0; y1=1;
    x=0; y=1;
    int r=m%n;
    int q=(m-r)/n;
    while(r)
    {
        x=x0-q*x1; y=y0-q*y1;
        x0=x1; y0=y1;
        x1=x; y1=y;
        m=n; n=r; r=m%n;
        q=(m-r)/n;
    }
    return n;
}

扩展欧几里德算法的应用主要有以下三方面：

（1）求解不定方程；

（2）求解模线性方程（线性同余方程）；

（3）求解模的逆元；

（1）使用扩展欧几里德算法解决不定方程的办法：

对于不定整数方程ax+by=c，若 c mod Gcd(p, q)=0,则该方程存在整数解，否则不存在整数解。
上面已经列出找一个整数解的方法，在找到a * x+ b * y = Gcd(a, b)的一组解x0,y0后，a * x+ b * y = Gcd(a, b)的其他整数解满足：
x' = x0 + b/Gcd(a, b) * t
y' = y0 - a/Gcd(a, b) * t (其中t为任意整数) (也就是无数个解）
至于ax+by=c的整数解，只需将a * x+ b * y = Gcd(a, b)的每个解乘上 c/Gcd(a, b) 即可。

在找到a*x+ b*y = Gcd(a, b)的一组解x0,y0后，应该是得到ax+by=c 的一组解为：

x'' = x0*(c/Gcd(a,b)),

y'' = y0*(c/Gcd(a,b))

ax+by=c的其他整数解满足：

x= x'' + b/Gcd(a, b) * t

y= y'' - a/Gcd(a, b) * t (其中t为任意整数)

p 、q就是p * a+q * b = c的所有整数解。

最小正整数解应该是设distance= b/Gcd(a, b) (x两个相邻解的最小距离）

则xx=(x0%distance+distance)%distance (当然x0改成x也是一样的，因为有取余，下面的模线性方程组同理)

用扩展欧几里得算法解不定方程ax+by=c;

代码如下：

int exgcd(int a,int b,int &x,int &y)  
{  
    if(b==0)  
    {  
        x=1;  
        y=0;  
        return a;  
    }  
    int r=exgcd(b,a%b,x,y);  
    int t=x;  
    x=y;  
    y=t-a/b*y;  
    return r;  
}  
  
bool linear_equation(int a,int b,int c,int &x,int &y)  
{  
    int d=exgcd(a,b,x,y); ///d是gcd(a,b);  
    if(c%d)  
        return false;  ///无解  
    int k=c/d;  
    x*=k; y*=k;        ///求得的只是其中一组解 也就是上面的x'',y''!!!  
    return true;  
}

模线性方程组定理概述：

定理一：设d = gcd(a, n), 假定对整数x', y', 有d = ax' + ny'，如果d | b, 则方程ax = b(mod)有一个解的值为x0, 满足：、

　　　　　　x0 = x'(b / d)(mod n）

　　定理二：假设方程ax = b(mod n)有解， x0是方程的任意一个解，则方程对模n恰有d个不同的解，分别为： xi = x0 + i * (n / d), 其中 i = 1,2,3......d - 1

(2)用扩展欧几里德算法求解模线性方程的方法：

同余方程 ax≡b (mod n)对于未知数 x 有解，当且仅当 gcd(a,n) | b（|表示整除）。且方程有解时，方程有gcd(a,n)个解。（这里由于规定同于方程组的解是同余类的个数，也就是在模m的一组完全剩余系中解的个数，术语有点多，还是有点懵！！！）

求解方程 ax≡b (mod n) 相当于求解方程 ax+ny=b, (x, y为整数)

设 d= gcd(a,n)，假如整数 x 和 y，满足 d= ax+ ny(用扩展欧几里德得出)。如果 d|b，则方程

a* x0+ n* y0= d，方程两边乘以 b/ d，(因为 d|b，所以能够整除)，得到 a* x0* b/ d+ n* y0* b/ d= b。
所以 x= x0* b/ d，

y= y0* b/ d 为 ax+ ny= b 的一个解，所以 x= x0* b/ d 为 ax=b (mod n ) 的解。

ax≡b (mod n)的一个解为 x0= x*(b/d)mod n，且方程的 d 个解分别为 xi= (x0+i*(n/d))mod n {i= 0... d-1}。

设s=n/d;

方程ax≡b (mod n)的最小正整数解为：(x%s+s)%s; 其中x为ax+by=b的解

（十一）高斯消元

（十二）莫比乌斯

（十三）线性同余

刷新页面返回顶部

Sweety

导航

公告