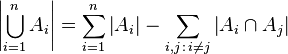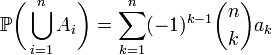Sweety

Practice makes perfect

导航

数论总结帖

Posted on 2016-05-13 20:41  蓝空  阅读(118)  评论(0)  编辑  收藏  举报

欧拉函数：

用途：对正整数n，欧拉函数\varphi(n)是小于或等于n的正整数中与n互质的数的数目。

通式：
  
,其中p1, p2……pn为x的所有质因数，x是不为0的整数。φ(1)=1（唯一和1互质的数(小于等于1)就是1本身）。 (注意：每种质因数只一个。比如12=2*2*3那么φ（12）=12*（1-1/2）*(1-1/3)=4
若n是质数p的k次幂，
  
，因为除了p的倍数外，其他数都跟n互质。

中国剩余定理  


鸽巢原理（抽屉原理）：

鸽巢原理，又名狄利克雷抽屉原理、鸽笼原理。

其中一种简单的表述法为：

   若有n个笼子和n+1只鸽子，所有的鸽子都被关在鸽笼里，那么至少有一个笼子有至少2只鸽子。

另一种为：

   若有n个笼子和kn+1只鸽子，所有的鸽子都被关在鸽笼里，那么至少有一个笼子有至少k+1只鸽子。

如果要把n个物件分配到m个容器中，必有至少一个容器容纳至少⌈n / m⌉个物件。（⌈x⌉大于等于x的最小的整数）

容斥原理：

容斥原理又称排容原理，在组合数学里，其说明若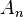A_1, ..., A_n 为有限集，则

\left|\bigcup_{i=1}^n A_i\right|=\sum_{i=1}^n\left|A_i\right|-\sum_{i,j\,:\,i\neq j}\left|A_i\cap A_j\right|+\sum_{i,j,k\,:\,i\neq j\neq k}\left|A_i\cap A_j\cap A_k\right|-\ \cdots\cdots\ \pm \left|A_1\cap\cdots\cap A_n\right|

其中|A|表示A的基数。例如在两个集的情况时，我们可以透过将|A|和|B|相加，再减去其交集的基数，而得到其并集的基数。

也可以写成：

\mathbb{P}\biggl(\bigcup_{i=1}^n A_i\biggr) =\sum_{k=1}^n (-1)^{k-1}\sum_{\scriptstyle I\subset\{1,\ldots,n\}\atop\scriptstyle|I|=k} \mathbb{P}(A_I),

特殊情况：

如果在容斥原理的概率形式中，交集AI的概率只与I中元素的个数有关，也就是说，对于{1, ..., n}中的每一个k，都存在一个ak，使得：

a_k=\mathbb{P}(A_I)，对于每一个 I\subset\{1,\ldots,n\} \,\, (|I|=k),

则以上的公式可以简化为：

\mathbb{P}\biggl(\bigcup_{i=1}^n A_i\biggr) =\sum_{k=1}^n (-1)^{k-1}\binom nk a_k



欧几里得：


扩展欧几里得：


莫比乌斯：


线性同余：